Mixture-of-Recursions:混合递归模型，通过学习动态递归深度，以实现对自适应Token级计算的有效适配

一、背景

Transformer 架构的问题：

• 对所有token进行统一计算(Uniform compute for all tokens)：每个token，无论多么简单或复杂，都要经过整个堆栈层 - 导致简单token的计算浪费，而较难token的利用率不足。
• 参数数量过多(Excessive parameter count)：Transformer 为每一层分配单独的权重，导致模型规模过大，并使训练和部署资源密集。
• 推理效率低下(Inefficient inference)：token不能提前退出，导致解码过程中不必要的计算和增加延迟——即使某些token已经“完成”。
• KV 缓存内存瓶颈(KV cache memory bottleneck)：所有层的所有 token 都存储键值对，这会快速消耗 GPU 内存并限制长上下文的使用。
• 缺乏潜在推理(Lack of latent reasoning)：没有对token表示进行迭代细化的机制；Transformers 依赖于单次前向传递，而没有内部推理循环。
• 固定计算预算(Fixed computational budget)：没有内置灵活性来在训练或推理期间动态调整计算 ，无论输入的复杂性或token的重要性如何。
• 没有测试时间适应性(No test-time adaptability)：标准 Transformer 无法在推理时调整深度或动态计算，除非进行重新训练或架构破解。

这促使研究者们寻找替代性的“高效”设计。在众多效率维度中，参数效率以及自适应计算是当前前景广阔且被广泛研究的方向。

• 参数效率（parameter efficiency）：即减少或共享模型权重。实现参数效率的一个有效方法是层权重绑定（layer tying），即在多个层间重复使用同一组共享权重。
• 自适应计算（adaptive computation）：即仅在需要时才投入更多计算资源。对于自适应计算，常见的方法是早退机制（early-exiting），该机制动态分配计算资源：让那些预测更简单的token更早退出网络。

尽管在这两个效率维度上分别取得了进展，但仍然缺乏一种能够有效统一参数效率和自适应计算的架构。

二、Mixture-of-Recursions简介

2.1 什么是MoR

混合递归（Mixture-of-Recursions, MoR）框架，该框架充分挖掘了递归Transformer的潜力，如下图：

混合递归 (MoR) 概览

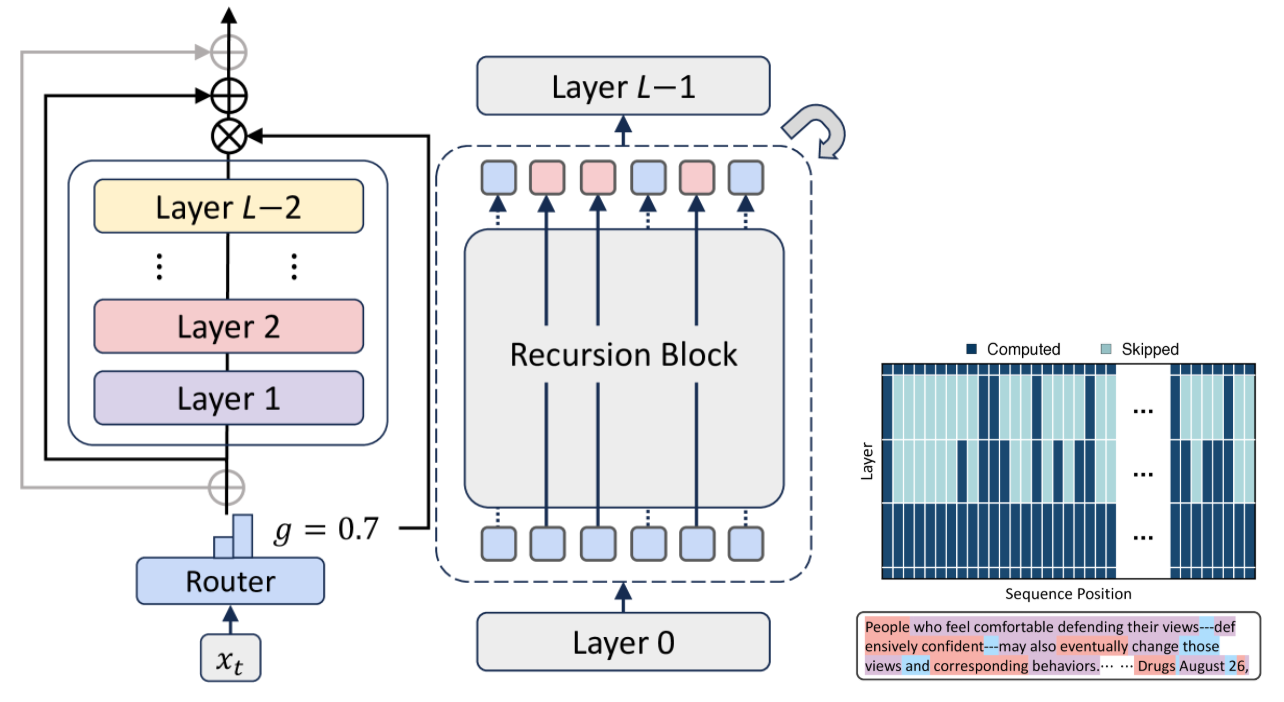
（左）每个递归步骤包含固定层堆栈和决定token是否继续递归的路由器（中间灰框区域）。（中）完整模型结构，其中共享递归步骤根据路由决策对每个token最多应用次。（右）展示token级递归深度的路由模式示例，颜色越深表示该token在递归块中的计算越活跃。底部数字以不同颜色标注各文本token的递归步数：1步(紫色)、2步(蓝色)和3步(橘色) 。

• MoR端到端地训练轻量级路由器（routers），为每个token分配特定的递归深度：路由器根据token所需的“思考深度”决定共享参数块应作用于该token的次数，从而将计算资源精准导向最需要的地方。

• 动态的token级递归（token-level recursion）天然支持递归层面的键值缓存，即有选择地存储和检索与每个token实际分配到的递归深度相对应的键值对。

• 目标导向的缓存策略（targeted caching strategy） 显著减少了内存开销，从而在不依赖后期（post-hoc）修改的情况下提升了吞吐量。

因此，MoR在单一架构内同时实现了三重效率提升：

• 通过共享权重压缩参数量
• 路由token以减少冗余浮点运算（redundant FLOPs）
• 递归式缓存键值以减少内存开销。

从概念上讲，MoR提供了一个用于隐空间思考（latent space reasoning）的预训练框架——通过迭代应用单个参数块来执行非语言式的思考（non-verbal thinking）。然而，与那些在生成前对增强的连续提示进行深思熟虑（deliberate）的方法不同，MoR直接在解码每个token的过程中实现这种隐空间思考（latent thinking）。

此外，其路由机制促进了模型纵向（沿深度轴 depth axis）的自适应推理（这种思考沿深度轴进行，类似于在序列水平轴 horizontal sequence axis 上生成连续想法），超越了先前工作中常见的统一、固定思考深度。

本质上，MoR使模型能够根据每个token的需求高效调整其思考深度，从而将参数效率与自适应计算统一起来。

2.2 论文贡献

• 统一的语言建模高效框架：本文提出了混合递归（Mixture-of-Recursions, MoR），这是首个在单一框架内统一多种效率范式的架构——参数共享、token级自适应思考深度和内存高效的键值缓存。
• 动态递归路由：本文引入了一个从头开始训练的路由，用于分配动态的token级递归深度。这确保了训练与推理行为的一致性，并消除了传统早退方法中所需的、成本高昂且损害性能的后置路由阶段（post-hoc routing stages）。
• 广泛的实证验证：在同等计算预算下，针对从1.35亿到17亿参数（此为基模型大小，MoR模型因参数共享拥有更少的唯一参数）的模型范围进行实验，结果表明：MoR通过改进验证损失和少样本准确率，相对于原始Transformer和递归基线模型，建立了一个新的帕累托边界（Pareto frontier）。
• 高效架构：MoR通过有选择地仅让必需序列参与注意力运算，显著降低了训练FLOPs。同时，键值缓存大小的减少带来了推理吞吐量本身的提升，而持续的深度级批量处理又进一步放大了这一提升效果。

三、MoR实现方法

3.1 预备知识

3.1.1 递归Transformer (Recursive Transformers)

标准Transformer通过堆叠个唯一的层来构建token表示，每个层包含一个自注意力机制 (self-attention) 和一个前馈网络 (feed-forward network)。在时间步，隐藏状态的演化过程为：其中 and 表示第层的参数。

递归Transformer（Recursive Transformers）旨在通过跨深度重用层来减少参数量。它们不再拥有组不同的权重，而是将模型划分为递归块，每个块使用共享的参数池，这种设计允许增加计算量（通过增加有效网络深度）而不增加参数量。

3.1.2 参数共享策略 (Parameter-sharing strategies)

本文研究了四种参数共享策略：

• 循环 (Cycle)
• 序列 (Sequence)
• 中周期 (Middle-Cycle)
• 中序列 (Middle-Sequence)

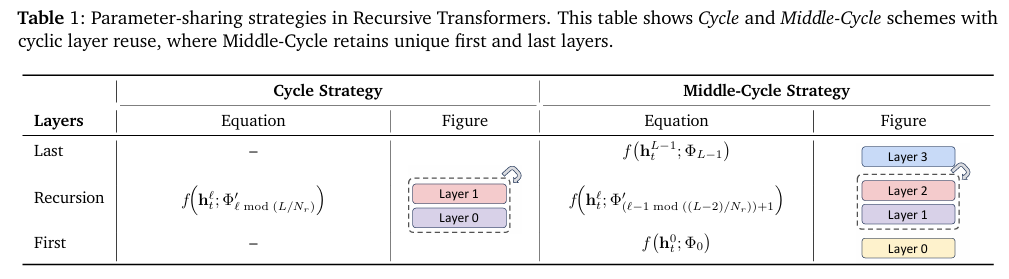
在 Cycle 共享中，递归块被循环重用。例如，考虑一个原始的非递归模型有，其递归对应版本使用次递归。在“Cycle”策略下，层被共享并展开为[]。在Sequence共享中，每个递归块在移动到下一个块之前连续重用相同的层，对于相同的配置会导致[]。两者在展开时具有相同的有效层数()，但顺序不同。Middle变体保留首层和末层(和)的完整容量参数，而在中间层之间共享权重。

3.1.3 增强递归模型的训练和推理效率

参数共享策略可以将唯一可训练参数的数量减少为递归次数的因子，从而有效分摊模型的内存占用。从分布式训练的角度来看，在使用全分片数据并行 (Fully Sharded Data Parallel, FSDP)时，这变得非常高效。

虽然单个 all-gather 操作以前只支持一次迭代（即 1 次迭代/收集），但递归模型在所有递归步骤中重用相同的已收集参数（即次迭代/收集）。

此外，递归架构支持一种新颖的推理范式——连续深度级批处理 (continuous depth-wise batching)。该技术允许处于不同阶段的token被分组到单个批次中，因为它们都使用相同的参数块。这可以消除气泡 (bubbles)——即等待其他样本完成所花费的空闲时间——从而带来显著的吞吐量提升。

3.1.4 先前研究的局限性

尽管模型参数被绑定，但通常为每个深度使用不同的键值缓存。这种设计未能减少缓存大小，意味着高检索延迟 仍然是一个严重的推理瓶颈。

此外，大多数现有的递归模型只是对所有token应用固定的递归深度，忽略了其变化的复杂性。虽然像早退机制这样的后处理 方法可以引入一些自适应性，但它们通常需要单独的训练阶段，这可能会降低性能 。

理想情况下，递归深度应该在预训练期间动态学习，使模型能够以数据驱动的方式适应每个token的难度来调整其计算路径。然而，这样的动态路径引入了一个新挑战：退出的token在后续递归深度上将缺少键值对。

解决这个问题需要一种并行解码机制来高效计算实际的键值对，但这需要单独且复杂的工程，并使系统复杂化。

3.2 混合递归 (Mixture-of-Recursions)

混合递归 (MoR)——一个在预训练和推理过程中动态调整每个 token 递归步长的框架。MoR 的核心在于两个组件：

• 路由机制，它分配特定于 token 的递归步长，以便自适应地将计算集中在更具挑战性的 token 上；
• KV缓存策略，它定义了键值对如何存储并在每个递归步骤中有选择地用于注意力机制。

3.2.1 路由策略：专家选择 vs. token选择

• 专家选择路由 (Expert-choice routing)

  

  Expert-choice routing

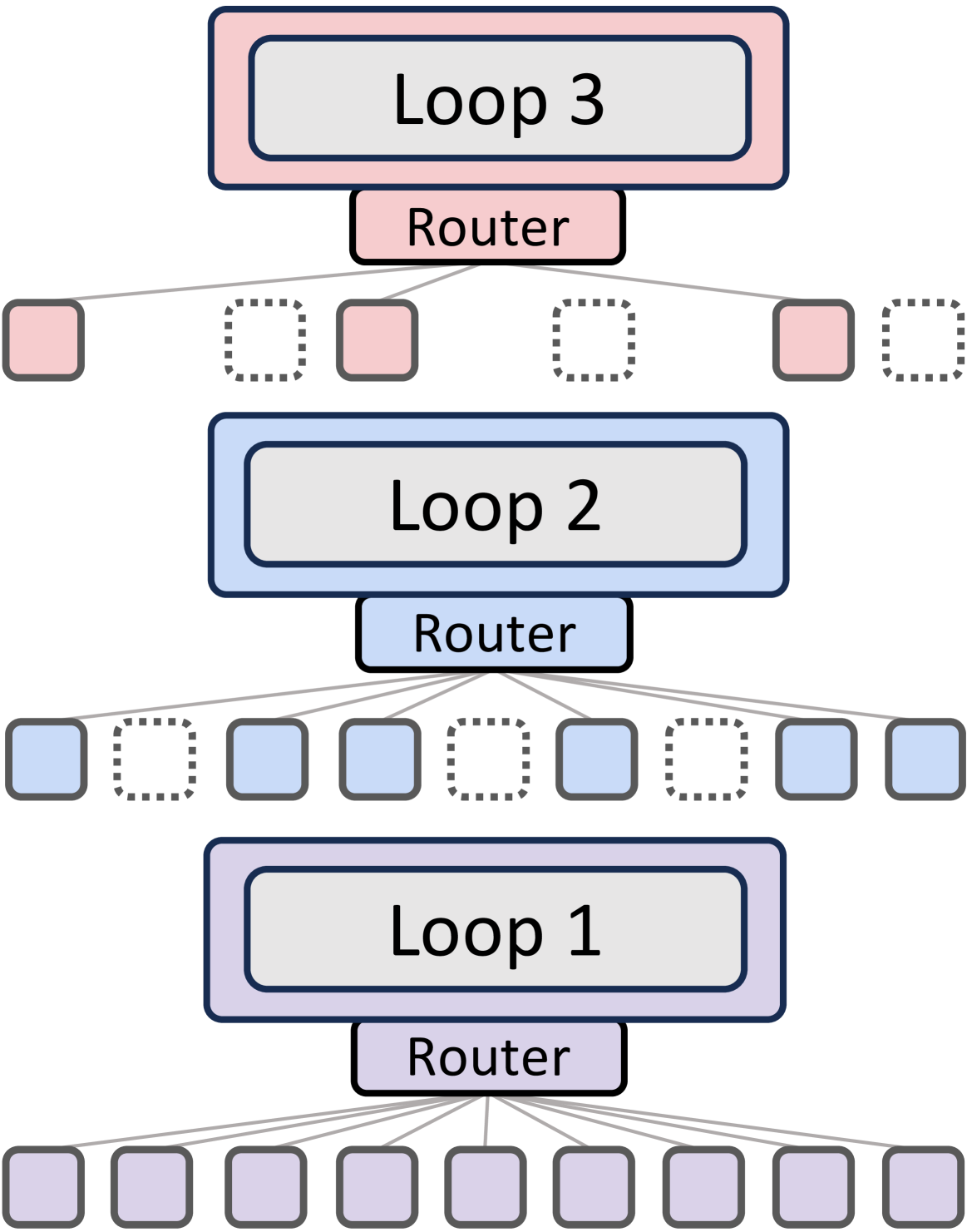
  受 MoD (Mixture-of-Depths) 模型中 top-k门控机制 (top-k gating) 的启发，在专家选择路由中，每个递归深度成为一个专家并选择其偏好的 top-k 个token（例如，对于，本文有三个专家：专家1应用第一次递归步骤，专家2应用第二次递归步骤，依此类推）。在每个递归步骤，相应的路由使用隐藏状态（输入到第个递归块的隐藏状态）及其路由参数来计算token 的标量分数。这里，表示一个激活函数，如 sigmoid 或 tanh。然后，选择 top-k 个token通过递归块：
  

  其中是递归步骤上所有分数的 百分位阈值。

  为了确保步骤间的连贯推进，本文采用分层过滤：只有在递归步骤被选中的token才能在步骤被重新评估。这模拟了提前退出行为，同时是从头开始学习的。随着更深的层倾向于编码越来越抽象和稀疏的信息 ，该机制优先计算仅针对需求最高的token。

• Token选择路由（Token-choice routing）

  

  Token-choice routing

  与专家选择（expert-choice）（在每一步递归中筛选token）不同，token选择从一开始就将每个token分配给完整的递归块序列。形式化地说，给定隐藏状态(在Middle-Cycle策略下，)路由对专家执行非线性函数（softmax 或 sigmoid）：，其中表示专家的路由分数。Token被分配给专家(Top-1门控)，这对应于顺序应用递归次。随后，隐藏状态按以下方式递归更新：

  在同等计算量下比较路由策略，本文将专家选择的token分配预算与token选择对齐。

  为了评估两种路由方式，需要限制两种路由方式的总计算量相同。考虑在负载均衡绝对平均的情况下，每个token被分配到不同深度的概率是相同的且为，因此第个循环块在负载绝对平均的情况下处理的token数量可以被表示为。例如当的时候，循环块1处理3/3的token，循环块2处理2/3的数据，循环块3处理1/3的数据。专家选择路由也采用了这种方案即每经过一个循环块则少处理，k 按序列N_r$, , 在 个递归步骤中分配。

• 优势与局限（Strengths and limitations）

  

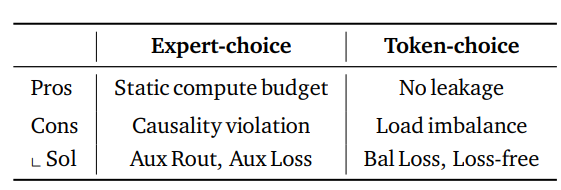
  尽管专家选择路由通过静态 top-k 筛选保证了完美负载均衡，但它存在信息泄露问题。这种训练期间的因果性违背迫使本文采用辅助路由器或正则化损失，旨在推理时精确检测 top-k tokens而无需访问未来token信息。

  与此同时，token选择虽无此类泄露问题，但由于其固有的负载均衡挑战，通常需要平衡损失或无损失算法.

3.2.2 KV 缓存策略：递归式缓存 vs. 递归共享

动态深度模型在自回归解码期间常面临 KV 缓存一致性问题。当一个token提前退出时，其在更深层的对应键和值将缺失，而这可能对后续token至关重要。现有方法尝试复用陈旧条目或运行并行解码，但这些方案仍会引入额外开销和复杂性。为此，本文设计并探索了两种专为 MoR 模型定制的 KV 缓存策略：递归式缓存（recursion-wise caching）与递归共享（recursive sharing）。

• 递归式缓存（recursion-wise caching）

  

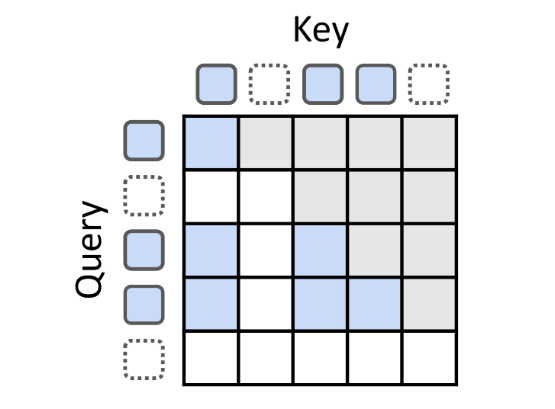
  本文有选择地缓存键值对:仅被路由到特定递归步骤的tokens在该层级存储其键值条目。因此，每个递归深度的 KV 缓存大小由专家选择中的容量因子精确决定，或根据token选择中的实际均衡比例确定。

  注意力计算随后被限制在这些本地缓存的tokens上。这一设计促进了块本地计算，提升了内存效率并减少了 I/O 需求。

• 递归共享（recursive sharing）

  

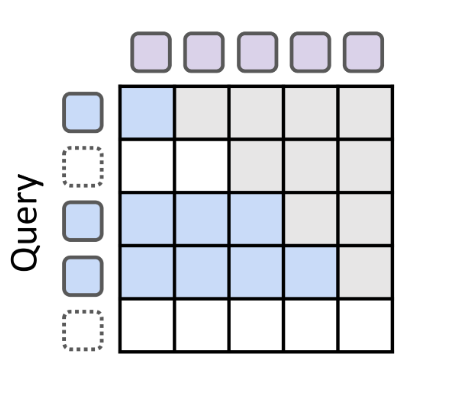
  MoR 模型的关键设计选择是：所有tokens至少经过第一个递归块。利用这一点，仅在初始步骤缓存 KV 对，并在所有后续递归中复用它们。因此，查询长度）可能随递归深度增加而缩短（基于选择容量），但键和值长度将始终保持完整序列。这确保了所有tokens无需重新计算即可访问历史上下文，尽管存在分布不匹配.

• 优势与局限（Strengths and limitations）

  

  Recursion-wise caching将整个模型的 KV 内存和 I/O削减至约 倍（假设容量因子遵循序列, , 分布，经过个递归步骤）。它还将每层注意力 FLOPs降至普通模型的倍（其中为上下文长度)，从而显著提升训练和推理阶段的效率。与此同时，递归共享（recursive sharing）通过全局复用上下文可实现最大内存节省。具体而言，跳过共享深度的 KV 投影和预填充操作可带来显著的加速。然而，注意力 FLOPs仅按因子减少，且大量的 KV I/O仍会导致解码瓶颈。

四、Experiments

4.1 主要结果 (Main Results)

在 16.5e18 FLOPs 的同等训练计算预算下，本文的混合递归 (Mixture-of-Recursions, MoR) 模型与普通 Transformer (Vanilla Transformer) 和递归 Transformer进行了比较。

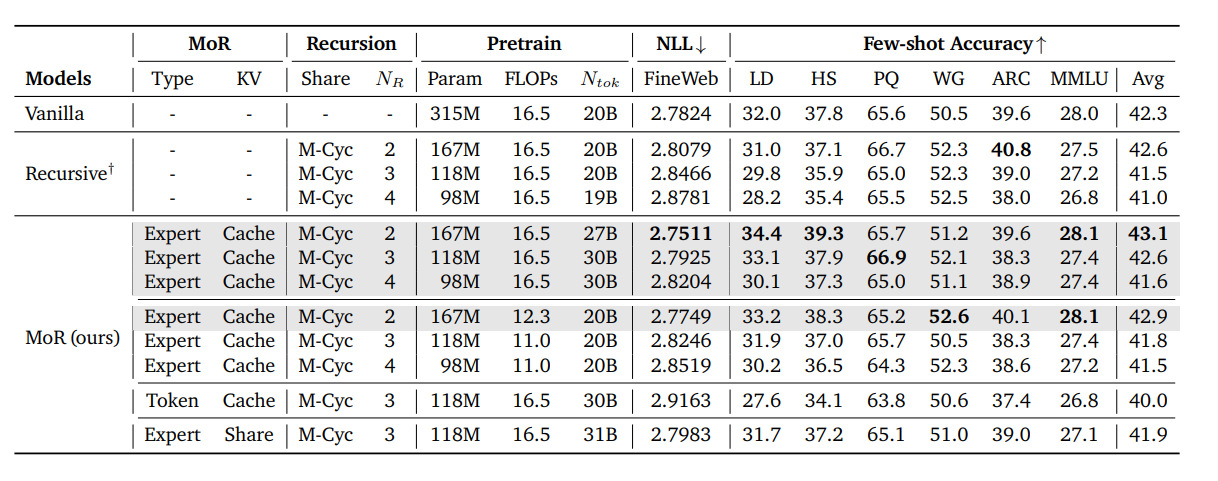
在相同的训练计算量下，MoR（Mixture-of-Recursions）模型的参数更少，性能优于baseline。在相同的训练数据量下（20B tokens），MoR模型使用的计算量更少，性能优于baseline。MoR的性能会随着路由和缓存策略的不同而变化，expert-choice routing优于 token-choice routing。按循环缓存(recursion-wise caching)性能优于循环共享(recursive sharing)，但循环共享(recursive sharing)显存需求更低。

4.2 等计算量分析 (IsoFLOP Analysis)

四个规模（four scales）上进行了实验——1.35亿（135M）、3.6亿（360M）、7.3亿（730M）和 17亿（1.7B）参数——将递归模型和 MoR 配置的递归次数固定为三（），导致唯一参数量大约仅为普通模型的三分之一。每个模型在三个 FLOPs 预算下进行预训练：2e18、5e18 和 16.5e18。

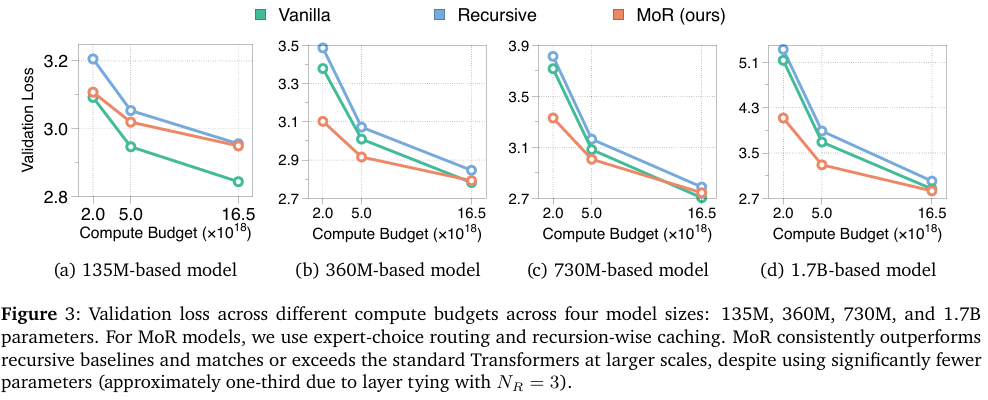
这些结果突显了 MoR 是标准 Transformer 的一种可扩展且高效的替代方案。它以显著降低的参数量实现了强大的验证性能，使其成为预训练和大规模部署）的有力候选者。

4.3 推理吞吐量评估 (Inference Throughput Evaluation)

这一部分进行了推理阶段的吞吐量分析，这里又提到了recursive transformer才能使用的continuous depth-wise batching，这一技术留到下一篇文章解读。本文测试了在16.5e18 FLOPs预算下训练的，360M参数规模的MoR模型的吞吐量，这些模型的递归深度分别为2、3和4。如下图最左，B是batch大小，整体来讲增加递归深度会导致更多标记提前退出，并进一步减少键值（KV）缓存的使用。这反过来又显著提升了吞吐量（例如，MoR-4在B = Max时实现了高达2.06倍的速度提升）。

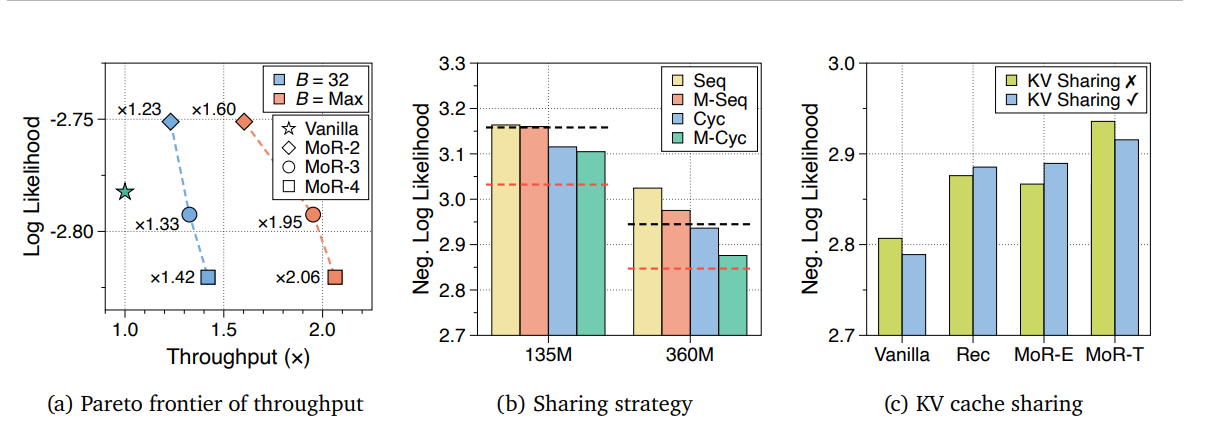
五、Ablation Studies

5.1 参数共享策略 (Parameter Sharing Strategies)

参数共享 是递归 Transformer 和 MoR 的关键组成部分。

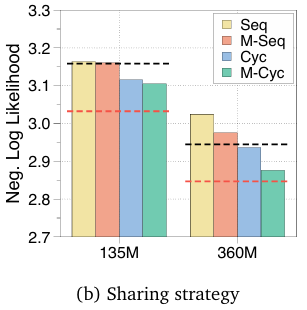
如图所示，Middle-Cycle策略始终实现最低的验证损失。续展示的所有 MoR 和递归 Transformer 中均采用Middle-Cycle配置。

5.2 路由策略 (Routing Strategies)

MoR 框架中专家选择和 token选择路由方案的各种设计选择的影响进行了广泛的消融研究。

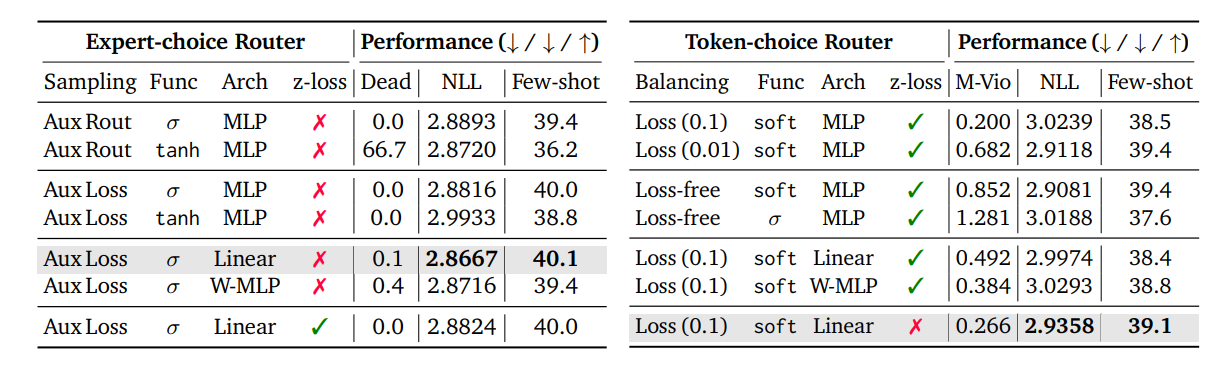
• 专家选择路由
  • 使用辅助损失 对于推理时行为比训练一个独立的辅助路由器更有效。
  • sigmoid 标准化函数和简单的线性路由器架构带来最佳性能。
  • 辅助 z 损失对准确率的影响可以忽略不计，尽管它确实略微降低了死token比例。
• token选择路由
  • 采用 MLP 路由器的 Softmax 激活表现最好
  • 而移除 z 损失反而带来更高的性能和路由稳定性

5.3 KV 缓存策略 (KV Caching Strategies)

即使在参数共享架构中，KV 共享也能稳健工作

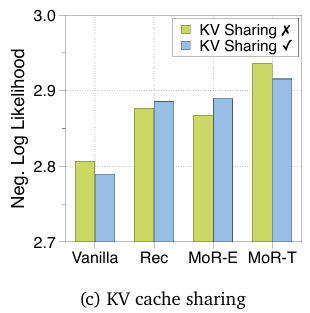
递归 Transformer（Recursive Transformer） 尽管其自由度减少，对 KV 共享却保持了相对稳健。共享参数 的深度之间表现出高度一致的幅值模式 和高余弦相似度，这为KV 共享仅导致轻微性能下降 提供了明确的理由。

虽然递归 KV 共享具有减少内存占用和 总计算量减少（overall FLOPs）的优势，但它在固定token数设置下会导致专家选择路由 的性能大幅下降。这表明仅更新和关注在该递归深度活跃的token可能更为有益。相反，采用token选择路由的 MoR 则可以从 KV 共享中受益，其较弱且不准确的路由决策以通过 共享 KV 对提供的额外上下文信息 得到补充。

六、Analysis

6.1 计算最优缩放分析 (Compute-optimal Scaling Analysis)

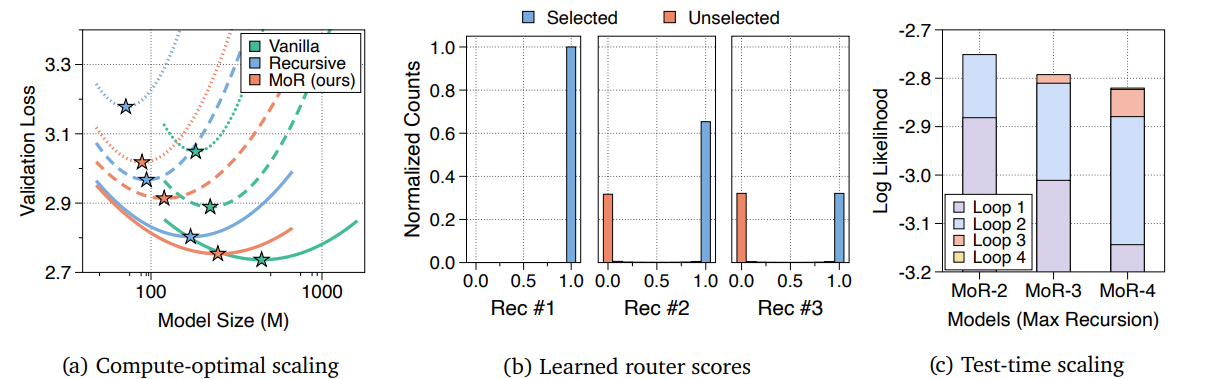
如图所示，在等计算量约束下，与基线模型相比，MoR 展现出独特的计算最优缩放行为。

MoR 最优路径的更大斜率（即更接近零）表明，它从增加参数量中获益更显著（即数据需求更低）。这可能是因为共享参数块本身的性能变得尤为重要，甚至比输入更多数据更重要。

因此，MoR 模型的最优缩放策略倾向于将资源分配给通过使用更大模型进行更短步数的训练来增加模型容量。

6.2 路由分析 (Routing Analysis)

递归深度的分配反映了token的语义重要性

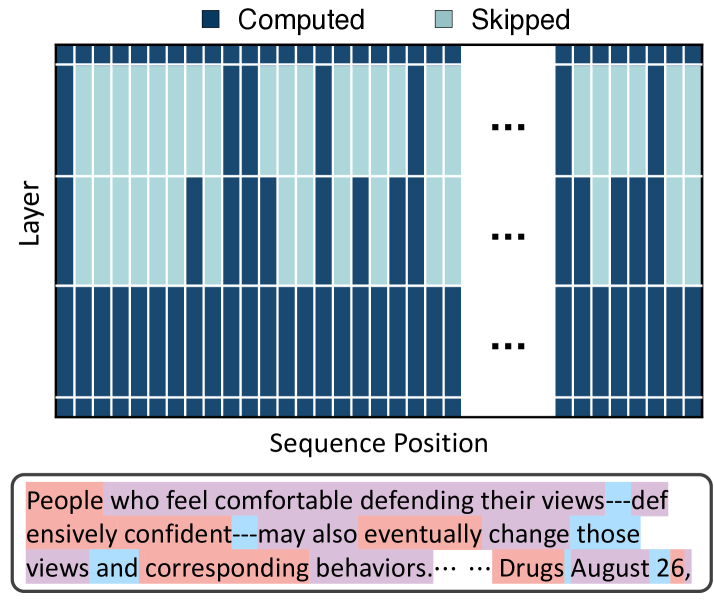
如图展示了一个token特定递归深度的定性示例。第一个token“People”或富含内容的token如“-ensively confident”和“Drugs”经过三个递归步骤，而功能词如“and”、“---”和“∖n”则经过两个步骤。

相比之下，中等语义重要性的token通常仅经历一次递归。这种模式表明，递归深度的分配与每个token的语义重要性紧密对应。

带辅助损失的专家选择路由器完美区分了选中与未选中的tokens

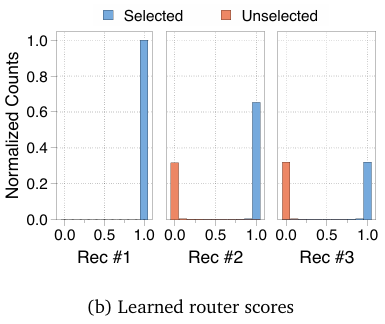
每个递归步骤的专家选择路由器输出分布。对于每个递归步骤，绘制了路由分数的归一化计数，区分了被专家选中的token（蓝色）和未被选中的token（橙色）。在所有步骤中，辅助损失在路由器输出中实现了完美分离，被选中的token高度集中在接近 1.0 的路由分数附近，而未选中的token则聚集在接近 0.0 的附近。

6.3 测试时缩放分析 (Test-time Scaling Analysis)

MoR 通过更深递归实现测试时缩放

在图中可视化了在 的 MoR 模型中，对数似然（log-likelihood）如何随递归步骤演变。叠加的条形图展示了当token的最大思考（递归）深度逐渐增加时，每个模型的性能。这表明，更深的递归不仅提供了额外的计算资源，还使得每个后续步骤能够进一步专注于在其特定深度精炼token表示或“思考过程”，从而带来更好的性能。

因此，这些结果支持了 MoR 支持测试时缩放的观点：在推理时分配更多的递归步骤可以提高生成质量。

七、总结

7.1 局限性与未来工作

• 推理型 MoR 模型 (Reasoning MoR models)

  最近的研究强调了推理链中的冗余性，并通过应用token级自适应计算（如早退机制（early-exit mechanisms））来解决它 。

  本文的 MoR 框架通过自适应地确定单个token所需的递归深度，内在地支持隐式推理。

  因此，一个关键的未来工作涉及探索当在实际的推理数据集上进行后训练（post-trained）时，路由器（router）如何动态学习调整以适应思维链（chain-of-thought, CoT）的需求。

  开发显式将递归深度与推理复杂度对齐的高级路由策略可能会提升推理准确率、计算效率甚至可解释性。

• 进一步扩展模型家族 (Further scaling model family)

  由于计算限制，实验仅限于参数规模最高达 17亿的模型。自然的下一步是在更大规模和更大的语料库上训练 MoR 模型。

  为了降低总体预训练成本，也可以探索持续预训练，从现有的预训练普通大语言模型检查点开始。

  本文计划研究使用递归模型的各种初始化策略的 MoR 性能。此外，为了确保公平的可扩展性比较，需要考虑递归 Transformer 在为早退而进行的后训练期间可能出现的性能下降，并将普通 Transformer 的推理吞吐量约束纳入考量。

• 自适应容量控制 (Adaptive capacity control)

  专家选择路由具有通过预定义的容量因子保证完美负载均衡的显著优势。然而，当本文在推理时希望分配不同的容量时，就出现了一个限制。

  具体来说，在本文的 MoR 模型中，观察到当使用辅助损失时，被选中和未被选中token的路由器输出几乎是完美分离的。这使得在训练后调整 top-k 值变得困难。因此，需要一种更具适应性的模型设计，能够在训练和推理阶段利用不同的容量，以解决这一限制。

• 与稀疏算法的兼容性 (Compatibility with sparse algorithms)

  鉴于 MoR 的token级自适应递归，本文可以通过集成结构化稀疏性进一步优化计算。这种方法允许有选择地激活子网络或参数，在token和层级别动态剪枝不必要的计算。这种对稀疏模型设计的探索有望带来显著的效率提升。

  作者相信许多基于稀疏性的技术，如剪枝或量化，与 MoR 高度互补。这将为递归模型内有效的稀疏架构提供更深入的见解，为未来研究指明有前景的方向。

• 扩展到多模态和非文本领域 (Expansion to multimodal and non-text domains)

  MoR 的递归块本质上是模态无关的，使其自适应深度机制能够扩展到文本处理之外。这一关键特性使 MoR 能够轻松集成到视觉、语音和统一的多模态 Transformer 架构中。

  将token自适应递归应用于长上下文视频或音频流，有潜力实现更高的内存效率和显著的吞吐量提升，这对实际应用至关重要。通过动态调整每个token或片段的处理深度，MoR 可以释放这些显著的优势。

Reference

1. DMixture-of-Recursions: Learning Dynamic Recursive Depths for Adaptive Token-Level Computation
2. Mixture-of-Recursions(GitHub)
3. Mixture-of-Recursions: 混合递归模型，通过学习动态递归深度，以实现对自适应Token级计算的有效适配
4. Transformer终结者！谷歌DeepMind全新MoR架构问世，新一代魔王来了
5. 条件计算系列2：Mixture-of-Recursions Learning Dynamic Recursive Depths for Adaptive Token-Level Computation
6. Google’s Mixture Of Recursions : End of Transformers
7. Mixture of Recursions in Deep Learning — how it outperforms transformers using fewer parameters