Muon An optimizer for hidden layers in neural networks
一、引言
在深度学习领域,优化算法对模型训练效率和性能起着关键作用。从经典的随机梯度下降 (SGD) 及其动量法,到自适应优化方法 Adam/AdamW 等,一系列优化器大大加速了神经网络的收敛。
Muon (Momentum Orthogonalized by Newton-Schulz):一种新的神经网络优化器。Muon 因其出色的实用性能而备受关注:它曾创下 NanoGPT 的速度纪录。Muon是一种利用牛顿–舒尔茨迭代对梯度动量进行正交化处理的优化算法。Muon优化器专门针对神经网络隐藏层的二维权重参数设计,其核心思想是在每次参数更新前,对梯度更新矩阵进行近似正交化处理,从而改善优化动力学。
Muon 的原理:利用牛顿–舒尔茨迭代高效地逼近梯度矩阵的正交化形式,并将其用于更新神经网络中的二维权重参数,从而加速训练收敛。且并不只是在Adam基础上的“小打小闹”,而是体现了关于向量与矩阵差异的一些值得深思的原理。
二、Muon设计与实现
Muon 优化器的设计初衷是针对神经网络中的线性变换层(即权重为矩阵的层,例如全连接层、卷积层等)提供一种专门优化方案。传统优化器(如 SGD 或 Adam)对所有参数一视同仁地应用统一的更新规则,而 Muon 采取了一种模块化的视角:根据层类型的不同采用不同的优化策略,以充分利用每类层结构的特性。这种“为不同网络模块定制优化器”的理念正是深度学习优化最新趋势的一部分。Muon 优化器聚焦于二维权重矩阵参数(例如全连接层的权重矩阵或卷积核张量展平后的矩阵),通过对这些矩阵形式的梯度更新进行特殊处理,以提升优化效果。

2.1 Muon 定义
Muon 是针对神经网络隐藏层二维参数的优化器。其算法定义如下:

- 梯度计算与动量累积:在每次参数更新迭代t t,首先计算当前参数 θt − 1 的梯度 Gt = ∇θℒt(θt − 1)。然后将其累积到动量矩阵Bt中,即Bt ← μBt − 1 + Gt,其中μ是动量超参数(类似于SGD动量法中的动量因子)。初始化时B0 = 0
- 上述伪代码(Algorithm 2 Muon)展示了Muon优化算法的主要循环步骤,其中Bt表示动量梯度累积,μ是动量系数,η是学习率。在每次迭代中,先计算梯度Gt并累积到动量矩阵Bt中,然后对Bt执行Newton-Schulz迭代(即步骤5的Ot ← NewtonSchulz5(Bt)),最后用得到的正交化更新Ot对参数进行梯度下降更新(步骤6)
其中,‘NewtonSchulz5’被定义为以下 Newton-Schulz 矩阵迭代
1 | |
2.2 Muon 推导
Muon更新规则是:
这里msign是矩阵符号函数,它并不是简单地对矩阵每个分量取sign操作,而是sign函数的矩阵化推广。
SGD-momentum 和 Adam 对基于 Transformer 的神经网络中的二维参数产生的更新通常具有非常高的条件数。也就是说,它们几乎是低秩矩阵,所有神经元的更新仅由少数几个方向主导。我们推测,正交化有效地增加了其他“稀有方向”的规模,这些方向在更新中幅度较小,但对学习仍然很重要。
SVD很容易理解(即计算更新的USV⊤分解, 然后用UV⊤替换更新),但它太慢了。
如果每一步都对B做SVD来求解msign(B)的话,那么计算成本还是比较大的,因此作者提出了用Newton-schulz迭代来近似计算msign(B)。
假设n ≥ m,然后考虑在B⊤B = I处泰勒展开(B⊤B)−1/2,展开的方式是直接将标量函数t−1/2的结果用到矩阵中:
保留到二阶,结果是(15 − 10t + 3t2)/8,那么我们有
假如Xt是msign(B)的某个近似,我们认为将它代入上式后,会得到msign(B)的一个更好的近似,于是我们得到一个可用的迭代格式
考虑一般的迭代过程,令Xt = USV⊤
一般来说,如果我们定义五次多项式 φ(x) = ax + bx3 + cx5,那么应用系数为(a, b, c)的N步NS迭代将产生输出UφN(S)V⊤,其中φN(S)表示对构成S对角线的奇异值逐元素应用φ N次。
因此,为了保证 NS 迭代收敛到UV⊤需要做的就是:
- 确保S的初始项位于范围[0, 1]内
- 选择系数,使得对于所有x ∈ [0, 1],φN(x) → 1, N → ∞
为了满足第一个条件,只需
为了满足φN(x) → 1, N → ∞的要求,我们有一定的自由度,因为具有此属性的(a, b, c)有很多可能的选择。稍后我们将优化这个选择,但现在我们在下图中展示了简单的基线(a, b, c) = (2, −1.5.0.5)已经可以正常工作。
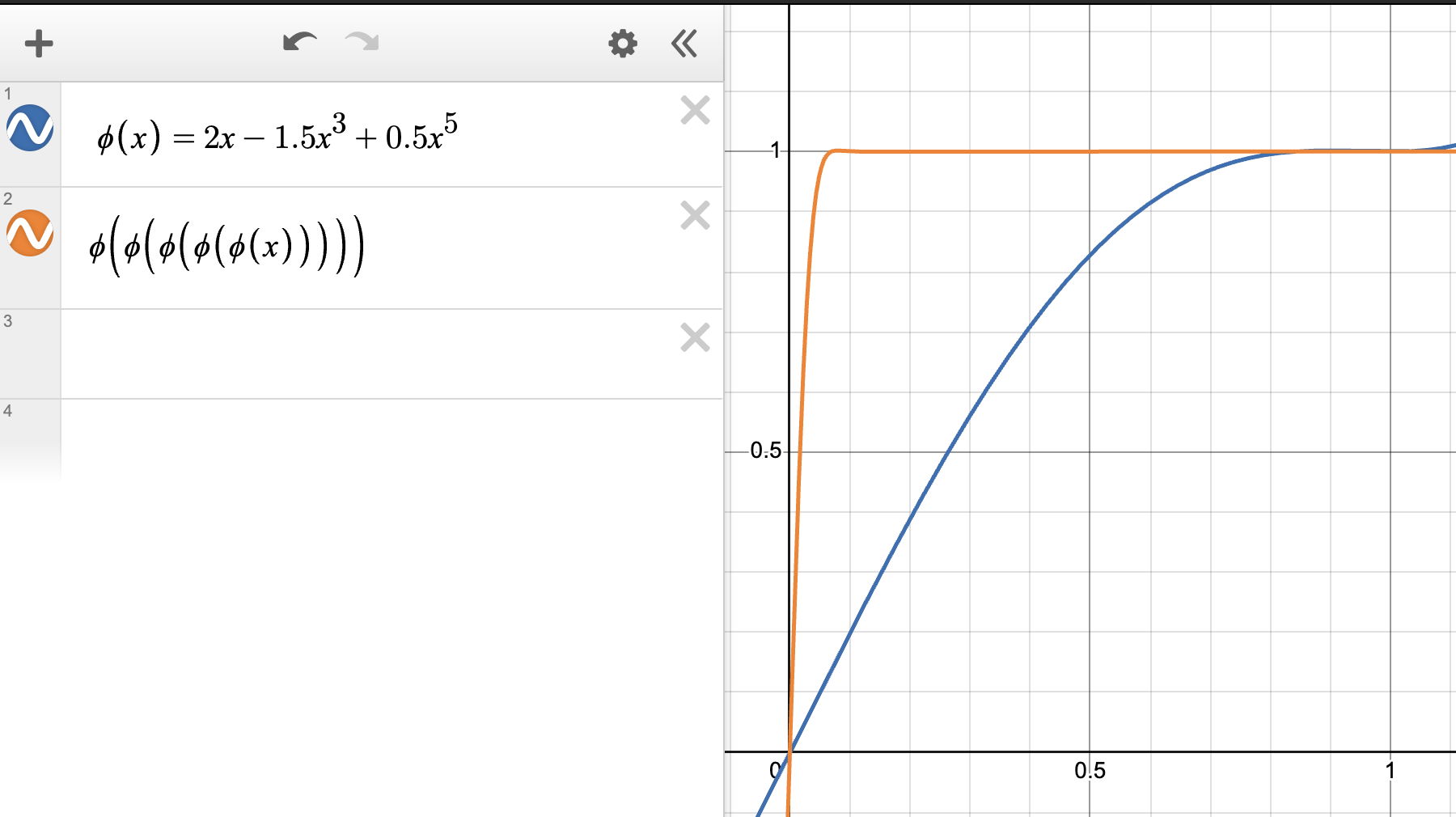
2.2.1 调整系数
尽管 NS 系数(a, b, c) = (2, −1.5.0.5)对于正交化更新来说表现得非常好,但可以进一步调整它们以减少我们需要运行的 NS 迭代步骤的数量。为了调整系数(a, b, c) ,我们有以下考虑:
- 我们希望a尽可能大,因为φ′(0) = a意味着该系数控制着较小初始奇异值的收敛速度。
- 对于每个x ∈ [0, 1],我们希望φN(x)收敛到范围[1 − ε, 1 + ε]内的某个值作为N → ∞,以便 NS 迭代的结果误差较小。
根据经验,ε可以高达 0.3 左右,而不会损害基于 Muon 的训练的损失曲线。因此,我们的目标是在 limN → ∞φN(x) ∈ [0.7, 1.3]的约束下最大化a。
解决这个约束优化问题有很多可能的方法。我们使用了一种基于梯度的临时方法,最终得到系数 (3.4445.4.7750.2.0315),这也是我们最终设计 Muon 时所用的系数。这些系数的变化如下图所示。请注意x = 0附近的增长更为陡峭。
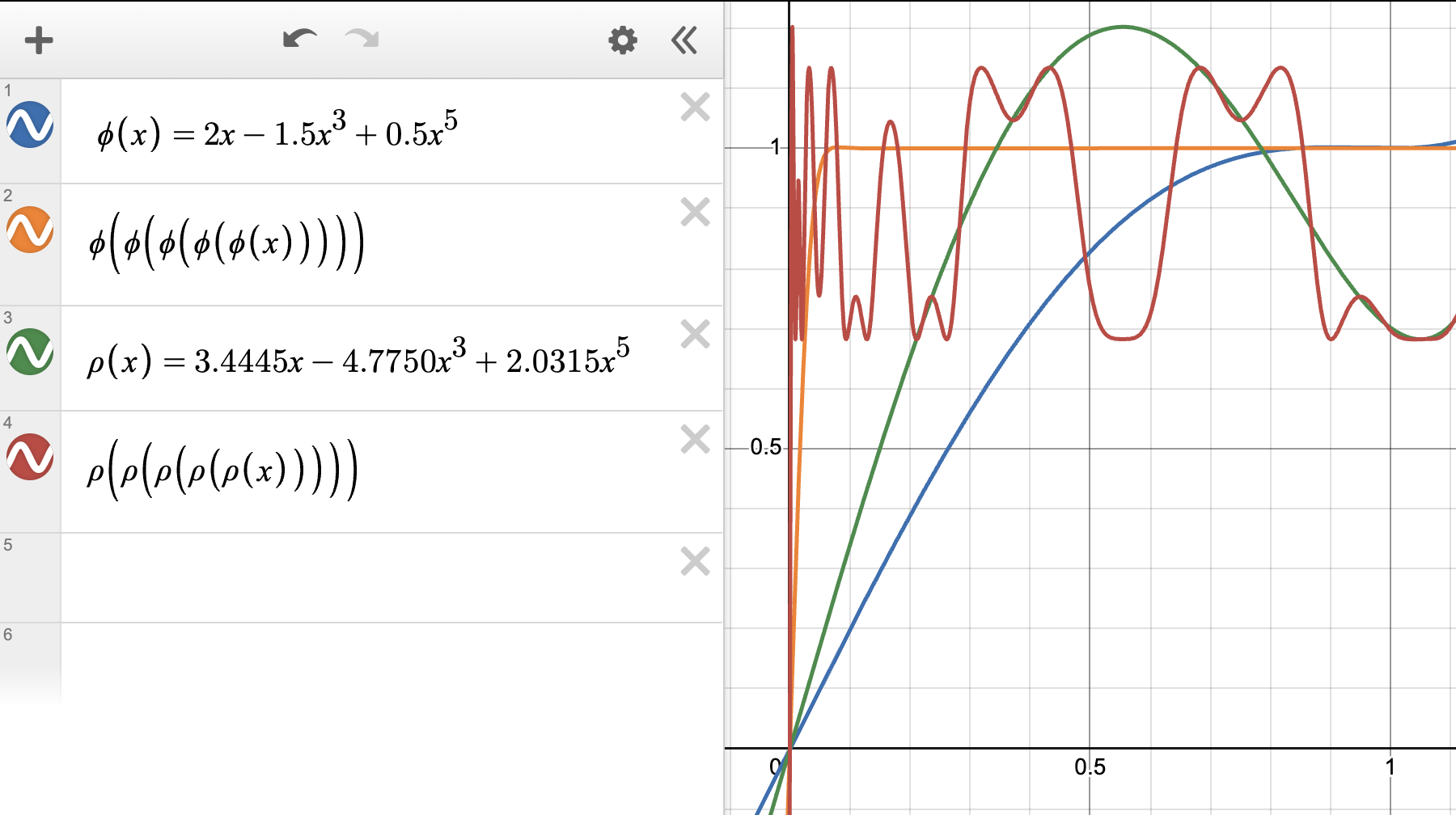
在我们的实验中,当使用具有这些系数的 Muon 来训练 Transformer 语言模型和小型卷积网络时,只需运行 5 步 NS 迭代就足够了。
2.2.2 牛顿–舒尔茨迭代介绍
这一步是 Muon 的核心创新,即对累积梯度Bt应用 Newton-Schulz 迭代以计算其近似正交化矩阵Ot。Newton-Schulz 迭代是一种用于近似计算矩阵函数(例如矩阵平方根或逆)的算法。这里它被用于逼近Bt的逆平方根(或相关变换),以达到正交化的效果。Muon使用固定步数的Newton-Schulz迭代来处理Bt,典型地迭代 5 次就能取得足够精度。在实现中,作者选择在半精度(bfloat16)下运行该迭代以提高效率,并发现这种迭代在低精度下仍然数值稳定。相比直接进行奇异值分解(SVD),Newton-Schulz迭代可以充分利用GPU的并行计算能力,大幅降低计算开销。例如,作者最初实现的Newton-Schulz迭代每次更新对形状为$nm的参数需约6nm2次浮点运算,随后经过改进将复杂度降低到4nm2 + 2m3(在实际中m ≤ n,因此复杂度进一步受限于参数矩阵较小的一维),显著提升了运算效率。通过这样处理,Muon在每步更新中增加的计算和内存开销相对可控,却换来了更有效的梯度方向调整。
2.2.3 Muon 原理分析
Muon 在每次迭代时首先使用常规方法计算梯度并累积动量,然后对动量梯度矩阵进行正交化(orthogonalization)处理,再用于更新权重。所谓对梯度矩阵正交化,是指找到一个与原梯度矩阵最接近的“半正交矩阵”作为更新,其中“半正交”意味着矩阵的行向量或列向量是正交的。等价地,这相当于将梯度矩阵进行奇异值分解,然后用 UV⊤替换原梯度——这一结果被称为“正交化梯度”。Muon 的更新步骤正是用这样的正交化梯度替代原始梯度动量进行参数调整。
那么,引入正交化的直观意义何在? 简单来说,它可以丰富更新的方向性。研究者通过对 Transformer 等网络的梯度观察发现,传统优化器产生的梯度更新矩阵往往条件数很高,接近于秩亏(也就是被少数几个主导方向所支配)。换言之,许多神经元对应的更新方向非常相似,梯度矩阵接近低秩。这意味着一些“罕见方向”(对应较小奇异值的方向)在更新中作用很弱,但这些方向可能对进一步降低损失仍然重要。通过正交化处理,Muon 实质上放大了这些罕见方向在更新中的作用,因为正交化将所有奇异值归一,无论原本大小,从而赋予每个独立方向以均等的尺度权重。这种调整有助于避免训练过程中某些重要方向被忽略,提高了搜索参数空间的效率。 从经验上看,正是这种对梯度更新方向分量的重新均衡,使得 Muon 相较于传统优化方法展现出更快的收敛和更高的效率。
在具体实现中,还有一些实用技巧和细节: - Muon 目前仅针对二维权重张量(包括将卷积核展平成矩阵的情况)应用。对于标量或向量参数(例如偏置项、LayerNorm 中的缩放参数等),以及输入层和输出层的权重,作者建议仍采用常规优化器 (如 AdamW) 进行训练。这部分原因在于:嵌入层(输入层)参数的优化动态确实有别于其他层,需要特殊对待;输出层是否需要区别对待则是基于经验的优化选择。实际实验表明,如果对 Transformer 模型的词嵌入层和最后分类头仍使用 AdamW 优化,而对中间的线性层使用 Muon 优化,能够取得最佳性能。 - 在动量的具体形式上,Muon 采用Nesterov动量略优于传统动量,因此作者在公开实现中将 Nesterov 作为默认方案。 - 对于 Transformer 中特有的多头注意力,研究者发现将查询 Q、键 K、值 V 各自的权重矩阵分别应用 Muon 优化效果更佳,而不是将它们合并为一个大矩阵一起正交化。这一拆分处理使每个子矩阵的正交化更精确,有助于训练稳定。上述这些实现层面的经验总结,体现了 Muon 在不同网络结构中的适配性和灵活性。
三、效果
将 CIFAR-10 上的训练速度记录提高到 94% 准确率,在A100上从3.3秒提高到2.6秒。
将 FineWeb(称为 NanoGPT 快速运行的竞赛任务)上的训练速度记录提高至 3.28 val loss,提高了 1.35 倍。
在扩展到 774M 和 1.5B 参数的同时,继续展示训练速度的提升。
在 HellaSwag 上训练了一个 1.5B 参数转换器,耗时 10 8xH100 小时,性能达到 GPT-2 XL 级别。使用 AdamW 达到相同结果则需要 13.3 小时。


下是 Muon 和 AdamW 在训练 15
亿参数语言模型时的对比。两个优化器均已调整。 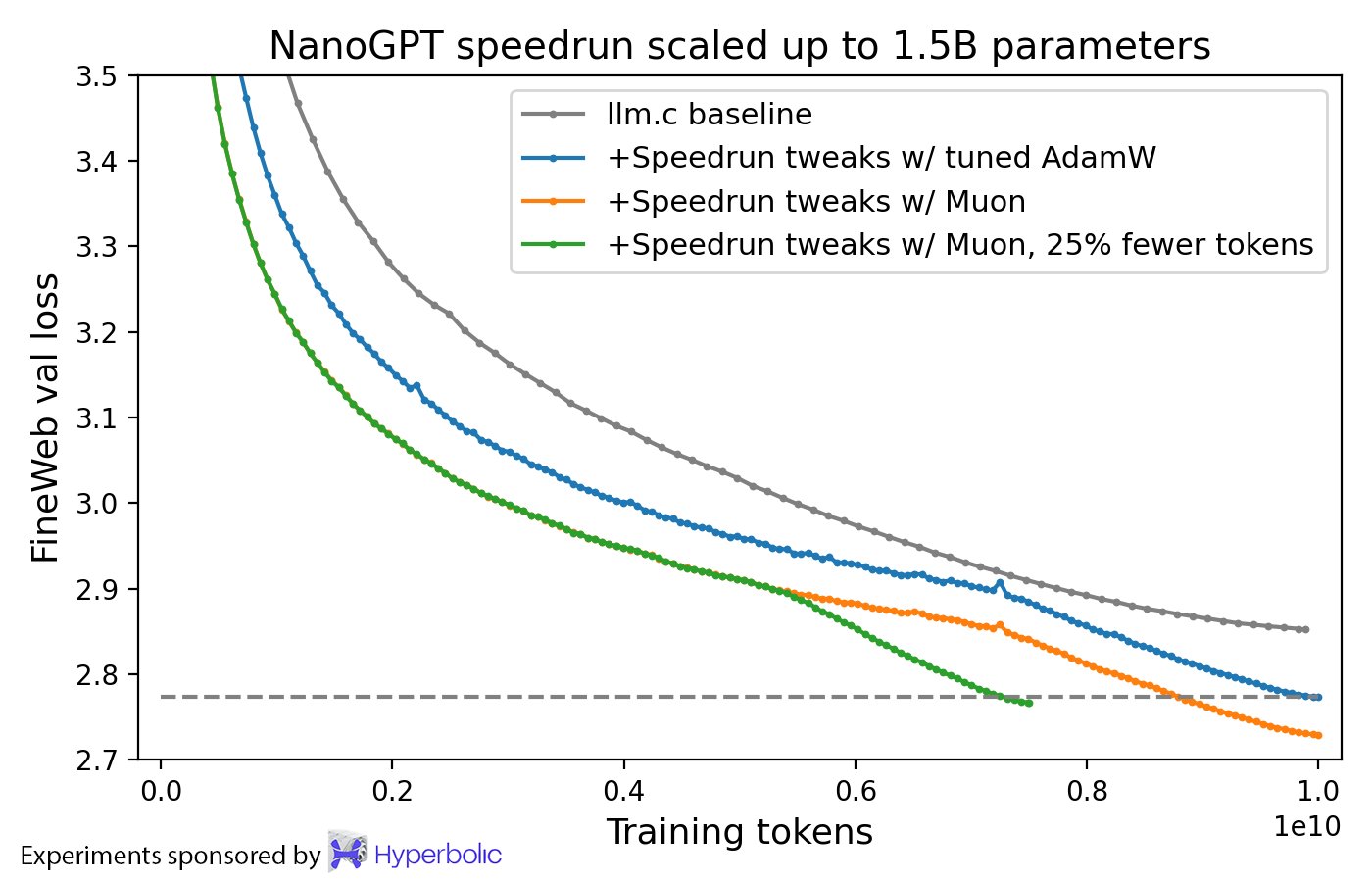
Reference
- Muon: An optimizer for hidden layers in neural networks
- Muon: An optimizer for hidden layers in neural networks(CSDN)
- Deriving Muon
- Muon优化器赏析:从向量到矩阵的本质跨越
- msign算子的Newton-Schulz迭代(上)
- msign算子的Newton-Schulz迭代(下)
- Why We Chose Muon: Our Chain of Thought
- Muon is Scalable for LLM Training
- Muon Code(Github)
- Old Optimizer, New Norm: An Anthology