重排:多样性算法

一、推荐系统中的多样性

如果多样性做得好，可以显著提升推荐系统的核心业务指标。

1.1 物品相似性的度量

• 基于物品属性标签。
  • 类⽬、品牌、关键词……
• 基于物品向量表征。
  • ⽤召回的双塔模型学到的物品向量（不好）。
  • 基于内容的向量表征（好）。

基于物品属性标签

• 物品属性标签：类⽬、品牌、关键词……
• 根据⼀级类⽬、⼆级类⽬、品牌计算相似度。
  • 物品i：美妆、彩妆、⾹奈⼉。
  • 物品j：美妆、⾹⽔、⾹奈⼉。
  • 相似度：sim₁(i, j) = 1, sim₂(i, j) = 0, sim₍i, j) = 1。

双塔模型的物品向量表征

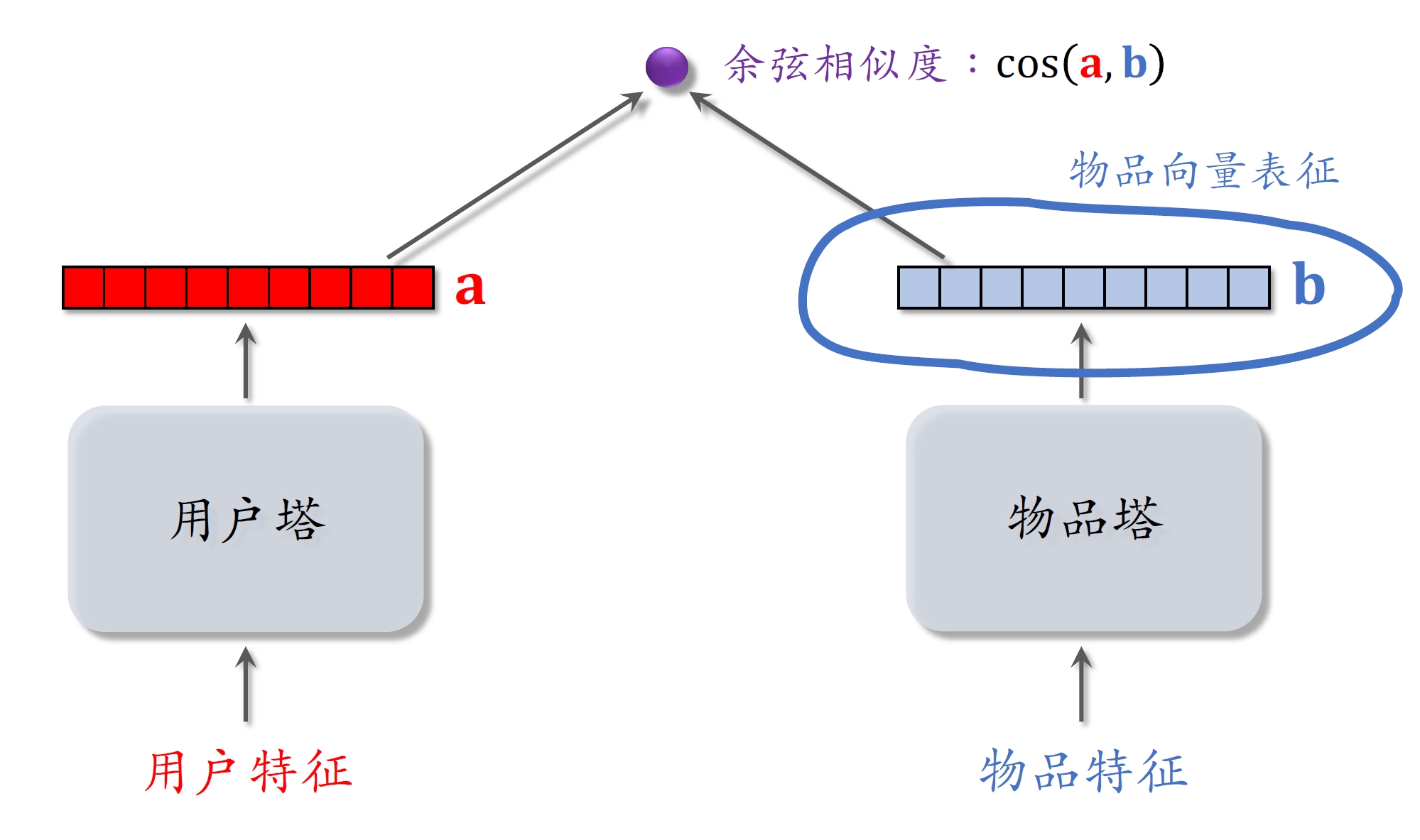
双塔模型的物品向量用在多样性问题上效果一般

• 因为推荐系统的头部现象很严重，曝光和点击都集中在少数物品
• 新物品和长尾物品的曝光和点击次数都很少，双塔模型学不好它们的向量表征

基于图文内容的物品表征

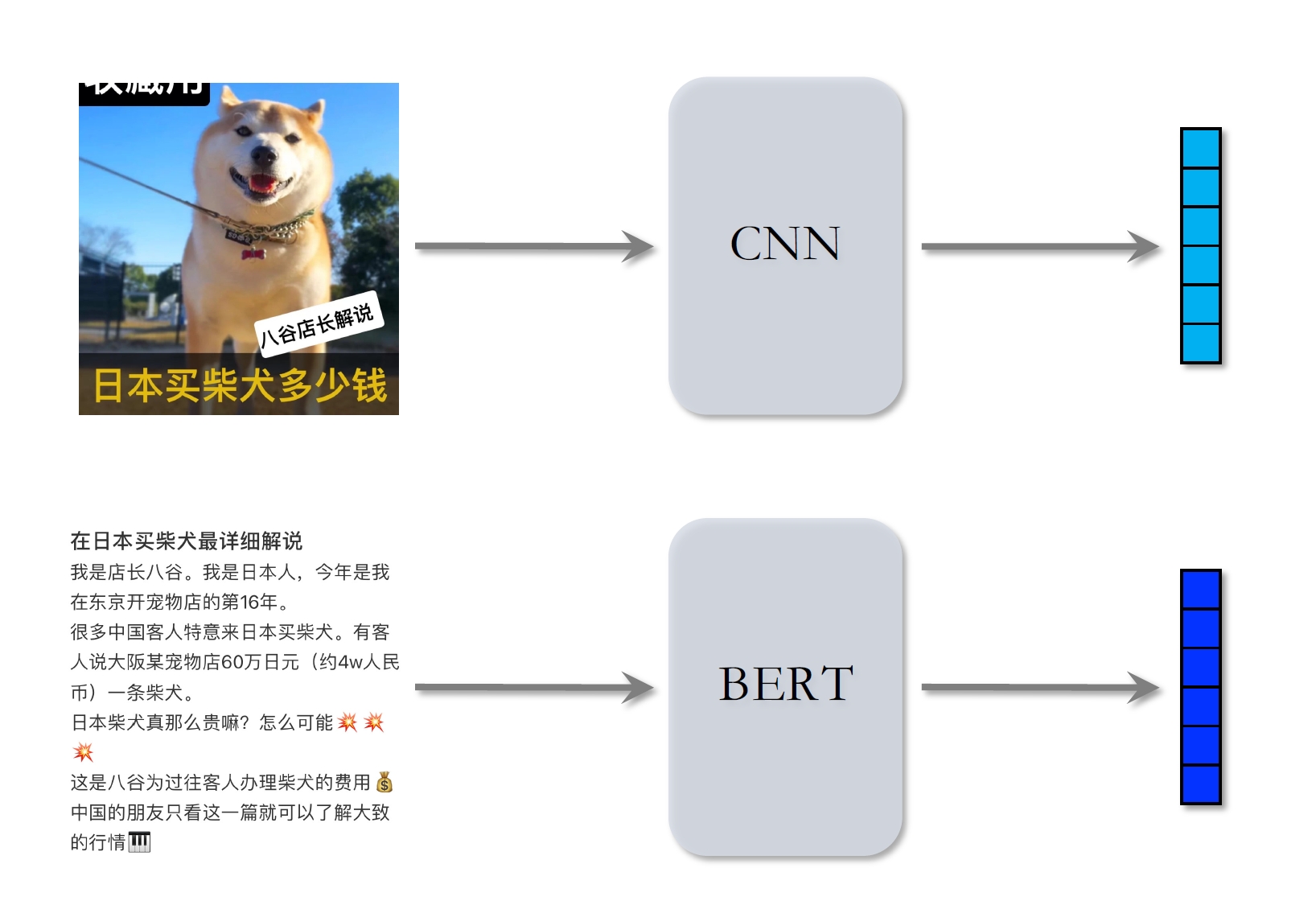
用在多样性问题上最好的办法还是基于图文内容的向量表征。

• CLIP^[1]是当前公认最有效的预训练⽅法。
• 思想：对于图⽚—⽂本⼆元组，预测图⽂是否匹配。

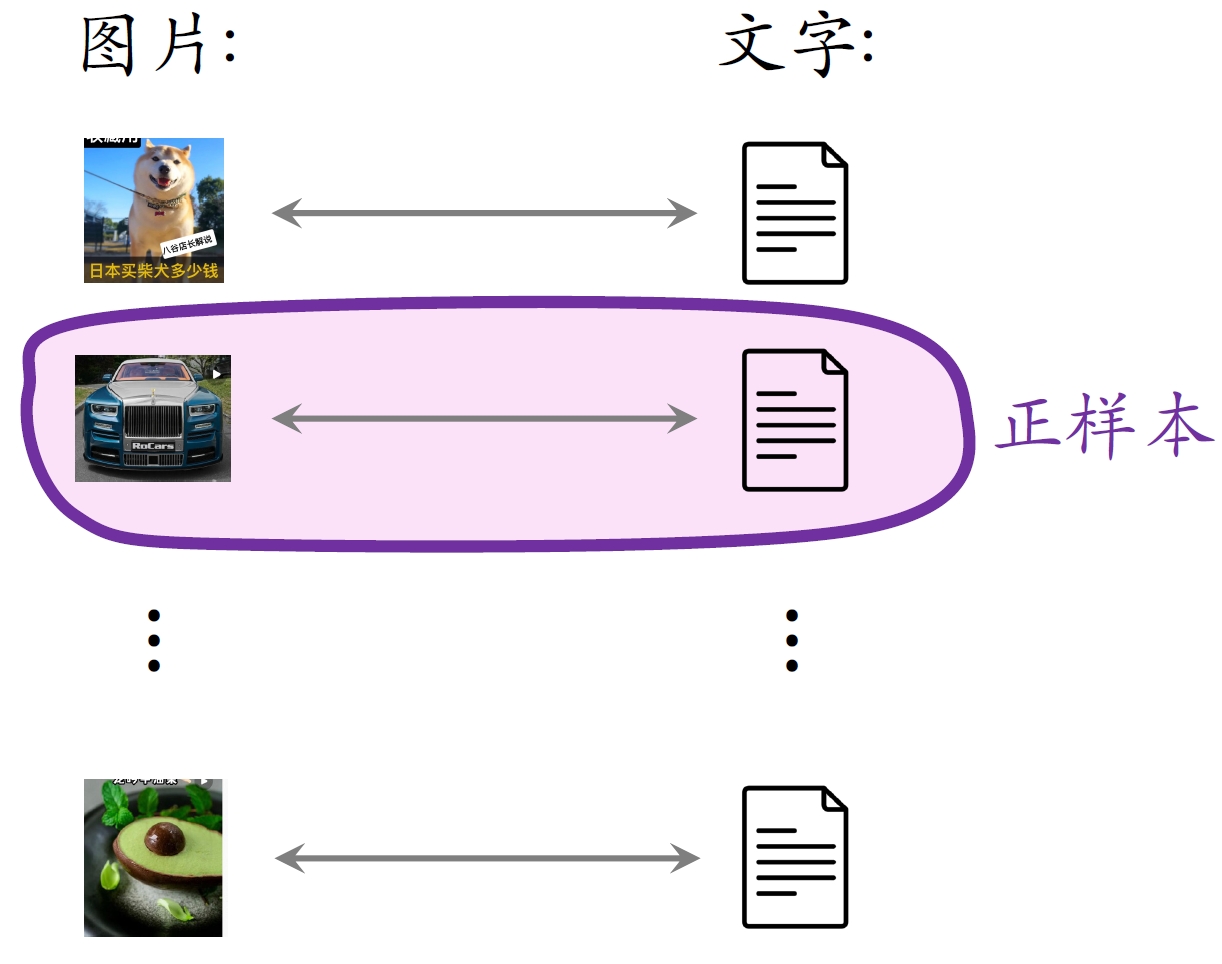
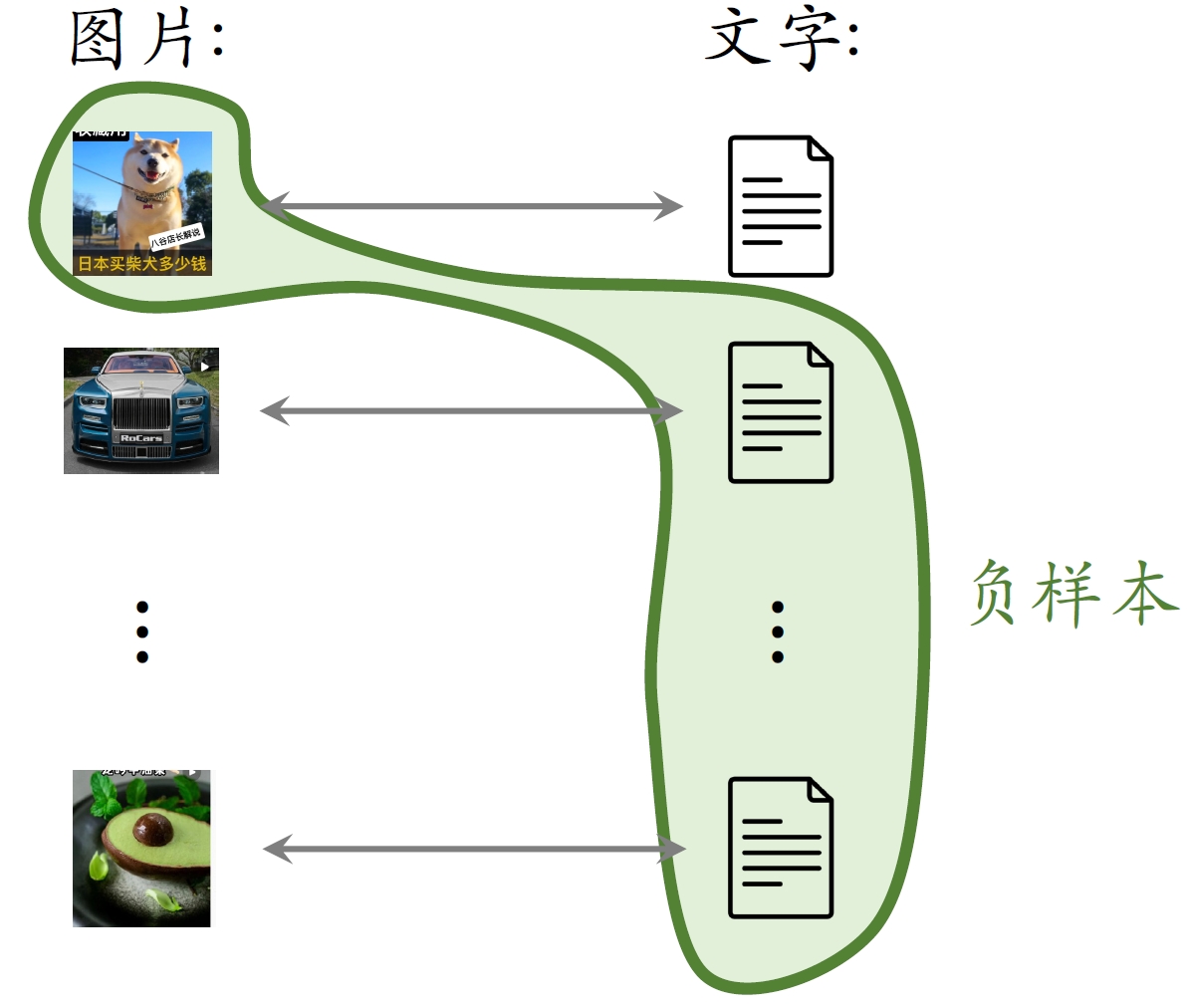
• ⼀个batch内有m对正样本。
• ⼀张图⽚和m − 1条⽂本组成负样本。
• 这个batch内⼀共有m(m − 1)对负样本。

1.2 提升多样性的⽅法

• 粗排和精排⽤多⽬标模型对物品做pointwise打分。
• 对于物品i，模型输出点击率、交互率的预估，融合成分数reward_i。
• reward_i 表⽰⽤户对物品i的兴趣，即物品本⾝价值。
• 给定n个候选物品，排序模型打分reward₁, ⋯, reward_n
• 从n个候选物品中选出k个，既要它们的总分⾼，也需要它们有多样性。

• 重排决定了n个候选物品中有哪k个最终获得曝光以及k个物品展示给用户的顺序
• 粗排的后处理往往被大家忽视
• 粗排之后的多样性算法也能提升业务指标:优化粗排之后的多样性显著提升了用户使用推荐的时长和留存

二、Maximal Marginal Relevance (MMR)

MMR根据精排打分和物品相似度，从 n 个物品中选出 k 个价值高、且多样性好的物品。MMR是从搜索排序中来的，所以名字里有relevance这个词(搜索的结果主要就是根据相关性做排序)。

多样性

• 精排给n个候选物品打分，融合之后的分数为reward₁, ⋯, reward_n
• 把第i和j个物品的相似度记作sim(i, j) 。
• 从n个物品中选出k个，既要有⾼精排分数，也要有多样性。

3.1 MMR多样性算法

计算集合ℛ中每个物品i的Marginal Relevance分数：

MR_i = θ ⋅ reward_i − (1 − θ) ⋅ max_{j ∈ 𝒮}sim(i, j)

• reward_i:物品i的精排分数
• max_{j ∈ 𝒮}sim(i, j): 物品i的多样性分数
• θ：0和1之间的参数，平衡物品的价值和多样性，θ越大则物品价值对排序的影响越大，多样性对物品排序的影响越小
• MMR:

MR平衡物品的价值和多样性:

• 既考虑物品本身的质量
• 也会抑制和已选中物品相似的物品

算法流程：

1. 已选中的物品𝒮初始化为空集，未选中的物品ℛ初始化为全集1, ⋯, n 。
2. 选择精排分数reward_i 最⾼的物品，从集合ℛ移到𝒮。
3. 做k − 1轮循环：
   1. 计算集合ℛ中所有物品的分数{MR_i}_{i ∈ ℛ}。
   2. 选出分数最⾼的物品，将其从ℛ移到𝒮。

3.2 滑动窗口

MMR:

上述方法缺点：

• 已选中的物品越多（即集合𝒮越⼤），越难找出物品i ∈ ℛ，使得i与𝒮中的物品都不相似。
• 设sim的取值范围是[0, 1]。当𝒮很⼤时，多样性分数max_{j ∈ 𝒮}sim(i, j)总是约等于1，导致MMR 算法失效。
• 解决⽅案：设置⼀个滑动窗⼝𝒲，⽐如最近选中的10个物品，⽤𝒲代替MMR 公式中的𝒮。

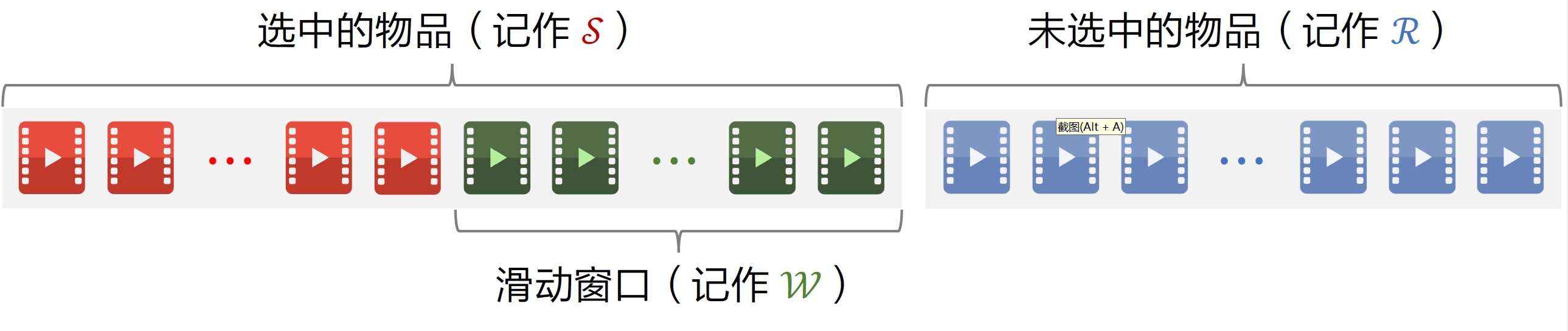
⽤滑动窗⼝的MMR:

• 只考虑未选中物品与滑动窗口中物品的相似性
• 工业界实际的重排都会使用滑动窗口滑动窗口
• 有个很直观的解释，给用户曝光的物品应当具有多样性，也就是说物品两两之间不相似，但没有必要让第三十个物品跟第一个物品不相似，用户看到第三十个物品的时候大概率已经忘记了第一个物品是什么，两个离得远的物品可以相似，相似也不会影响用户体验

三、业务规则

推荐系统有很多业务规则，比如不能连续出多篇某种类型的物品、某两种类型的物品文章间隔多少。这些业务规则应用在重排阶段，可以与 MMR、DPP 等多样性算法相结合。

规则：最多连续出现𝑘 篇某种文章

• 一般推荐系统的物品分为图⽂和视频。
• 假设最多连续出现k = 5篇图⽂，最多连续出现k = 5篇视频。
• 如果排i到i + 4的全都是图⽂，那么排在i + 5的必须是视频。

规则：每k篇文章最多出现1篇某种文章

• 运营推广文章的精排分会乘以⼤于1的系数（boost），帮助文章获得更多曝光。
• 为了防⽌boost 影响体验，限制每k = 9篇文章最多出现1篇运营推广文章。
• 如果排第i位的是运营推广文章，那么排i + 1到i + 8的不能是运营推广文章。

规则：前t篇文章最多出现k篇某种文章

• 排名前t篇文章最容易被看到，对⽤户体验最重要。（一般top 4为⾸屏）
• 推荐系统有带电商卡⽚的文章，过多可能会影响体验。
• 前t = 1篇文章最多出现k = 0篇带电商卡⽚的文章。
• 前t = 4篇文章最多出现k = 1篇带电商卡⽚的文章。

MMR + 重排规则

• 重排结合MMR 与规则，在满⾜规则的前提下最⼤化MR。
• 每⼀轮先⽤规则排除掉 ℛ中的部分物品，得到⼦集ℛ^′
• MMR 公式中的ℛ替换成⼦集ℛ^′，选中的物品符合规则。

引入规则，保护用户体验规则的优先级高于多样性算法。

四、determinantal point process (DPP)^[2]

行列式点过程 (determinantal point process, DPP) 是一种经典的机器学习方法，在 1970’s 年代提出，在 2000 年之后有快速的发展。DPP 是目前推荐系统重排多样性公认的最好方法。

4.1 数学基础

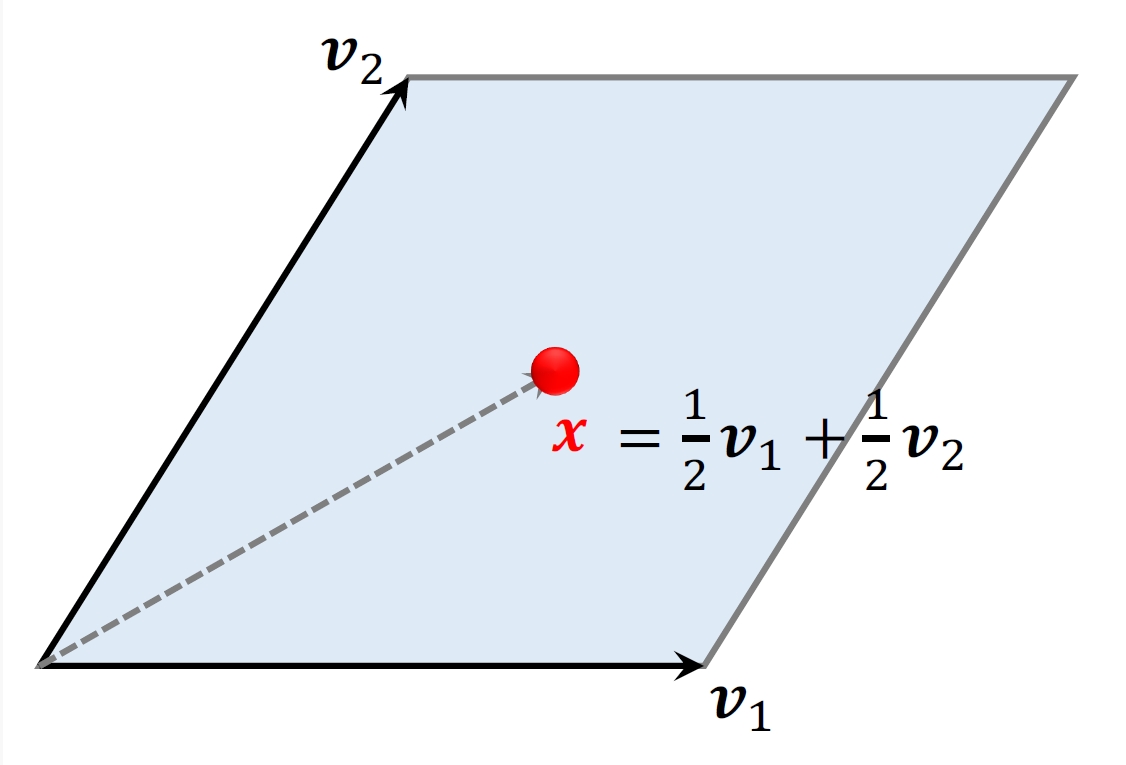
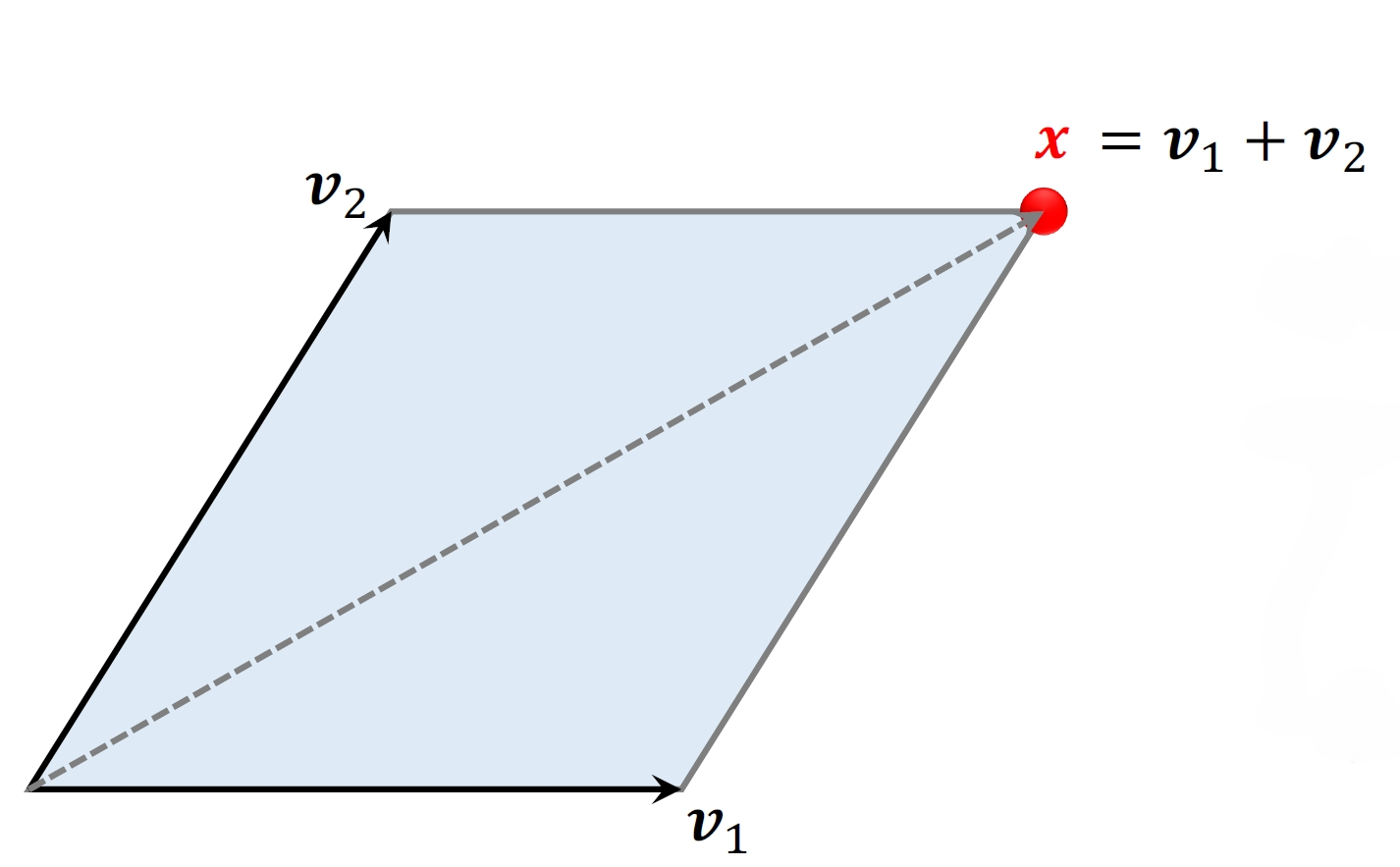
4.1.1 超平行体

• 2维空间的超平⾏体为平⾏四边形。
• 平⾏四边形中的点可以表⽰为：

x = α₁v₁ + α₂v₂

• 系数α₁, α₂取值范围是[0, 1]

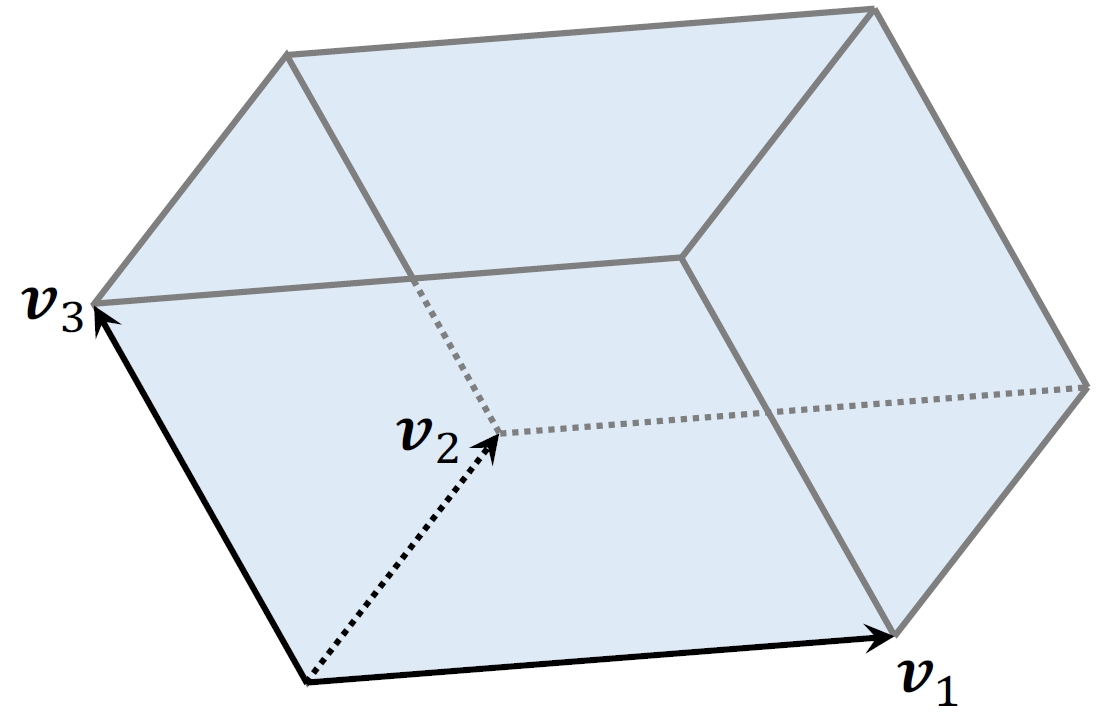
• 3维空间的超平⾏体为平⾏六⾯体。
• 平⾏六⾯体中的点可以表⽰为：

x = α₁v₁ + α₂v₂ + α₂v₃

• 系数α₁, α₂, α₃取值范围是[0, 1]

更高纬度：

• ⼀组向量v₁, ⋯, v_k ∈ ℝ^d可以确定⼀个k维超平⾏体：

𝒫(v₁, ⋯, v_k) = {α₁v₁ + ⋯ + α_kv_k|0 ≦ α₁, ⋯, α_k ≦ 1}

• 要求 k ≦ d,比如d = 3维空间中有k = 2维平⾏四边形。
• 如果v₁, ⋯, v_k线性相关，则体积vol(𝒫) = 0。（例：有k = 3个向量，落在⼀个平⾯上，则平⾏六⾯体的体积为0。）

4.1.2 平行四边形的面积

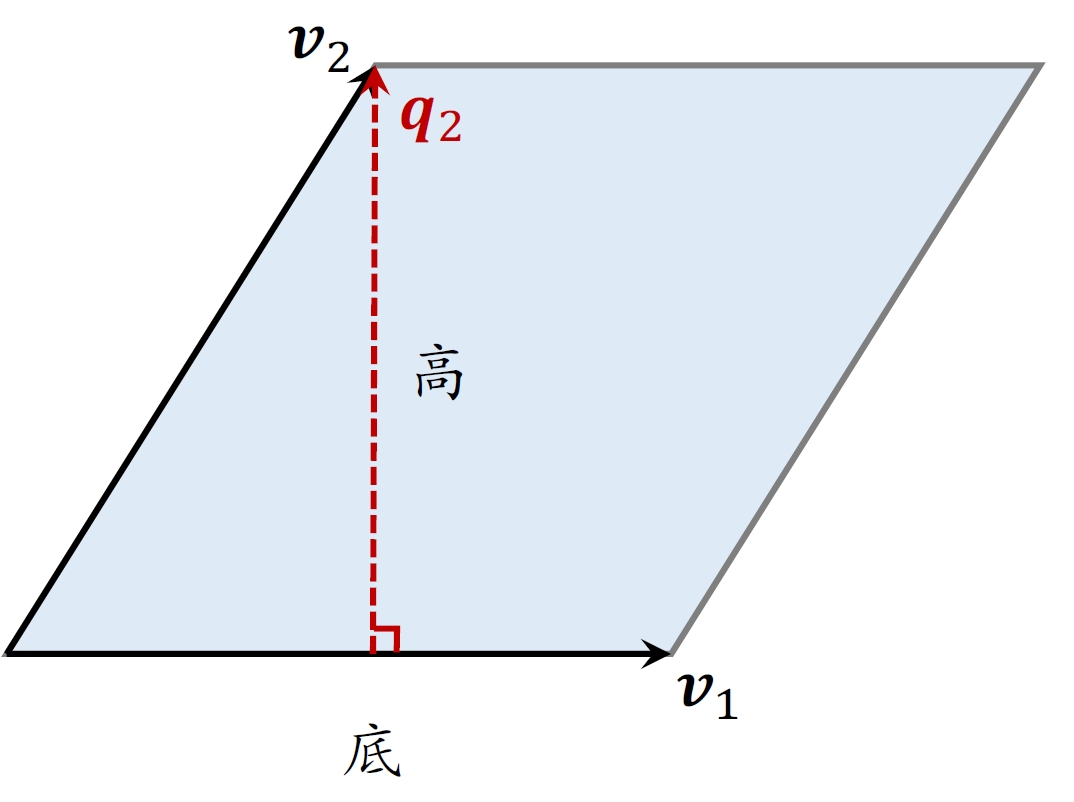
• ⾯积 = ∥底∥₂×∥高∥₂
• 以v₁为底，计算⾼q₂，两个向量必须正交。

以v₁为底，如何计算q₂

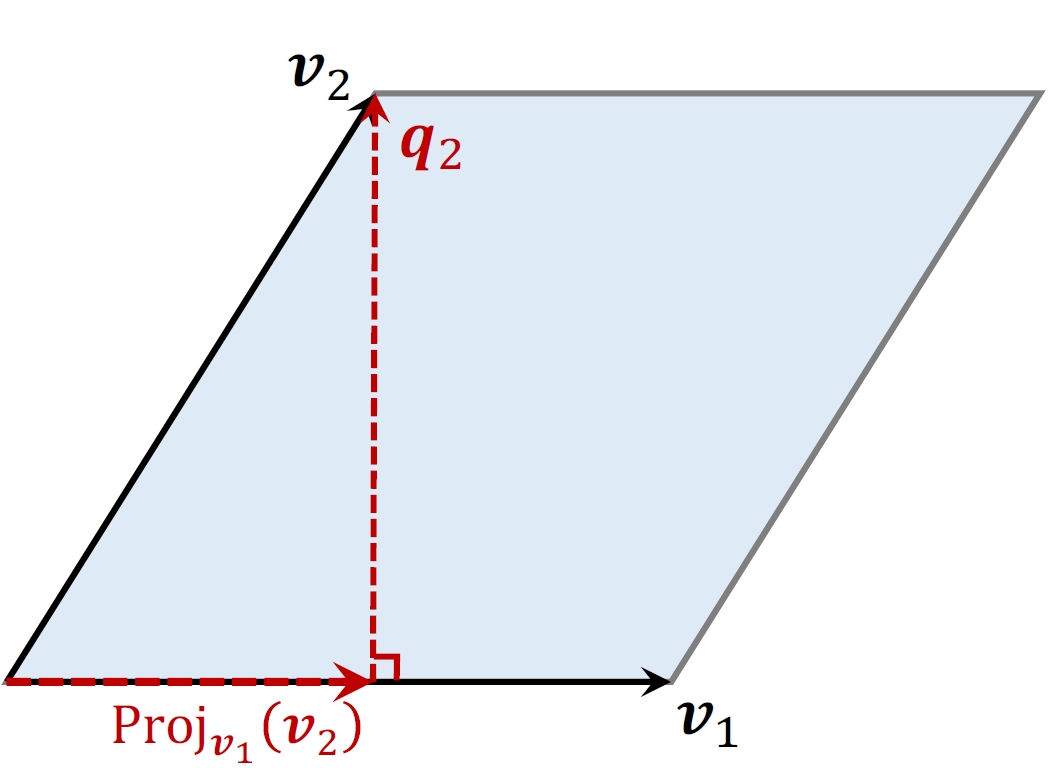
• 计算v₂在v₁上的投影：

• 计算q₂ = v₂−Proj_{v_1}(v_2)$
• 性质：底v₁与高q₂正交。

以v₂为底，如何计算q₁

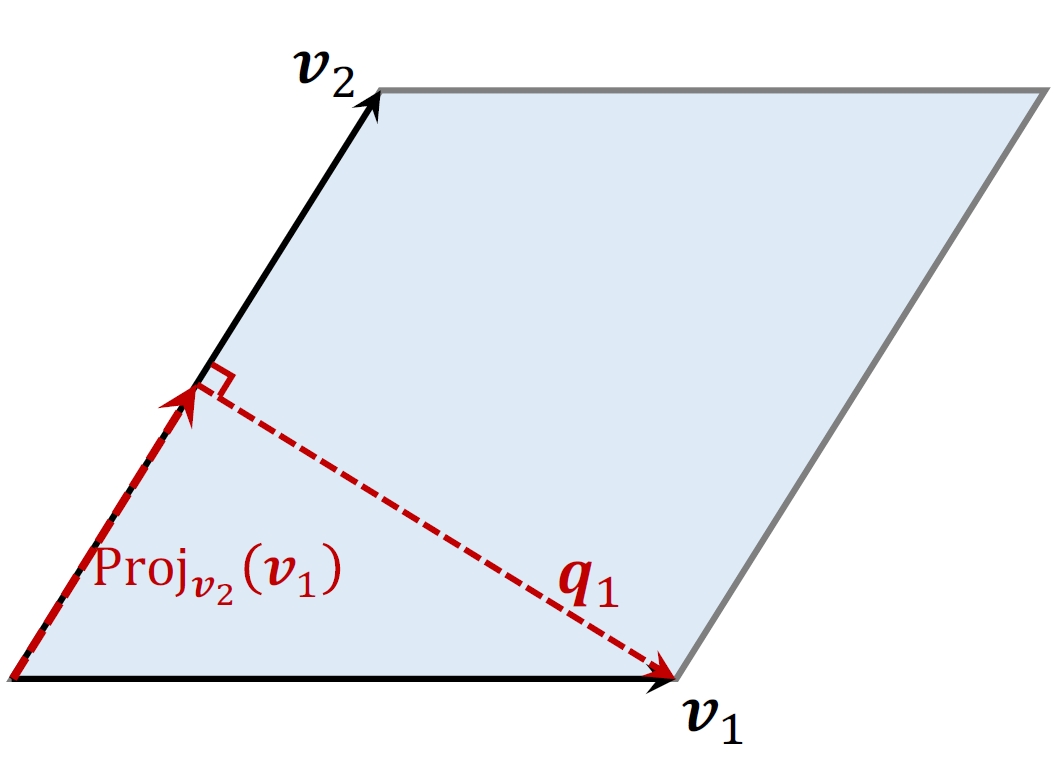
• 计算v₁在v₂上的投影：

• 计算q₁ = v₁ − Proj_v2(v₁)
• 性质：底v₂与高q₁正交。

4.1.3 平行六面体的体积

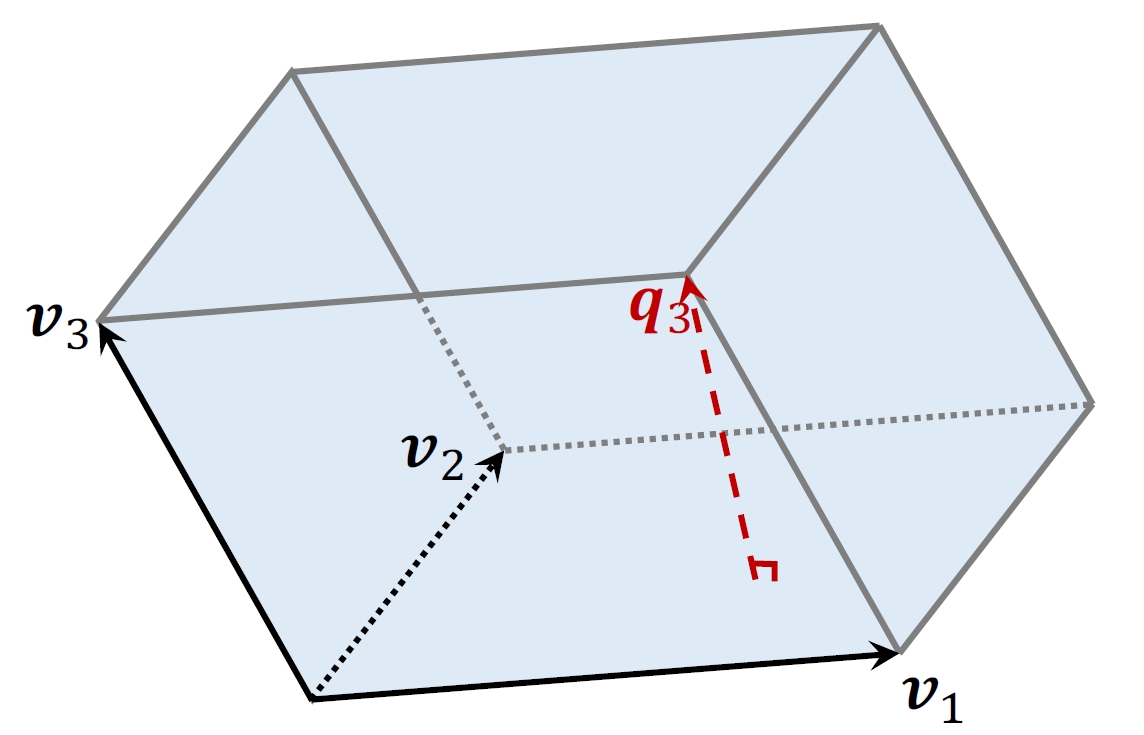
• 体积 = 底面积×∥高∥₂
• 平⾏四边形𝒫(v₁, v₂)是平⾏六⾯体𝒫(v₁, v₂, v₃)的底。
• 高q₃垂直于底𝒫(v₁, v₂).

体积何时最⼤化、最⼩化？

• 设 v₁, v₂, v₃都是单位向量。
• 当三个向量正交时，平⾏六⾯体为正⽅体，体积最⼤化，vol = 1
• 当三个向量线性相关时，体积最⼩化,vol = 0

衡量物品多样性

• 给定k个物品，把它们表征为单位向量v₁, ⋯, v_k ∈ ℝ^d。(k ≦ d)
• ⽤超平⾏体的体积衡量物品的多样性，体积介于0和1之间。
• 如果v₁, ⋯, v_k两两正交（多样性好），则体积最⼤化，vol = 1
• 如果v₁, ⋯, v_k线性相关（多样性差），则体积最⼩化，vol = 0

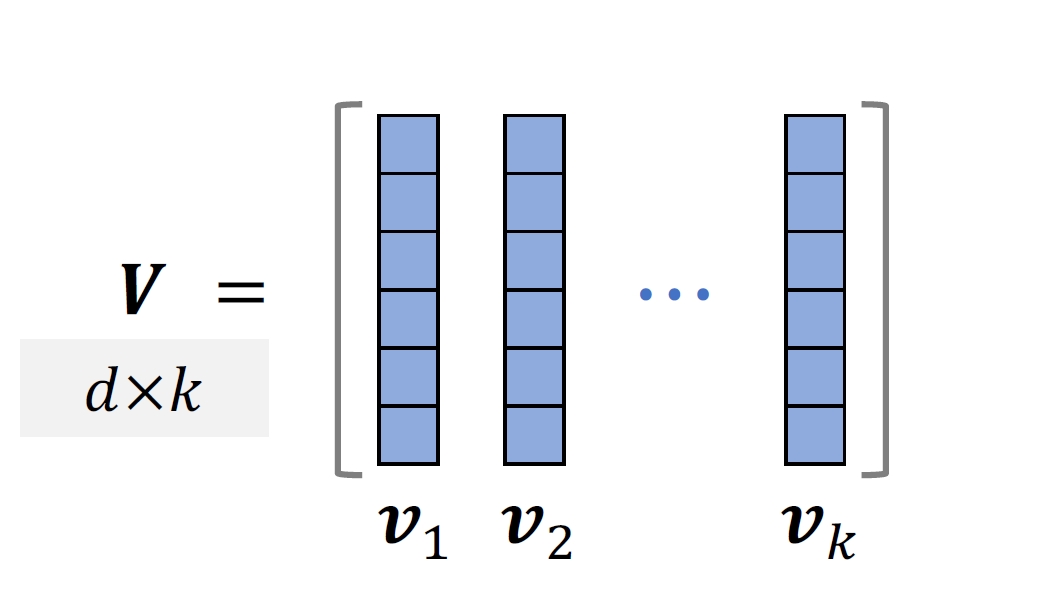
• 给定k个物品，把它们表征为单位向量v₁, ⋯, v_k ∈ ℝ^d。(k ≦ d)
• 把它们作为矩阵 V ∈ ℝ^d × k的列。
• 设 k ≦ d，⾏列式与体积满⾜：

det(V^TV) = vol(𝒫(v₁, ⋯, v_k))²

• 因此，可以⽤⾏列式det(V^TV)衡量向量v₁, ⋯, v_k的多样性。

4.2 DPP

4.2.1 多样性问题

• 精排给n个候选物品打分，融合之后的分数为reward₁, ⋯, reward_n
• n个物品的向量表征：v₁, ⋯, v_k ∈ ℝ^d
• 从n个物品中选出k个物品，组成集合𝒮
  • 价值⼤：分数之和∑_{j ∈ 𝒮}reward_j越⼤越好。
  • 多样性好：𝒮中k个向量组成的超平形体𝒫(𝒮)的体积越大越好。

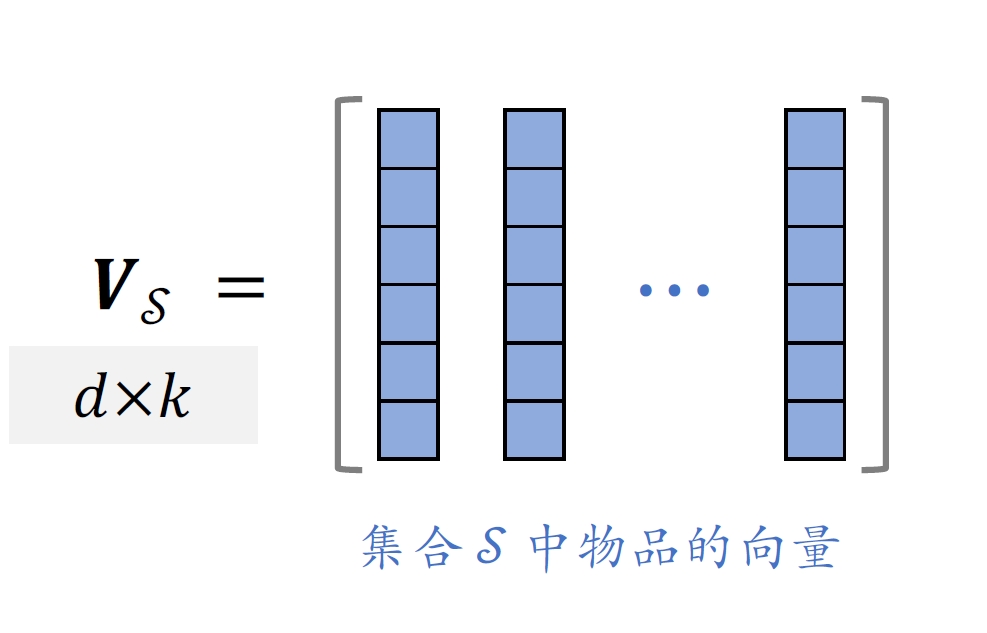
• 集合𝒮中的k个物品的向量作为列，组成矩阵V_𝒮 ∈ ℝ^d × k
• 以这k个物品的向量作为边，组成超平形体𝒫(𝒮)
• 体积vol(𝒫(𝒮))可以衡量𝒮中物品的多样性
• 设 k ≦ d，⾏列式与体积满⾜：

det(V_𝒮^TV_𝒮) = vol(𝒫(𝒮))²

4.2.2 DPP

DPP是目前推荐系统领域公认最好的多样性算法，工业界的推荐系统大多使用类似的方法。DPP多样性算法:最大化超平行体体积(最理想情况:t物品向量两两正交，则两两之间的相似度最小)。

• DPP是⼀种传统的统计机器学习⽅法：

• Hulu的论⽂^[3]将DPP应⽤在推荐系统：

DPP应⽤在推荐系统

• 设A为n × n的矩阵，它的(i, j)元素为a_ij = v_i^Tv_j
• 给定向量v₁, ⋯, v_n ∈ ℝ^d，需要O(n²d)时间计算A
• A_𝒮 = V_𝒮^TV_𝒮为A的一个k × k的子矩阵。如果i, j ∈ 𝒮，则a_ij是A_𝒮的一个元素

• DPP是个组合优化问题，从集合{1, ⋯, n}中选出⼀个⼤⼩为k的子集𝒮
• 用𝒮表⽰已选中的物品，⽤ℛ表⽰未选中的物品，贪⼼算法求解：

用DPP每次选出未选中物品中分数最大的

4.3 求解DPP

4.3.1 暴力算法

• 贪⼼算法求解：

• 对于单个i，计算A_{𝒮 ∪ {i}}的⾏列式需要O(|𝒮|³)时间
• 对于所有的i ∈ ℛ，计算⾏列式需要时间O(|𝒮|³ ⋅ |ℛ|)
• 需要求解上式k次才能选出k个物品。如果暴⼒计算⾏列式，那么总时间复杂度为

O(|𝒮|³ ⋅ |ℛ|⋅k) = O(nk⁴)

• 暴⼒算法的总时间复杂度为

O(n²d + nk⁴)

n²d:计算矩阵A的时间 nk⁴:计算行列式的时间n的量级是几百，k和d的量级都是几十这个时间复杂度看起来OK，但其实不可行，因为系统留给多样性算法的时间也就是10毫秒左右，这个算法太慢了

4.3.2 Hulu的快速算法

Hulu的论⽂设计了⼀种数值算法，仅需O(n²d + nk²)的时间从n个物品中选出k个物品。

• 给定向量v₁, ⋯, v_n ∈ ℝ^d，需要O(n²d)时间计算A
• 用O(nk²)时间计算所有的⾏列式（利⽤Cholesky 分解）。

Cholesky 分解

• Cholesky 分解A_𝒮 = LL^T，其中L是下三⾓矩阵（对⾓线以上的元素全零）。
• Cholesky 分解可供计算A_𝒮的⾏列式。
  • 下三⾓矩阵L的⾏列式det(L)等于L对⾓线元素乘积。
  • A_𝒮的⾏列式det(A_𝒮) = det(L)² = ∏_il_ii²
• 已知A_𝒮 = LL^T，则可以快速求出所有A_{𝒮 ∪ {i}}的Cholesky分解，因此可以快速算出所有A_{𝒮 ∪ {i}}的⾏列式。

贪⼼算法求解：

• 初始时𝒮中只有⼀个物品，A_𝒮是1 × 1的矩阵

• 每⼀轮循环，基于上⼀轮算出的A_𝒮 = LL^T，快速求出A_{𝒮 ∪ {i}}的Cholesky 分解（∀i ∈ ℛ），从⽽求出log det(A_{𝒮 ∪ {i}})

• 已知矩阵A_𝒮的Cholesky分解，那么给A_𝒮添加一行和一列不需要重新算一遍Cholesky分解，否则代价很大。

• 给A_𝒮添加一行和一列，Cholesky分解的变化非常小，有办法快速算出变化的地方，这样就不用完整算-遍Cholesky分解

4.4 DPP的扩展

4.4.1 滑动窗口

• 用𝒮表⽰已选中的物品，⽤ℛ表⽰未选中的物品，DPP的贪⼼算法求解：

• 随着集合𝒮增⼤，其中相似物品越来越多，物品向量会趋近线性相关。
• ⾏列式 det(A_𝒮)会坍缩到零，对数趋于负无穷。

⽤滑动窗⼝的:

4.4.2 规则约束

• 贪⼼算法每轮从ℛ中选出⼀个物品：

• 有很多规则约束，例如最多连续出5篇视频（如果已经连续出了5篇视频，下⼀篇必须是图⽂）。

• ⽤规则排除掉ℛ中中的部分物品，得到⼦集ℛ^′，然后求解：

1. https://arxiv.org/abs/2103.00020 ↩︎
2. https://arxiv.org/abs/1709.05135 ↩︎
3. https://arxiv.org/abs/1709.05135 ↩︎