隐马尔科夫模型

隐马尔科夫模型(Hidden Markov Model, HMM)是可用于标注问题的统计学习模型，描述由隐藏的马尔科夫链随机生成观测序列的过程，属于生成模型。

1. HMM 的基本概念

1.1 HMM 的定义

HMM 是关于时序的概率模型，描述一个隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔科夫链随机生成的状态的序列，称为状态序列(State Sequence);每一个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列(Observation Seqyence).序列的每一个位置又可以看作一个时刻。

HMM 由初始概率分布、状态转移概率分布以及观测概率分布确定。HMM的形式如下:

设 Q 是所有可能的状态集合， V 是所有可能的观测的集合。

Q = {q₁, q₂, ⋯, q_N},   V = {v₁, v₂, ⋯, v_M}

其中， N 是可能的状态数， M 是可能的观测数。

I 是长度为 T 的状态序列， O 是对应的观测序列:

I = (i₁, i₂, ⋯, i_T),   O(o₁, o₂, ⋯, o_T)

A 是状态转移矩阵:

A = [a_ij]_N × N

其中，

a_ij = P(i_t + 1 = q_j|i_t = q_i),   i = 1, 2, ⋯, N;  j = 1, 2, ⋯, N

是在时刻 t 处于状态 q_i 的条件下在时刻 t + 1 转移到状态 q_j 的概率。

B 是观测概率矩阵:

B = [b_j(k)]_N × M

其中，

b_j(k) = P(o_t = v_k|i_t = q_j),   i = 1, 2, ⋯, M;  j = 1, 2, ⋯, N

是在时刻 t 处于状态 q_j 的条件下生成观测 v_k 的概率。

π 是初始状态概率向量:

π = (π_i)

其中，

π_i = P(i₁ = q_i),    i = 1, 2, ⋯, N

是时刻 t = 1 处状态 q_i 的概率。

HMM 由初始状态概率向量 π 、状态转移概率矩阵 A 和观测概率矩阵 B 决定。 π 和 A 决定状态序列， B 决定观测序列。因此， HMM  λ 可以用三元符号表示，即

λ = (A, B, π)

A, B, π 称为 HMM 的三要素。

状态转移矩阵 A 与初始状态概率向量 π 确定了隐马尔科夫链，生成不可观测的状态序列。观测概率矩阵 B 确定了如何从状态生成观测，与状态序列综合取得了如何产生观测序列。

HMM 作了两个基本假设:

1. 齐次马尔科夫性假设，即假设隐藏的马尔科夫链在任意时刻 t 的状态值依赖于前一时刻的状态，与其他时刻的状态及观测无关，也与时刻 t 无关。

P(i_t|i_t − 1, o_t − 1, ⋯, i₁, o₁) = P(i_t|i_t − 1),   t = 1, 2, ⋯, T

2. 观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态，与其他观测及状态无关。

P(o_t|i_T, o_T, i_T − 1, o_T − 1, ⋯, i_t + 1, o_t + 1, i_t, i_t − 1, o_t − 1, ⋯, i₁, o₁) = P(o_t|i_t)

HMM 可用于标注，这时状态对应着标记。标注问题是给定观测的序列预测去对应的标记序列。可以假设标注问题的数据是由 HMM 生成的。这样就可以利用 HMM 的学习与预测算法进行标注。

例(盒子和球模型)

假设有4个盒子，每个盒子里都装有红白两种颜色的球，盒子里的红白球数如下表:

盒子	1号	2号	3号	4号
红球数	5	3	6	8
白球数	5	7	4	2

抽球方法:开始，以等概率随机从4个盒子里选取1个盒子，从盒子里随机抽出1个球，记录颜色后放回；然后从当前盒子转移到下一个盒子，规则:如果当前盒子是1号，那么 下一个盒子一定是2号，如果当前盒子是2号或3号，那么分别以概率0.4和0.6转移到左边或右边的盒子，如果当前盒子是4号，那么各以0.5的概率停留在盒子4或转移到盒子3；确定转移的盒子后，再从这个盒子里随机抽出1个求，记录其颜色并放回；如此下去重复5次，得到 一个球的颜色的观测序列:

O = {Red, Red, White, White, Red}

在这个过程中，只能观测到求颜色的序列，不能观测到球是从哪个盒子取出的，即观测不到盒子的序列。

这个例子中有两个随机序列，一个是盒子的序列(状态序列)，一个是球颜色的观测序列(观测序列)。前者是隐藏的，只有后者是可观测的。这是 HMM 的例子:

盒子对应状态，状态的集合:

Q = {Box1, Box2, Box3, Box4},      N = 4

球的颜色对应观测。观测序列集合:

V = {Red, White},     M = 2

状态序列和观测序列长度 T = 5 .

初始概率分布:

π = (0.25, 0.25, 0.25, 0.25)^T

状态转移概率分布

观测概率分布

1.2 观测序列的生成过程

根据 HMM 的定义，可以将一个长度为 T 的观测序列 O = (o₁, o₂, ⋯, o_T) 的生成过程描述如下:

输入: HMM   λ = (A, B, π) ，观测序列长度 T ;

输出：观测序列 O = (o₁, o₂, ⋯, o_T) 。

1. 按照初始状态分布 π 产生状态 i₁

2. 令 t = 1

3. 按照状态 i_t 的观测概率分布 b_it(k) 生成 o_t

4. 按照状态 i_t 的状态转移概率分布

{a_itit + 1}

        产生状态 i_t + 1,  i_t + 1 = 1, 2, ⋯, N

5. 令 t = t + 1 ；如果 t < T ，转(3);否则，终止

1.3 HMM 的三个基本问题

(1)概率计算问题，给定模型 λ = (A, B, π) 和观测序列 O = (o₁, o₂, ⋯, o_T) ，计算在模型 λ 下观测序列 O 出现的概率 P(O|λ)

(2)学习问题。已知观测序列 O = (o₁, o₂, ⋯, o_T) ，估计模型 λ = (A, B, π) 参数，使得在该模型下观测序列概率 P(O|λ) 最大.即用极大似然估计参数。

(3)预测问题，也称为解码(decoding)问题。已知模型 λ = (A, B, π) 和观测序列 O = (o₁, o₂, ⋯, o_T) ，求给定观测序列条件概率 P(I|O) 最大的状态序列 O = (i₁, i₂, ⋯, i_T) .即给定观测序列，求最有可能的对应的状态序列。

2. 概率计算算法

2.1 直接计算

给定模型 λ = (A, B, π) 和观测序列 O = (o₁, o₂, ⋯, o_T) ，计算观测序列 O 出现的概率 P(O|λ) .最直接的方法是按概率公式直接计算。通过列举所有可能的长度为 T 的状态序列 I = (i₁, i₂, ⋯, i_T) ，求各个状态序列 I 与观测序列 O = (o₁, o₂, ⋯, o_T) 的联合概率 P(O, I|λ) ,然后对所有可能的状态序列求和，得到 P(O|λ) 。

状态序列 I = (i₁, i₂, ⋯, i_T) 的概率是

P(I|λ) = π_i1a_i1i2a_i2i3⋯a_{iT − 1iT}

对固定状态序列 I = (i₁, i₂, ⋯, i_T) ，观测序列 O = (o₁, o₂, ⋯, o_T) 的概率是

P(O|I, λ) = b_i1(o₁)b_i2(o₂)⋯b_iT(o_T)

O 和 I 同时出现的联合概率为

然后对所有可能的状态序列 I 求和，得到观测序列 O 的概率：

P(O|λ) = ∑_IP(O|I, λ)P(I|λ) = ∑_{i1, i2, ⋯, iT}π_i1b_i1(o₁)a_i1i2b_i2(o₂)a_i2i3⋯a_{iT − 1iT}b_iT(o_T)

上式的计算量是 O(TN^T) 阶的，计算量过大，此方法不可行。

2.2 前向算法

前向概率: 给定 HMM   λ ，定义到时刻 t 部分观测序列为 o₁, o₂, ⋯, o_t 且状态为 q_i 的概率为前向概率，记作

α_t(i) = P(o₁, o₂, ⋯, o_t, i_t = q_i|λ)

可以递推地求前向概率 α_t(i) 及观测序列概率 P(O|λ) .

观测序列概率的前向算法

输入: HMM  λ ,观测序列 O ；

输出: 观测序列概率 P(O|λ) .

(1)初值

α₁(i) = π_ib_i(o₁),   i = 1, 2, ⋯, N

(2)递推 对 t = 1, 2, ⋯, T − 1

(3)终止

(1)初始化前向概率，是初始时刻的状态 i₁ = q_i 和观测 o₁ 的联合概率。(2)是前向概率的递推公式，计算到时刻 t + 1 部分观测序列为 o₁, o₂, ⋯, o_t, o_t + 1 且在时刻 t + 1 处于状态 q_i 的前向概率，如图。

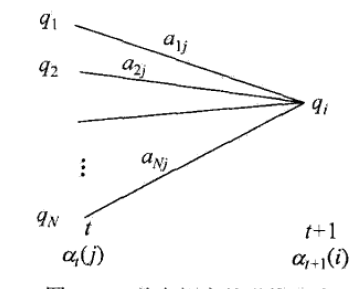
在递推公式的方括号里, α_t(j) 是时刻 t 观测到 o₁, o₂, ⋯, o_t 并在时刻 t 处于状态 q_j 的前向概率，那么乘积 α_t(j)a_ji 就是是时刻 t 观测到 o₁, o₂, ⋯, o_t 并在时刻 t 处于状态 q_j 而在时刻 t + 1 到达状态 q_i 的联合概率。对于这个乘积在时刻 t 的所有可能的 N 个状态 q_j 求和，其结果解释到时刻 t 观测为 o₁, o₂, ⋯, o_t 并在时刻 t + 1 处于状态 q_i 的联合概率。方括号里的值与观测概率 b_i(o_t + 1) 的乘积恰好就是是到时刻 t + 1 观测到 o₁, o₂, ⋯, o_t, o_t + 1 并在时刻 t + 1 处于状态 q_i 的前向概率 α_t + 1(i).

(3)因为

α_T(i) = P(o₁, o₂, ⋯, o_t, i_T = q_i|λ)

所以

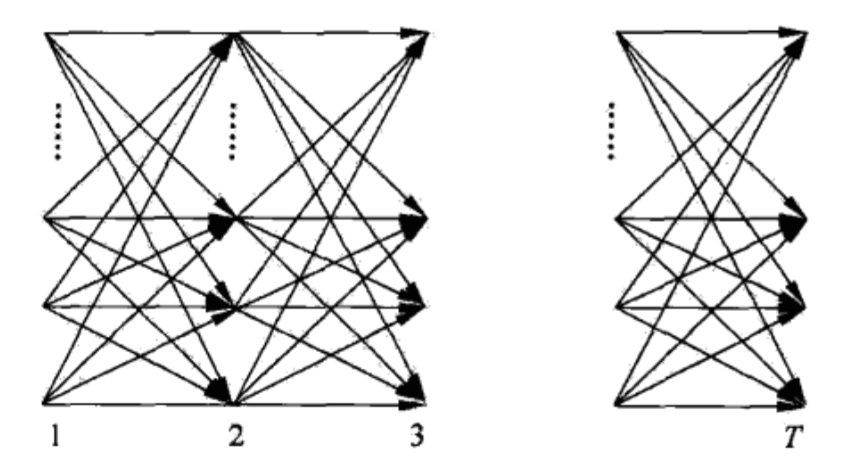
如上图，前向算法实际是基于状态序列的路径结构递推计算 P(O|λ) 的算法。前向算法高效的关键是其具备计算前向概率，然后利用路径结构将前向概率递推到全局，得到 P(O|λ) .具体地，在时刻 t = 1 ，计算 α₁(i) 的 N 个值 (i = 1, 2, ⋯, N) ；在各个时刻 i = 1, 2, ⋯, T − 1 ，计算 α_t + 1(i) 的 N 个值, 而且每个 α_t + 1(i) 的计算利用前一时刻 N 个 α_t(j) .减少计算量的原因在于每一次计算直接引用前一时刻的计算结果，避免重复计算。这样利用前向概率计算 P(O|λ) 的计算量是 O(N²T) 阶的。

例

考虑盒子和球模型 λ = (A, B, π) ，状态集合

Q = {1, 2, 3}

观测集合

V = {Red, White}

设 T = 3, O = (Red, White, Red) ,用前向算法计算 P(O|λ)

解

(1)计算初值

(2)递推计算

(3)终止

2.3 后向算法

后向概率: 给定 HMM   λ ，定义在时刻 t 状态为 q_i 的条件下，从 t + 1 到 T 的部分观测序列为 o_t + 1, o_t + 2, ⋯, o_T 的概率为后向概率，记作

β_t(i) = P(o_t + 1, o_t + 2, ⋯, o_T|i_t = q_i, λ)

可以用递推地方法求得后向概率 β_t(i) 及观测序列概率 P(O|λ) 。

观测序列概率的后向算法

输入: HMM  λ ,观测序列 O ；

输出: 观测序列概率 P(O|λ) .

(1)初值

β_T(i) = 1,   i = 1, 2, ⋯, N

(2)递推 对 t = T − 1, T − 2, ⋯, 1

(3)终止

(1)初始化后向概率，对最终时刻的所有状态 q_i 规定 β_T(i) = 1 。(2)是后向概率的递推公式。

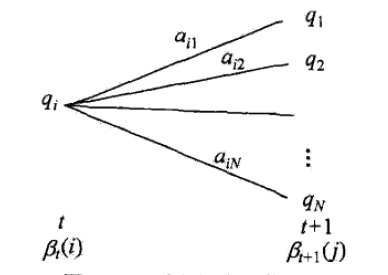
如上图，为了计算在时刻 t 状态为 q_i 条件下时刻 t + 1 之后的观测序列为 o_t + 1, o_t + 2, ⋯, o_T 的后向概率 β_t(i) ，只需考虑在时刻 t + 1 所有可能的 N 个状态 q_j 的转移概率 ( a_ij 项)，以及在此状态下的观测 o_t + 1 的观测概率( b_j(o_t + 1) 项)，然后考虑状态 q_j 之后的观测序列的后向概率( β_t + 1(j) 项)。(3)求 P(O|λ) 的思路与步骤(2) 一致，只是初始概率 π_i 代替转移概率。

利用前向概率和后向概率的定义可以将观测序列概率 P(O|λ) 统一写成

此式当 t = 1 和 t = T − 1 时分别代表前向概率和后向概率所求的观测序列概率。从 t = 1 时刻不断向前递推，将得到前向算法的计算公式，从 t = T − 1 时刻不断向后递推，将得到后向算法的计算公式。

把 t = T − 1 代入，得

由于 α 是对 i 的累加，与 j 无关，于是上式可变化为：

由 β_t(i) 的递推公式:

得

由 α_T − 1(i) 的递推公式得

在前向算法和后向算法中，给每一个 t 时刻的隐含状态结点定义了实际的物理含义，即 α_t(i), β_t(i) 两个中间变量分别从两边进行有向加权和有向边汇聚，形成一种递归结构，并且不断传播至两端，对任意 t = 1, t = T − 1 时刻，分别进行累加就能求得 P(O|λ)

2.4 概率与期望的计算

利用前向概率和后向概率，可以得到关于单个状态和两个状态概率的计算公式。

1.给定模型 λ 和观测 O ，在时刻 t 处于状态 q_i 的概率， 记

γ_t(i) = P(i_t = q_i|O, λ)

可以通过前向后向概率计算，

由前向概率 α_t(i) 和后向概率 β_t(i) 定义可知, α_t(i)β_t(i) 为在 HMM   λ 下，由前向和后向算法导出同一个中间节点 S ， 且 t 时刻状态为 q_i 的概率。

α_t(i)β_t(i) = P(i_t = q_i, O|λ)

于是有

2.给定模型 λ 和观测 O ,在时刻 t 处于状态 q_i 且在时刻 t + 1 处于状态 q_j 的概率：

ξ_t(i, j) = P(i_t = q_i, i_t + 1 = q_j|O, λ)

通过前向后向概率计算:

而 ξ_t(i, j) ,其物理含义：从 t 时刻出发由前向算法导出的中间节点 S_i 和从 t + 1 时刻出发，由后向算法导出的中间节点 S_j ,且节点 S_i, S_j 中间还有一条加权有向边的关系 a_ijb_j(O_t + 1) ，如下图:

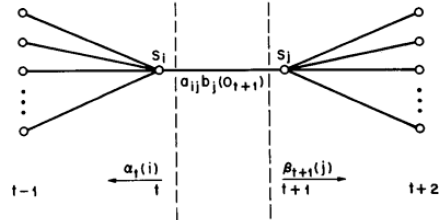
P(i_t = q_i, i_t + 1 = q_j, O|λ) = α_t(i)a_ijb_j(O_t + 1)β_t + 1(j)

所以

3.将 γ_t(i) 和 ξ_t(i, j) 对各个时刻 t 求和,可以得到一些有用的期望值:

(1)在观测 O 下状态 i 出现的期望

(2)在观测 O 下由状态 i 转移的期望

(3)在观测 O 下由状态 i 转移到状态 j 的期望值

3. 学习算法

3.1 监督学习算法

假设已给训练数据包含 S 个长度相同的观测序列和对应的状态序列

{(O₁, I₁), (O₂, I₂), ⋯, (O_S, I_S)}

那么可以利用极大似然估计法来估计 HMM 的参数:

1.转移概率 a_ij 的估计

设样本中时刻 t 处于状态 i 时刻 t + 1 转移到状态 j 的频数为 A_ij ,那么状态转移概率 a_ij 的估计是

2.观测概率 b_j(k) 的估计

设样本中状态为 j 并观测为 k 的频数是 B_jk ,那么状态为 j 观测为 k 的概率 b_j(k) 的估计是

3.初始状态概率 π_i 的估计 π̂_i 为 S 个样本中初始化状态为 q_i 的频率

由于监督学习需要使用训练数据，而人工标注训练数据代价很高，有时就会用非监督学习的方法。

3.2 Baum-Welch算法

假设给定训练数据只包含 S 个长度为 T 的观测序列

{O₁, O₂, ⋯, O_S}

而没有对应的状态序列，目标是学习隐马尔科夫模型 λ = (A, B, π) 的参数。将观测序列数据看作观测数据 O ，状态序列数据看作不可观测的隐数据 I ，那么 HMM 事实上是一个含有隐变量的概率模型

P(O|λ) = ∑_IP(O|I, λ)P(I|λ)

它的参数学习可以由 EM 算法实现。

1.确定完全数据的对数似然函数

所有观测数据写成 O = (o₁, o₂, ⋯, o_T) ，所有隐数据写成 I = (i₁, i₂, ⋯, i_T) ，完全数据是 (O, I) = (o₁, o₂, ⋯, o_T, i₁, i₂, ⋯, i_T) 。完全数据的对数似然函数是

log P(O, I|λ)

2. EM 算法的 E 步: 求 Q 函数

其中， 是 HMM 参数的当前估计值， λ 是要极大化的 HMM 参数，对于 λ 来说

为常数因子，可省略。

P(O, I|λ) = π_i1b_i1(o₁)a_i1i2b_i2(o₂)⋯a_{iT − 1iT}b_iT(o_T)

于是有:

式中求和都是对所有训练数据的序列总长度 T 进行的。

3. EM 算法的 M 步：极大化 Q 函数求模型参数 A, B, π

由于要极大化的参数在 Q 函数中单独地出现在3个项中，所以只需对各项分别极大化

(1)推导出的 Q 函数中的第一项可写成

注意到 π_i 满足约束条件 ，利用拉格朗日乘子法，写出拉格朗日函数:

对其求偏导，并令结果为 0

得

对 i 求和得到 γ

则 π_i 为

(2)推导出的 Q 函数的第二项可以写成

类似第一项，应用具有约束条件 的拉格朗日乘子法可以求出

(3)推导出的 Q 函数的第三项为：

同样用拉格朗日乘子法，约束条件是 .注意只有在 o_t = v_k 时 b_j(o_t) 对 b_j(k) 的偏导数才不为 0 ，以 I(o_t = v_k) 表示，求得

3.3 Baum-Welch模型参数估计公式

由

ξ_t(i, j) = P(i_t = q_i, i_t + 1 = q_j|O, λ)

可将上节估计出的参数写成:

π_i = γ₁(i)

以上三个结果就是 Baum-Welch 算法，它是 EM 算法在 HMM 学习中的具体实现，由 Baum 和 Welch 提出。

Baum-Welch 算法流程

输入: 观测数据 O = (o₁, o₂, ⋯, o_T) ;

输出: HMM 参数

(1)初始化

对 n = 0 ,选取 a_ij⁽⁰⁾, b_j(k)⁽⁰⁾, π_i⁽⁰⁾ ，得到模型 λ⁽⁰⁾ = (A⁽⁰⁾, B⁽⁰⁾, π⁽⁰⁾) .

(2)递推。 对 n = 1, 2, ⋯,

π_i^(n + 1) = γ₁(i)

右端各值按观测 O = (o₁, o₂, ⋯, o_T) 和模型 λ⁽ⁿ⁾ = (A⁽ⁿ⁾, B⁽ⁿ⁾, π⁽ⁿ⁾) 计算。

3. 终止，得到模型参数 λ^(n + 1) = (A^(n + 1), B^(n + 1), π^(n + 1))

4. 预测算法

4.1 近似算法

近似算法思想是，在每个时刻 t 选择在该时刻最有可能出现的状态i_t^*,从而得到一个状态序列I^* = (i₁^*, i₂^*, ⋯, i_T^*),将它作为预测的结果。

给定 HMM   λ 和观测序列 O ，在时刻 t 处于状态 q_i 的概率 γ_t(i) 是

在每一时刻 t 最有可能的状态i_t^*是

i_t^* = arg max_{1 ≤ i ≤ N}[γ_t(i)], t = 1, 2, ⋯, T

而得到状态序列I^* = (i₁^*, i₂^*, ⋯, i_T^*).

近似算法的优点是计算简单，其缺点是不能保证预测的状态序列整体是最有可能的状态序列，因为预测的状态序列可能有实际不发生的部分。事实上，上述方法得到的状态序列中有可能存在转移概率为 0 的相邻状态，即对某些 i, j, a_ij = 0 时，尽管如此，近似算法仍然是有用的。

4.2 维特比算法

维特比算法是用动态规划解 HMM 的预测问题，用动态规划(Dynamic Programming)求概率最大路径。这时一条路径对应一个状态序列。

根据动态规划原理，最优路径具有如下特性:如果最优路径在时刻 t 通过结点i_t^*,那么这一路径从结点i_t^*到终点i_T^*的部分路径，对于从i_t^*到i_T^*的所有可能的部分路径来说，必须是最优的。因为如果从i_t^*到i_T^*有另一条更好的部分路径存在，那么把它和从i₁^*到i_t^*的部分路径连接起来，就会形成一条比原来更优的路径，这是矛盾的。依据这一原理，我们只需从时刻 t = 1 开始，递推地计算在时刻 t 状态为 i 的各条部分路径的最大概率，直至得到时刻 t = T 状态为 i 的各条路径的最大概率。时刻 t = T 的最大概率即为最优路径的概率P^*,最优路径的终结点i_T^*也同时得到。之后，为了找出最优路径的各个结点，从终结点i_T^*开始，由后向前逐步求得结点i_T − 1^*, ⋯, i₁^*，得到最优路径I^* = (i₁^*, i₂^*, ⋯, i_T^*).以上即为维特比算法。

首先导入两个变量 δ 和 ψ .定义在时刻 t 状态为 i 的所有单个路径 (i₁, i₂, ⋯, i_t) 中概率最大值为

δ_t(i) = max_{i1, i2, ⋯, it − 1}P(i_t = i, i_t − 1, ⋯, i₁, o_t, ⋯, o₁|λ),   i = 1, 2, ⋯, N

由定义可得变量 δ 的递推公式:

δ_t + 1(i) = max_{i1, i2, ⋯, it}P(i_t + 1 = i, i_t, ⋯, i₁, o_t + 1, ⋯, o₁|λ) = max_{1 ≤ j ≤ N}[δ_t(j)a_ji]b_i(o_t + 1),   t = 1, 2, ⋯, T − 1

定义在时刻 t 状态为 i 的所有单个路径 (i₁, i₂, ⋯, i_t − 1, i) 中概率最大的路径的第 t − 1 个结点为

ψ_t(i) = arg max_{1 ≤ j ≤ N}[δ_t − 1(j)a_ji],   i = 1, 2, ⋯, N

维特比算法流程

输入：模型 λ = (A, B, π) 和观测 O = (o₁, o₂, ⋯, o_T) ;

输出：最优路径

I^* = (i₁^*, i₂^*, ⋯, i_T^*)

(1)初始化

δ₁(i) = π_ib_i(o₁),   ψ₁(i) = 0,   i = 1, 2, ⋯, N

(2)递推。对 t = 2, 3, ⋯, T

δ_t(i) = max_{1 ≤ j ≤ N}[δ_t − 1(j)a_ji]b_i(o_t),   i = 1, 2, ⋯, N

ψ_t(i) = arg max_{1 ≤ j ≤ N}[δ_t − 1(j)a_ji],   i = 1, 2, ⋯, N

(3)终止

P^* = max_{1 ≤ i ≤ N}δ_T(i)

i_T^* = arg max_{1 ≤ i ≤ N}[δ_T(i)]

(4)最优路径回溯。对 t = T − 2, T − 2, ⋯, 1

i_t^*ψ_t + 1(i_t + 1^*)

求得最优路径

I^* = (i₁^*, i₂^*, ⋯, i_T^*)

例

考虑盒子和球模型 λ = (A, B, π) ，状态集合

Q = {1, 2, 3}

观测集合

V = {Red, White}

设 T = 3, O = (Red, White, Red) ,试求最优状态序列，即最优路径

I^* = (i₁^*, i₂^*, i₃^*)

解 如下图，

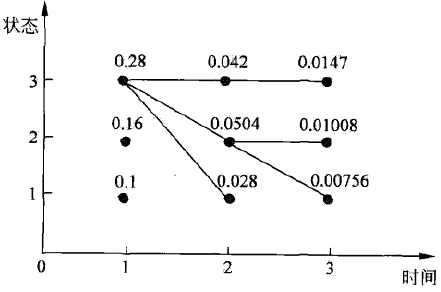
要在所有可能路径中选择一个最优路径，按以下处理:

(1)初始化。在 t = 1 时，对每一个状态 i, i = 1, 2, 3 ，求状态为 i 观测 o₁ 为红的概率，记为 δ₁(i) ,则

δ₁(i) = π_ib_i(o₁) = π_ib_i(Red)

代入实际数据

δ₁(1) = 0.10,     δ₁(2) = 0.16,     δ₁(3) = 0.28

记 ψ₁(i) = 0

(2)在 t = 2 时，对每一个状态 i, i = 1, 2, 3 ，求在 t = 1 时状态为 j 观测为红并且在 t = 2 时状态为 i 观测为 o₂ 为白的路径最大概率，记为 δ₂(i) ,则

δ₂(i) = max_{1 ≤ j ≤ 3}[δ(j)a_ji]b_i(o₂)

同时，对每个状态 i ，记录概率最大路径的前一个状态 j :

ψ₂(i) = arg max_{1 ≤ j ≤ 3}[δ₁(j)a_ji]

计算：

同样，在 t = 3 时，

(3)以P^*表示最优路径的概率，则

P^* = max_{1 ≤ j ≤ 3}δ₃(i) = 0.0147

最优路径的终点是i₃^*：

i₃^* = arg max_i[δ₃(i)] = 3

(4)由最优路径的终点i₃^*,逆向找到i₂^*, i₁^*:

t = 2,       i₂^* = ψ₃(i₃^*) = ψ₃(3) = 3

t = 1,       i₁^* = ψ₃(i₂^*) = ψ₂(3) = 3

于是求得最优路径，即最优状态序列

I^* = (i₁^*, i₂^*, i₃^*) = (3, 3, 3)

参考

1. 周志华 《机器学习》
2. 隐马尔可夫模型
3. 隐马尔可夫模型之Baum-Welch算法详解
4. 隐马尔可夫模型（HMM）攻略