推荐算法--双塔模型

一、双塔模型

双塔模型（two-tower）也叫 DSSM，是推荐系统中最重要的召回通道，没有之一。这节课的内容是双塔模型的结构、训练方式。

双塔模型有两个塔：用户塔、物品塔。两个塔各输出一个向量，作为用户、物品的表征。两个向量的內积或余弦相似度作为对兴趣的预估。

用户塔：

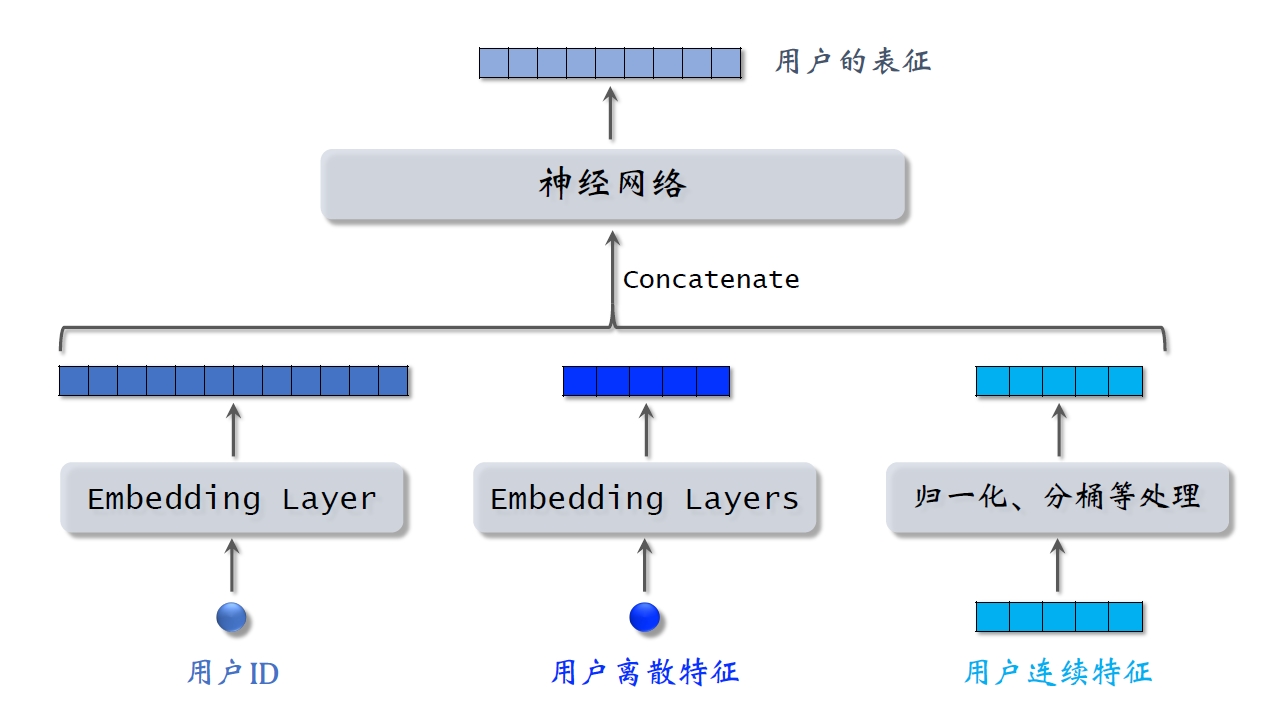
物品塔:

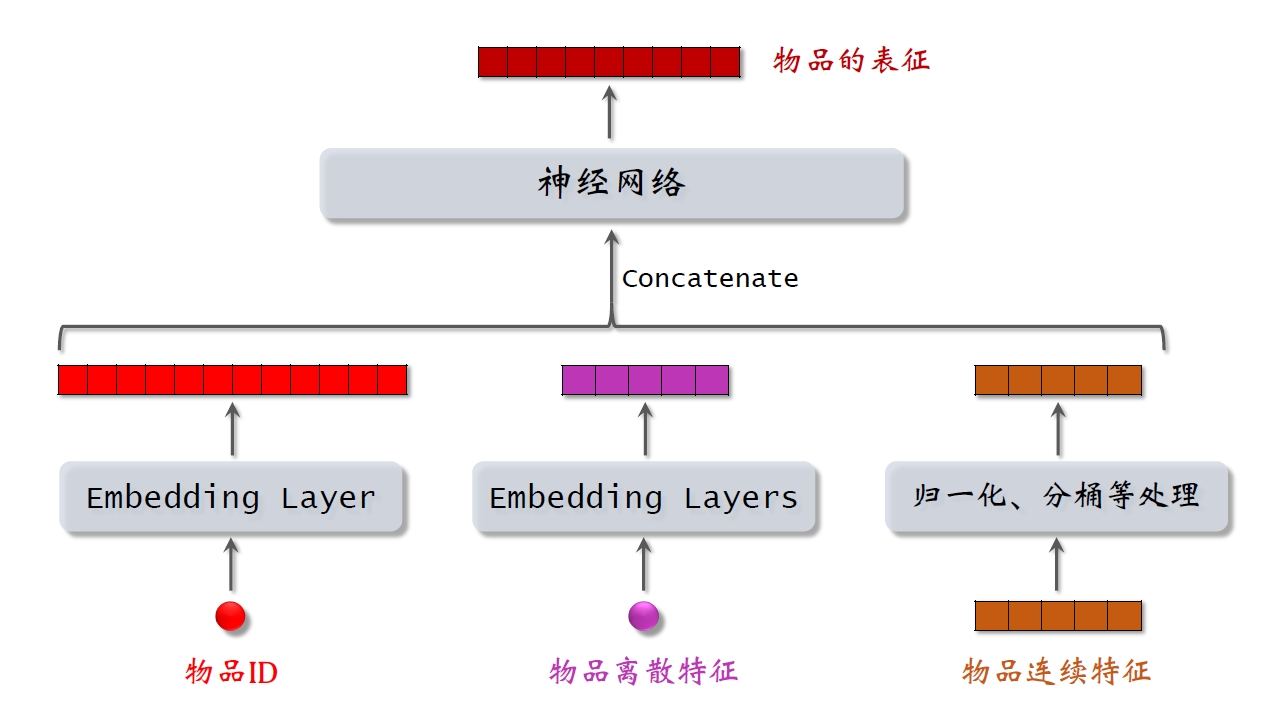
双塔模型：

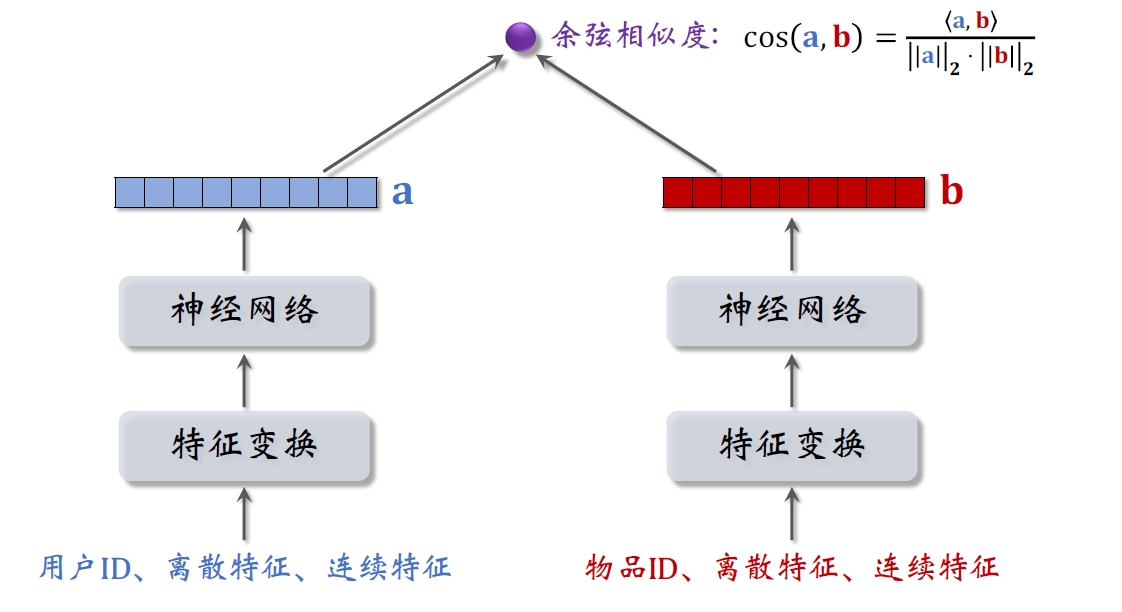
二、双塔模型的训练

双塔模型训练方式有以下几种：

• Pointwise：独⽴看待每个正样本、负样本，做简单的⼆元分类。
• Pairwise：每次取⼀个正样本、⼀个负样本^[1]。
• Listwise：每次取⼀个正样本、多个负样本^[2]。

2.1 正负样本的选择

正样本：曝光⽽且有点击。

2.1.1 如何选择负样本？

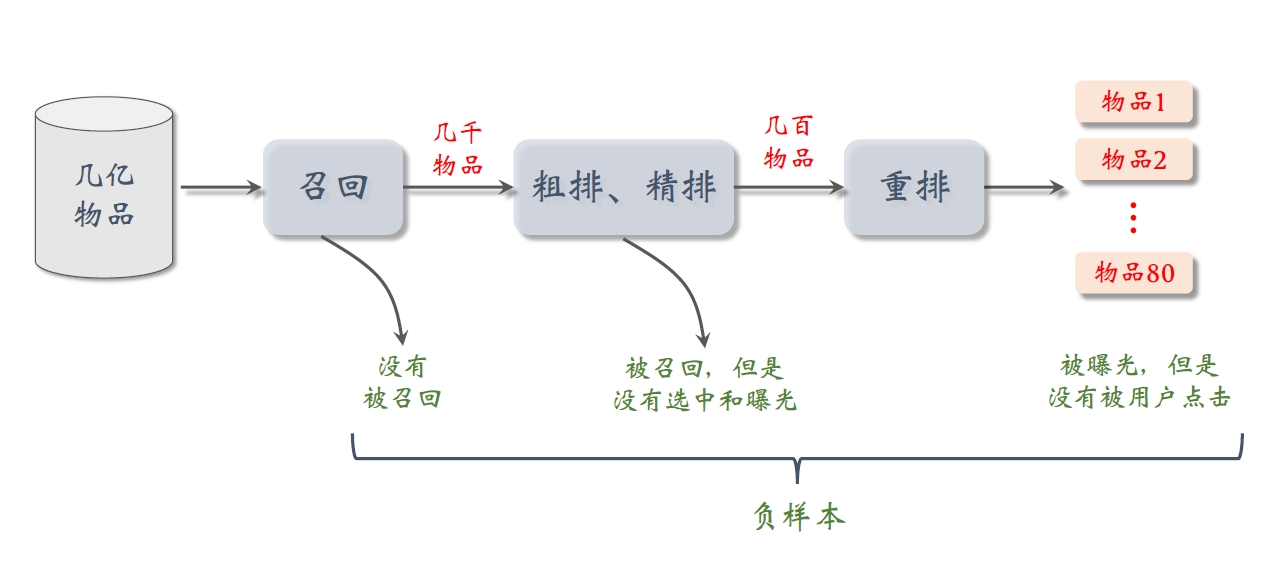
1. 简单负样本：全体物品

未被召回的物品，⼤概率是⽤户不感兴趣的。推荐系统中被召回的物品是少数的，因此未被召回的物品约等于全体物品。从全体物品中做抽样，作为负样本。

• 均匀抽样：对冷门物品不公平
  • 正样本⼤多是热门物品。
  • 如果均匀抽样产⽣负样本，负样本⼤多是冷门物品。
• ⾮均抽采样：⽬的是打压热门物品
  • 负样本抽样概率与热门程度（点击次数）正相关。
  • 抽样概率 ∝ (点击次数)^0.75(0.75为经验值)

2. 简单负样本：Batch内负样本

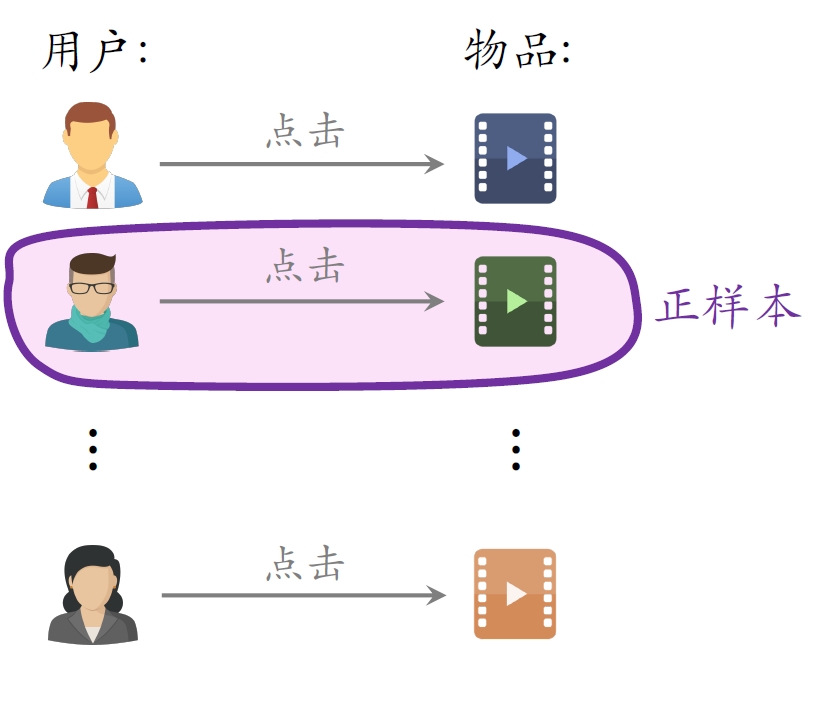
• ⼀个batch内有n个正样本。
• ⼀个⽤户和n − 1个物品组成负样本。
• 这个batch内⼀共有n(n − 1)个负样本。
• 都是简单负样本。（因为第⼀个⽤户不喜欢第⼆个物品。）

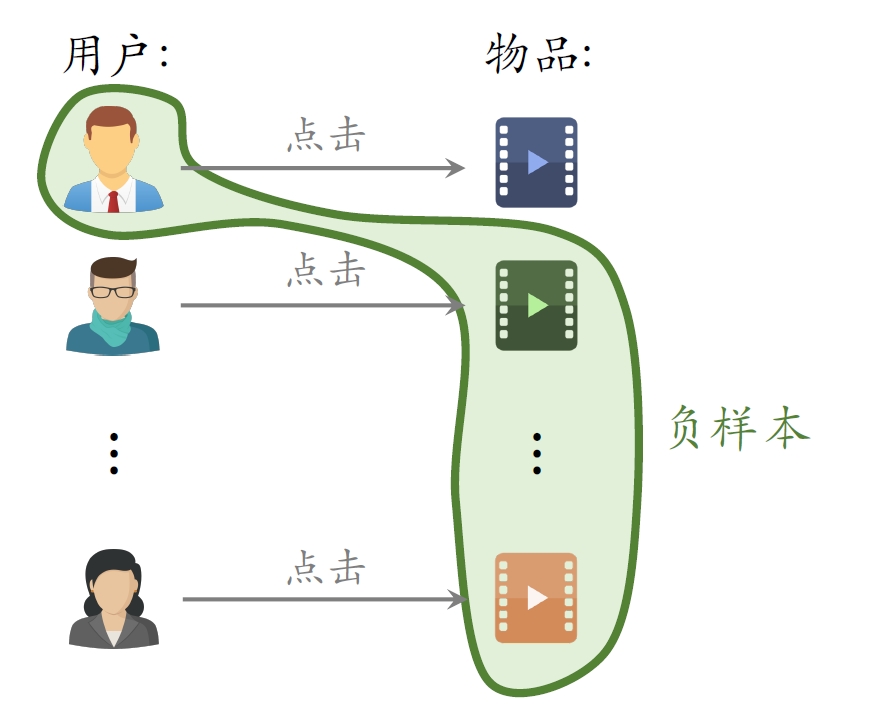
• ⼀个物品出现在batch内的概率 ∝ 点击次数
• 物品成为负样本的概率本该是 ∝ (点击次数)^0.75，但在这⾥是 ∝ 点击次数
• 热门物品成为负样本的概率过⼤。

纠正热门物品成为负样本的概率过⼤的问题^[2]

• 物品i被抽样到的概率：p_i ∝ 点击次数
• 预估⽤户对物品i的兴趣：cos (a, b_i)
• 做训练的时候，调整为：cos (a, b_i) − log p_i

3. 困难负样本

• 被粗排淘汰的物品（⽐较困难）。
• 精排分数靠后的物品（⾮常困难）。

对正负样本做⼆元分类：

• 全体物品（简单）分类准确率⾼。
• 被粗排淘汰的物品（⽐较困难）容易分错。
• 精排分数靠后的物品（⾮常困难）更容易分错。

2.1.2 训练数据

• 混合⼏种负样本。
• 50%的负样本是全体物品（简单负样本）。
• 50%的负样本是没通过排序的物品（困难负样本）。

召回的⽬标：快速找到⽤户可能感兴趣的物品。

• 全体物品（easy ）：绝⼤多数是⽤户根本不感兴趣的。
• 被排序淘汰（hard）：⽤户可能感兴趣，但是不够感兴趣。
• 有曝光没点击（没⽤）：⽤户感兴趣，可能碰巧没有点击。(可以作为排序的负样本，不能作为召回的负样本)

2.1.3 总结

• 正样本：曝光⽽且有点击。
• 简单负样本：
  • 全体物品。
  • batch内负样本。
• 困难负样本：被召回，但是被排序淘汰。
• 曝光、但是未点击的物品做召回的负样本。

2.2 Pointwise训练

• 把召回看做⼆元分类任务。
• 对于正样本，⿎励cos (a, b)接近+1。
• 对于负样本，⿎励cos (a, b)接近-1。
• 控制正负样本数量为1: 2或者1: 3。(经验)

2.3 Pairwise训练

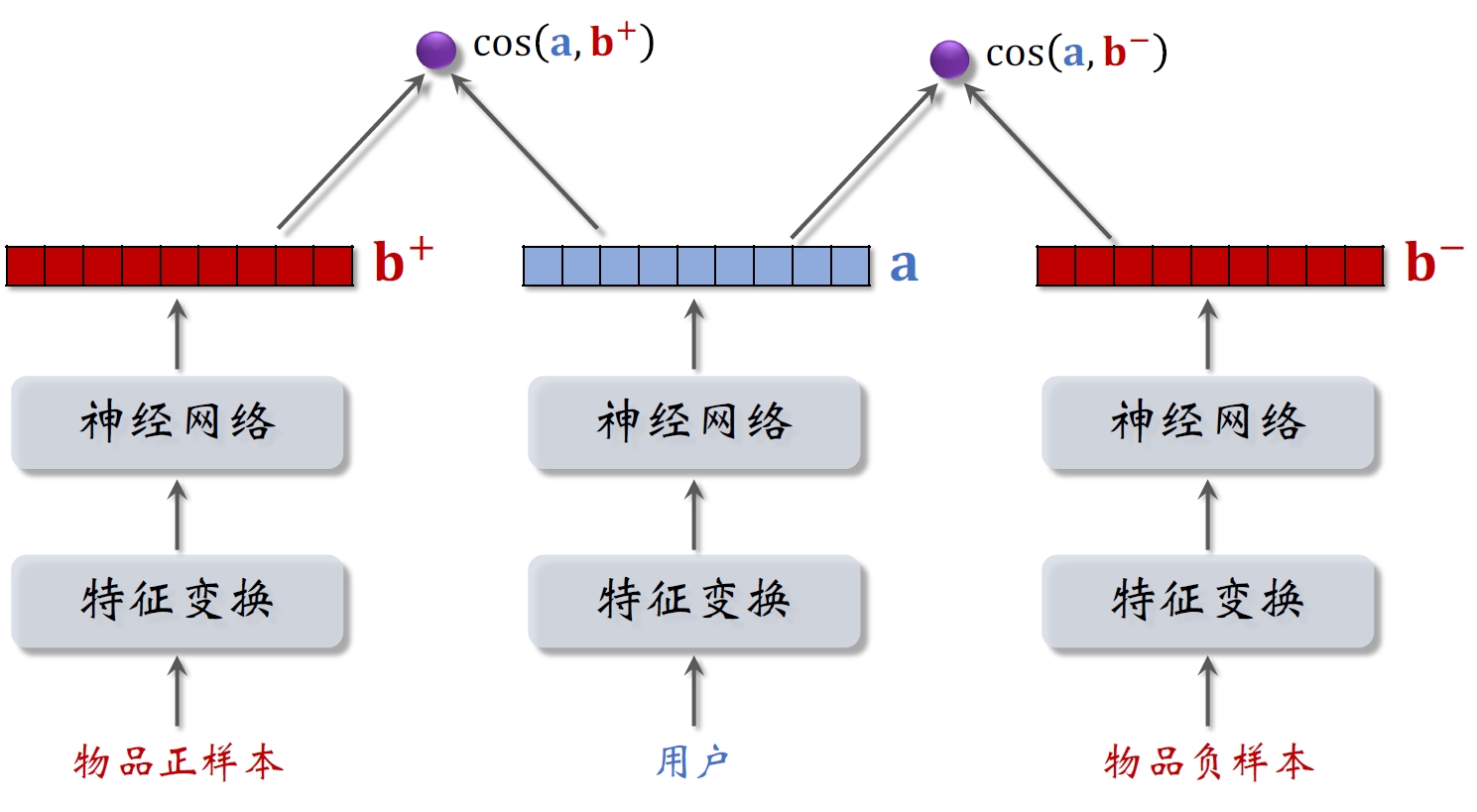
上图中正负样本的物品塔是相同的，共用参数。

基本想法：⿎励cos (a, b⁺)大于cos (a, b⁻)，差越大越好

• 如果cos (a, b⁺)⼤于cos (a, b⁻) + m，则没有损失。
• 否则，损失等于 cos (a, b⁻) + m − cos (a, b⁺)

Triplet hinge loss:

L(a, b⁺, b⁻) = max {0, cos (a, b⁻) + m − cos (a, b⁺)}

Triplet logistic loss:

L(a, b⁺, b⁻) = log (1 + exp [σ ⋅ (cos (a, b⁻) − cos (a, b⁺))])

2.4 Listwise训练

• ⼀条数据包含：
  • ⼀个⽤户，特征向量记作a
  • ⼀个正样本，特征向量记作b⁺
  • 多个负样本，特征向量记作b₁⁻, ⋯, b_n⁻
• 鼓励cos (a, b⁺)尽量大
• 鼓励cos (a, b₁⁺−), ⋯, cos (a, b_n⁺−)尽量小

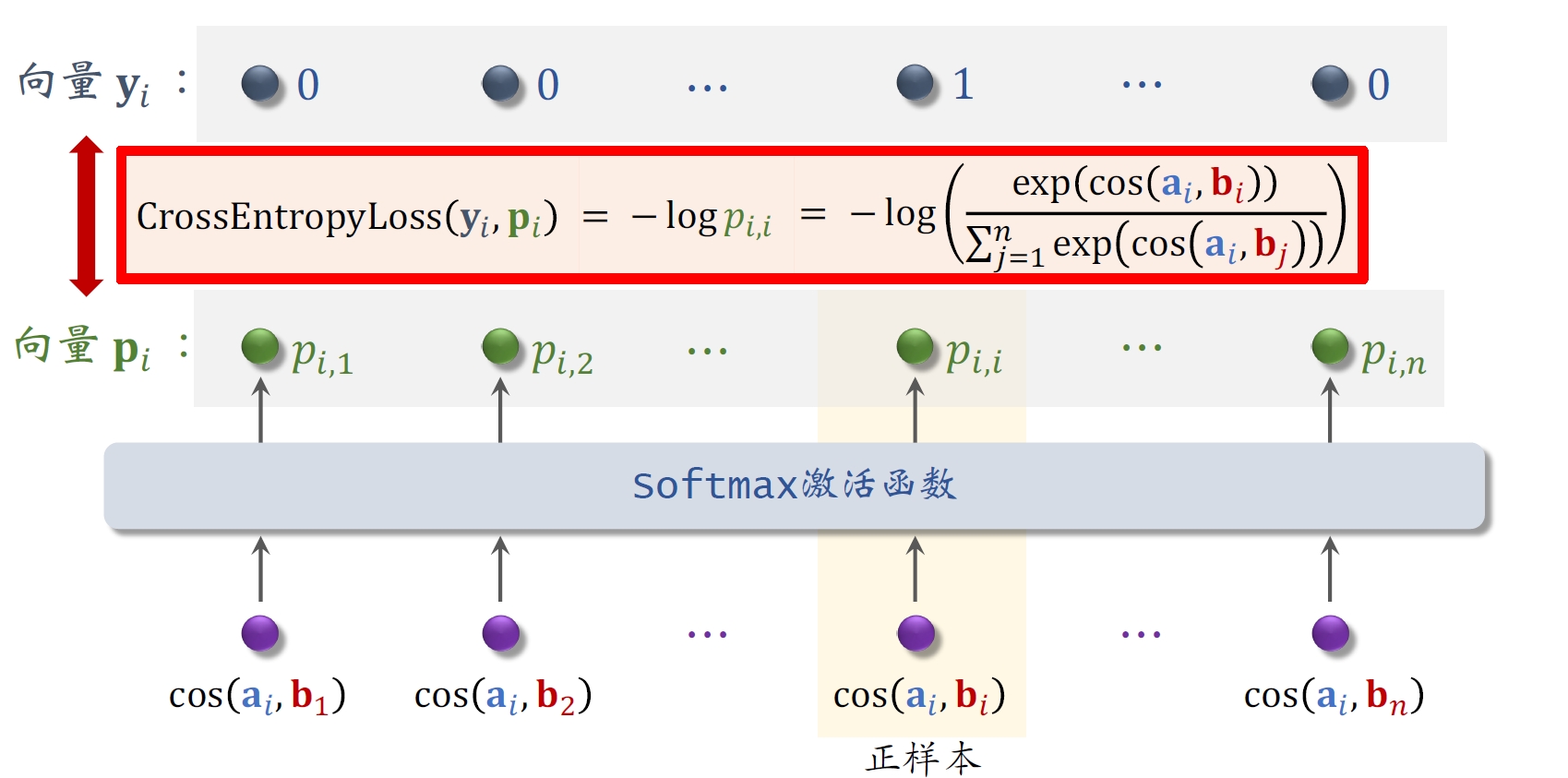
• 从点击数据中随机抽取𝑛 个⽤户—物品⼆元组，组成⼀个batch。
• 对应用户i双塔模型的损失函数（纠偏）：

• 做梯度下降，减⼩损失函数：

2.5 总结

• ⽤户塔、物品塔各输出⼀个向量。
• 两个向量的余弦相似度作为兴趣的预估值。
• 三种训练⽅式：
  • Pointwise：每次⽤⼀个⽤户、⼀个物品（可正可负）。
  • Pairwise：每次⽤⼀个⽤户、⼀个正样本、⼀个负样本。
  • Listwise：每次⽤⼀个⽤户、⼀个正样本、多个负样本。

三、线上召回

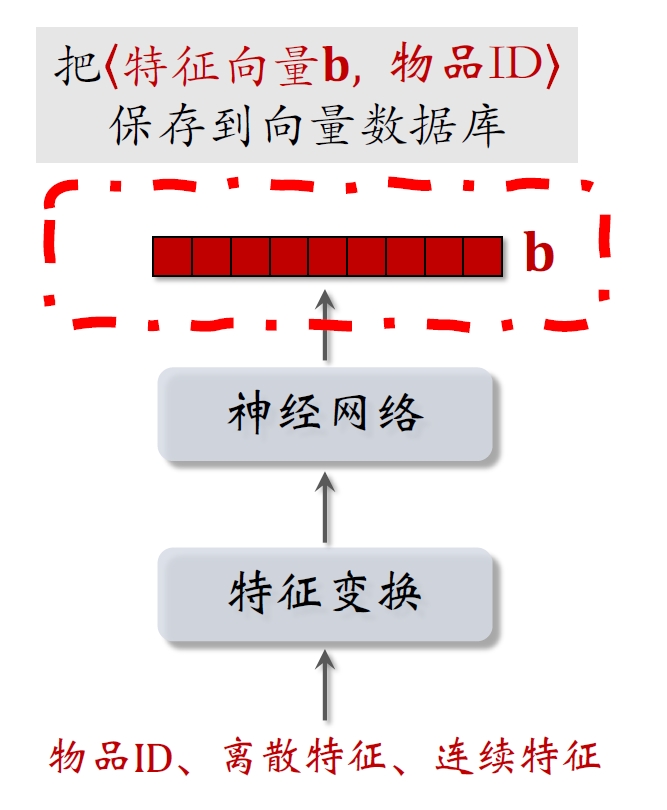
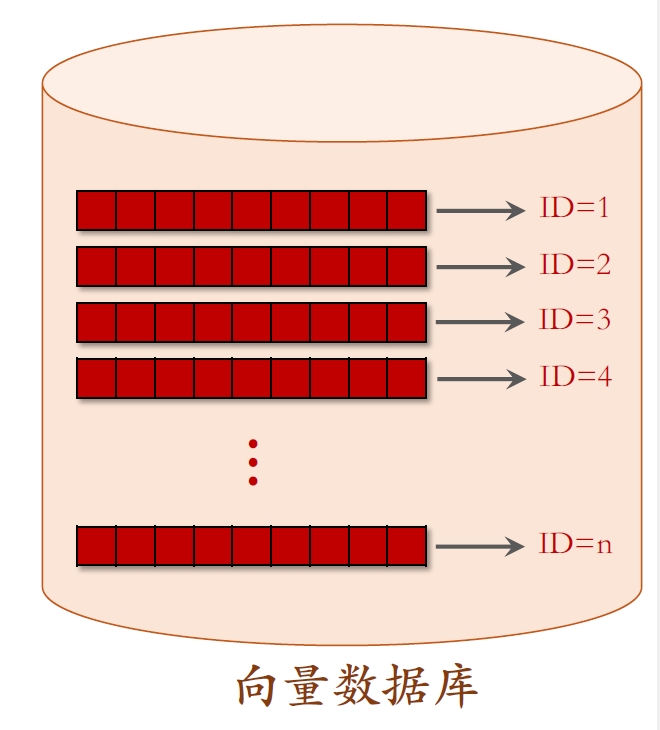
离线存储：把物品向量b存⼊向量数据库。

1. 完成训练之后，⽤物品塔计算每个物品的特征向量b。
2. 把物品向量b存⼊向量数据库(Faiss,Scann,Nilvus)
3. 向量数据库建索引，以便加速最近邻查找。

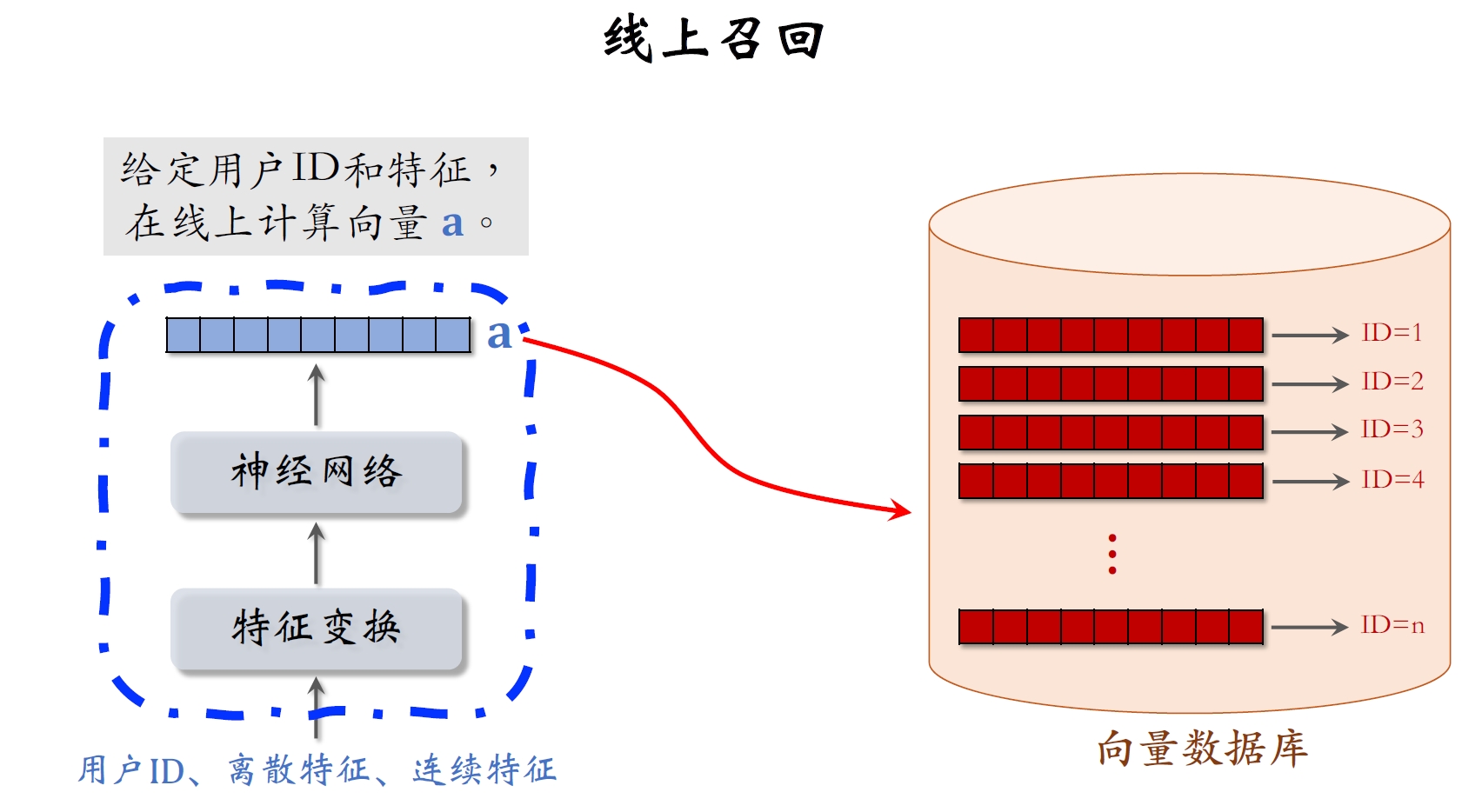
线上召回：查找⽤户最感兴趣的k个物品。

1. 给定⽤户ID和画像，线上⽤神经⽹络算⽤户向量a。
2. 最近邻查找：
   • 把向量a作为query，调⽤向量数据库做最近邻查找。
   • 返回余弦相似度最⼤的k个物品，作为召回结果。

为什么事先存储物品向量b，线上现算⽤户向量a？

• 每做⼀次召回，⽤到⼀个⽤户向量a,⼏亿物品向量b。（线上算物品向量的代价过⼤。）
• ⽤户兴趣动态变化，⽽物品特征相对稳定。（可以离线存储⽤户向量，但不利于推荐效果。）

四、模型更新

4.1 全量更新

全量更新：今天凌晨，⽤昨天全天的数据训练模型。

• 在昨天模型参数的基础上做训练。（不是随机初始化）
• ⽤昨天的数据，训练1 epoch，即每天数据只⽤⼀遍。
• 发布新的⽤户塔神经⽹络和物品向量，供线上召回使⽤。
• 全量更新对数据流、系统的要求⽐较低。

4.2 增量更新

增量更新：做online learning 更新模型参数。

• ⽤户兴趣会随时发⽣变化。
• 实时收集线上数据，做流式处理，⽣成TFRecord⽂件。
• 对模型做online learning，增量更新ID Embedding 参数。（不更新神经⽹络其他部分的参数。）
• 发布⽤户ID Embedding，供⽤户塔在线上计算⽤户向量。

4.3 全量更新vs 增量更新

问题：能否只做增量更新，不做全量更新？

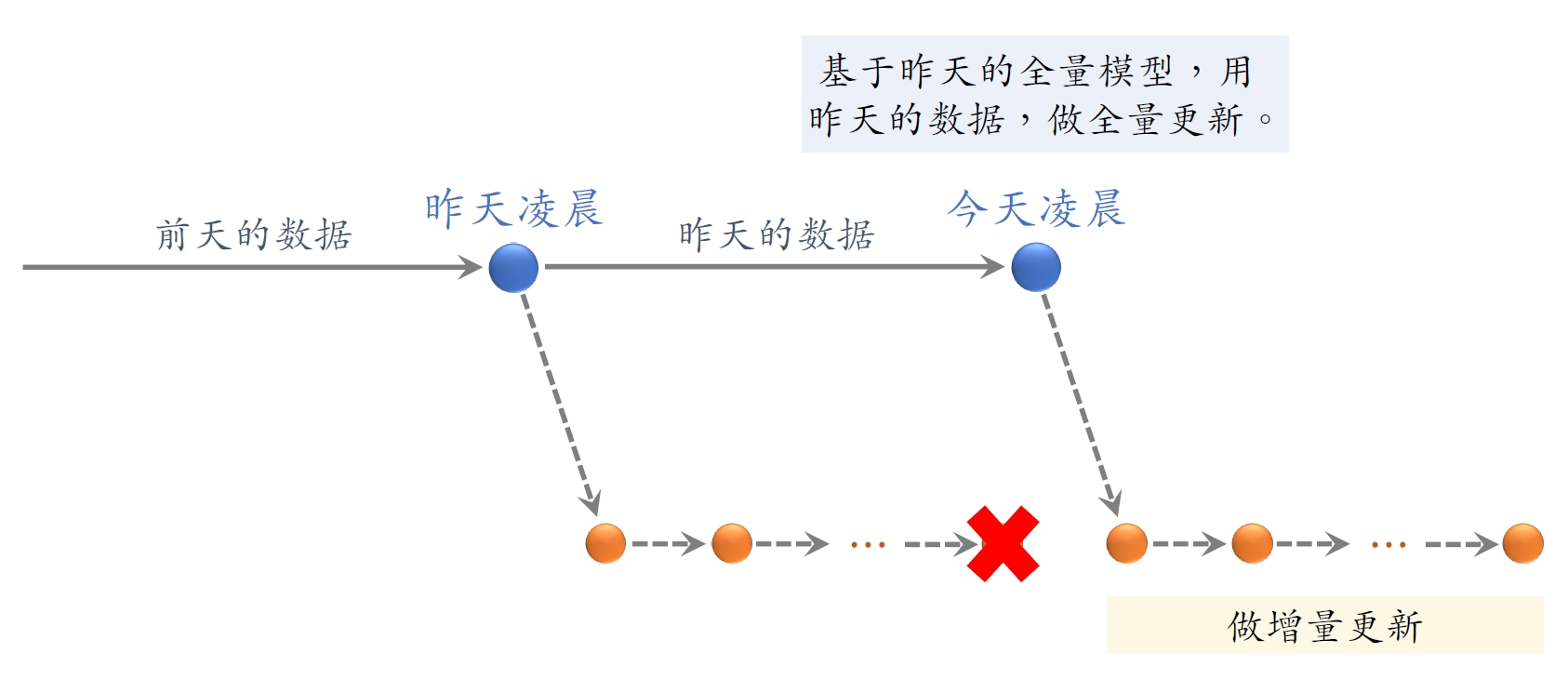
• ⼩时级数据有偏；分钟级数据偏差更⼤。
• 全量更新：random shuffle ⼀天的数据，做1 epoch训练。
• 增量更新：按照数据从早到晚的顺序，做1 epoch训练。
• 随机打乱优于按顺序排列数据，全量训练优于增量训练。

4.4 总结

• 全量更新：今天凌晨，⽤昨天的数据训练整个神经⽹络，做1 epoch的随机梯度下降。

• 增量更新：⽤实时数据训练神经⽹络，只更新IDEmbedding，锁住全连接层。

• 实际的系统：

  • 全量更新&增量更新相结合。
  • 每隔⼏⼗分钟，发布最新的⽤户ID Embedding，供⽤户塔在线上计算⽤户向量。

五、自监督学习

• 推荐系统的头部效应严重：

  • 少部分物品占据⼤部分点击。
  • ⼤部分物品的点击次数不⾼。

• ⾼点击物品的表征学得好，长尾物品的表征学得不好。

• ⾃监督学习：做data augmentation，更好地学习长尾物品的向量表征^[3]。

• 物品i的两个向量表征b_i^′和b_i^′′有较⾼的相似度。

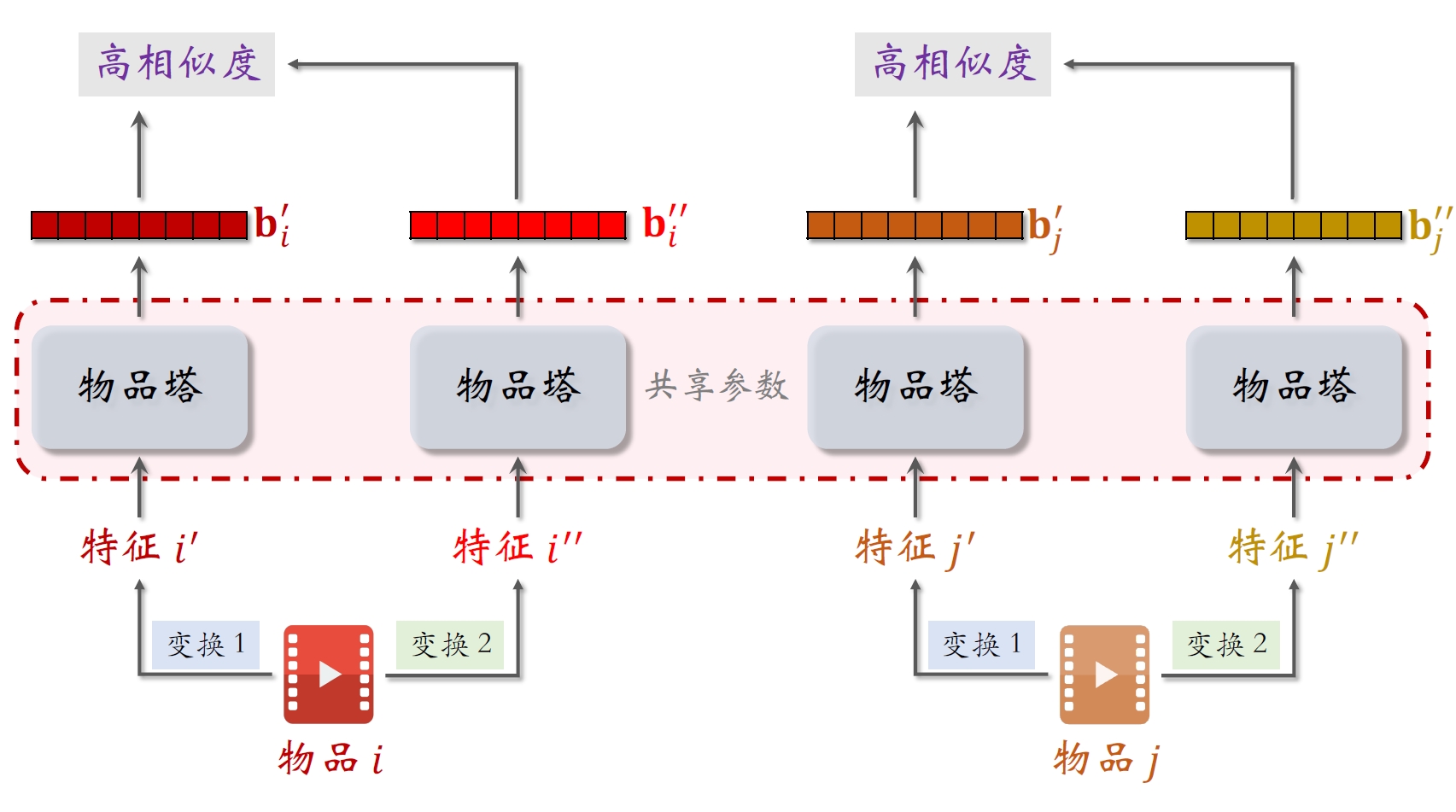
• 物品i和j的向量表征b_i^′和b_j^′′有较低的相似度。

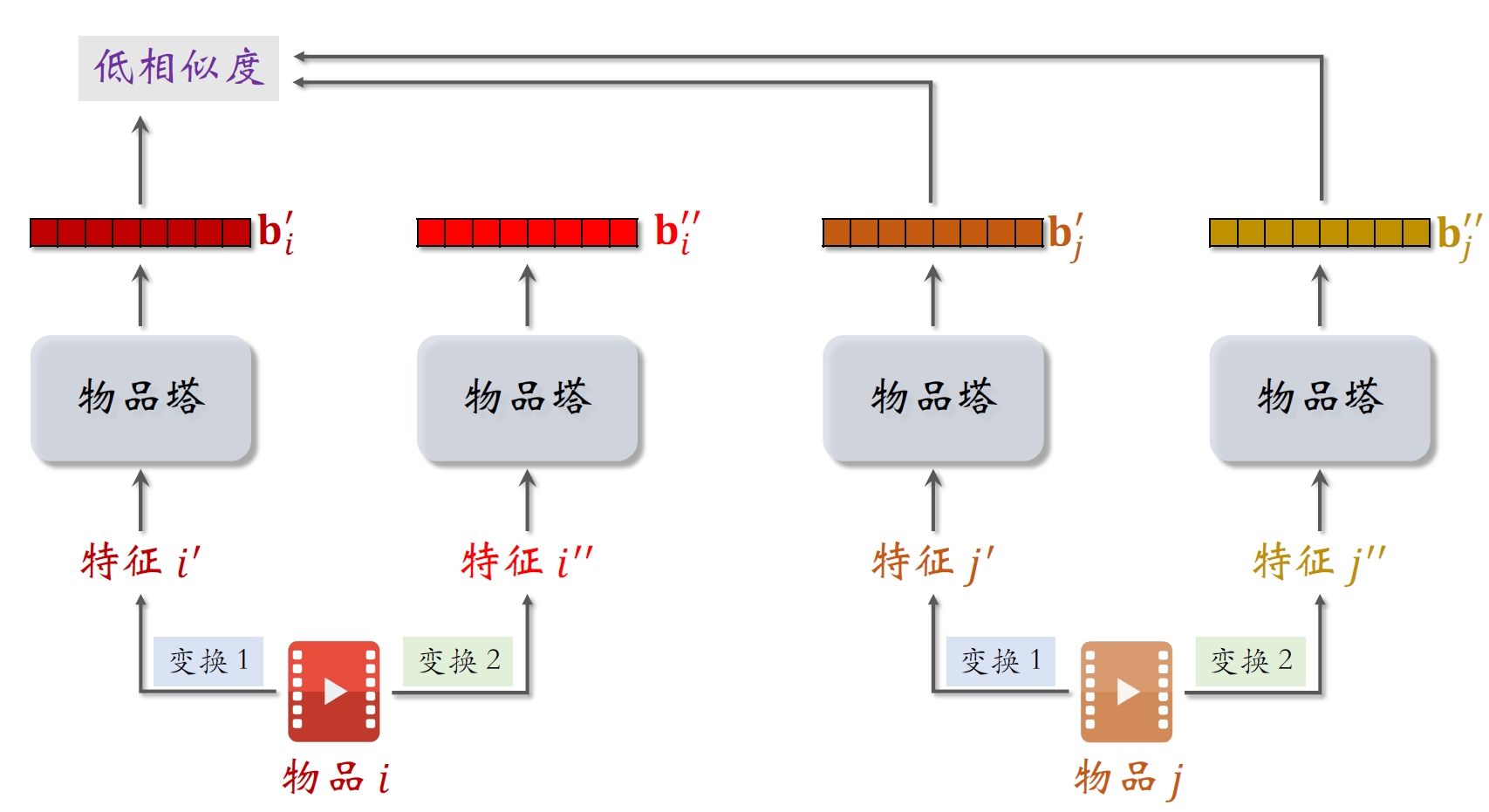
• ⿎励cos (b_i^′, b_i^′′)尽量大，cos (b_i^′, b_j^′′)尽量小

5.1 特征变换

特征变换：Random Mask

• 随机选⼀些离散特征（⽐如类⽬），把它们遮住。
• 例：
  • 某物品的类⽬特征是𝒰 = {数码, 摄影}
  • Mask 后的类⽬特征是𝒰^′ = {default}

特征变换：Dropout（仅对多值离散特征⽣效）

• ⼀个物品可以有多个类⽬，那么类⽬是⼀个多值离散特征。
• Dropout：随机丢弃特征中50%的值。
• 例：
  • 某物品的类⽬特征是𝒰 = {数码, 摄影}
  • Mask 后的类⽬特征是𝒰^′ = {摄影}

特征变换：互补特征（complementary）

• 假设物品⼀共有4种特征：ID，类⽬，关键词，城市
• 随机分成两组：{ID，关键词}和{类⽬，城市}
• {ID，default，关键词，default} → 物品表征
• { default，类⽬，default，城市} → 物品表征（⿎励两个向量相似）

特征变换：Mask⼀组关联的特征

• 受众性别：𝒰 = {男, 女, 中性}

• 类⽬：𝒱 = {美妆, 数码, 主球, 摄影, 科技, ⋯}

• u = 女和v = 美妆同时出现的概率p(u, v)大

• u = 女和v = 数码同时出现的概率p(u, v)小

• p(u)：某特征取值为u的概率

  • p(男性) = 20%
  • p(女性) = 30%
  • p(中性) = 50%

• p(u, v)：某特征取值为u，另⼀个特征取值为v，同时发⽣的概率。

  • p(女性, 美妆) = 3%
  • p(女性，数码) = 0.1%

• 离线计算特征两两之间的关联，⽤互信息（mutual information）衡量：

• 设⼀共有k种特征。离线计算特征两两之间MI，得到k × k的矩阵。
• 随机选⼀个特征作为种⼦，找到种⼦最相关的k/2种特征
• Mask种⼦及其相关的k/2种特征，保留其余的k/2种特征。

1. 好处：⽐random mask、dropout、互补特征等⽅法效果更好。
2. 坏处：⽅法复杂，实现的难度⼤，不容易维护。

5.2 训练模型

• 从全体物品中均匀抽样，得到m个物品，作为⼀个batch。
• 做两类特征变换，物品塔输出两组向量：b₁^′, b₂^′, ⋯, b_m^′和b₁^′′, b₂^′′, ⋯, b_m^′′
• 第i个物品的损失函数：

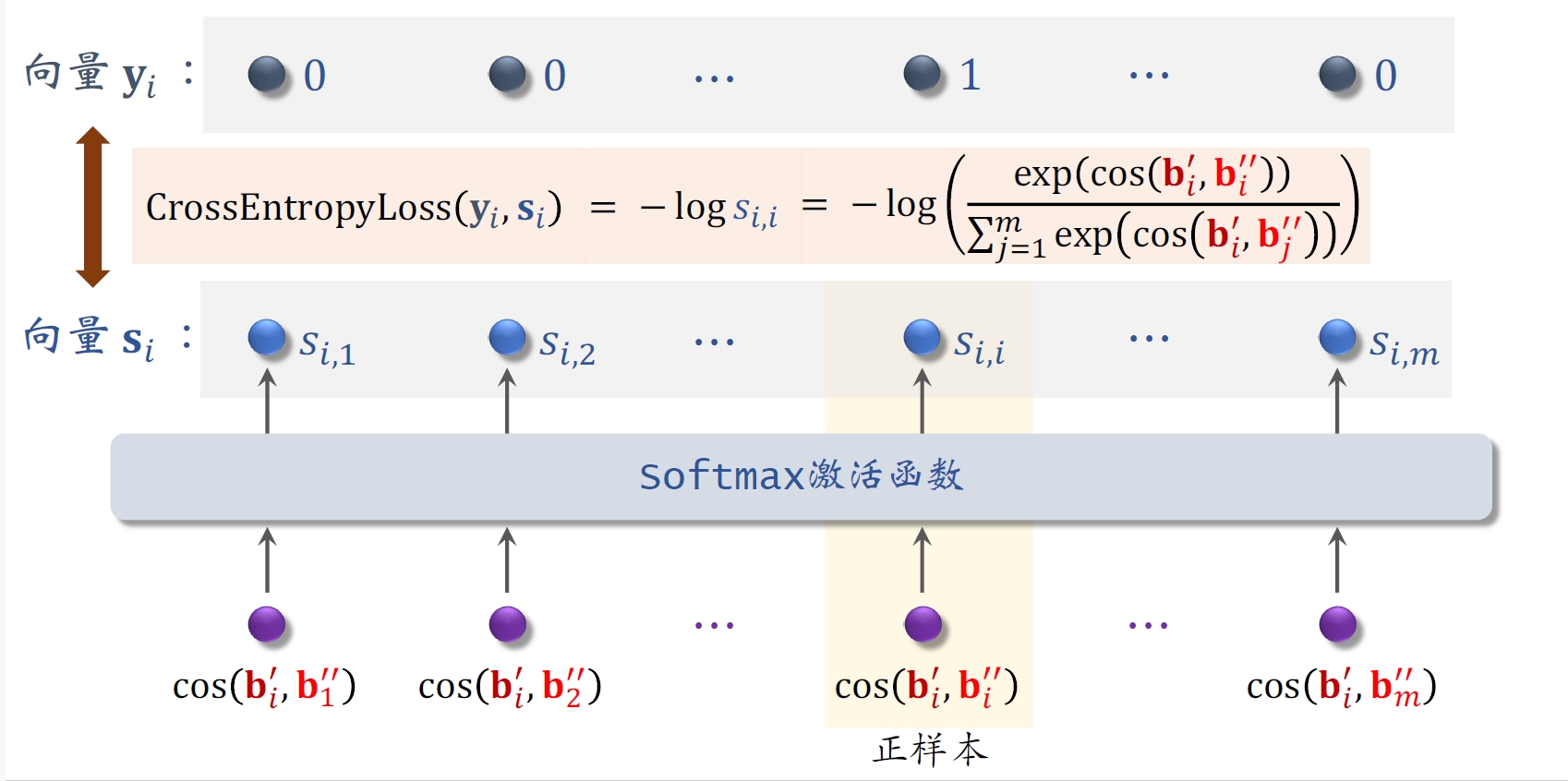
• ⾃监督学习的损失函数：

• 做梯度下降，减⼩⾃监督学习的损失：

5.3 总结

• 双塔模型学不好低曝光物品的向量表征。
• ⾃监督学习：
  • 对物品做随机特征变换。
  • 特征向量b_i^′和b_i^′′相似度高(相同物品)
  • 特征向量b_i^′和b_j^′′相似度低（不同物品）

训练

• 对点击做随机抽样，得到n对⽤户—物品⼆元组，作为⼀个batch。
• 从全体物品中均匀抽样，得到m个物品，作为⼀个batch。
• 做梯度下降，使得损失减⼩：

前半部分为双塔模型的损失，后半部分为自监督学习的损失,α为超参数

1. https://arxiv.org/abs/2006.11632 ↩︎
2. https://dl.acm.org/doi/abs/10.1145/3298689.3346996 ↩︎
3. https://arxiv.org/abs/2007.12865 ↩︎