Native Sparse Attention——DeepSeek 提出硬件级的稀疏注意力机制
论文:[2502.11089] Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention
一、简介
DeepSeek 团队最近(2025 年 2 月)提出的一种稀疏注意力机制,核心的创新在于:
- 智能信息分层:将文本压缩为粗粒度语义块、动态筛选关键片段,并结合局部滑动窗口,既保留全局理解又减少冗余计算;
- 硬件级优化:针对 GPU 的 Tensor Core 特性设计高效计算内核,在 64k 长度文本处理中实现最高 9 倍训练加速和11 倍解码加速;
- 原生可训练设计:支持端到端学习稀疏模式,避免传统方法「先训练后裁剪」的性能损失。实验证明,NSA 模型在通用理解、长文本检索和复杂数学推理任务中全面超越传统注意力模型,同时大幅降低算力成本。这一技术为长文档分析、代码生成和多轮对话等场景提供了更高效的底层支持,堪称大模型长文本处理的「瘦身加速器」。
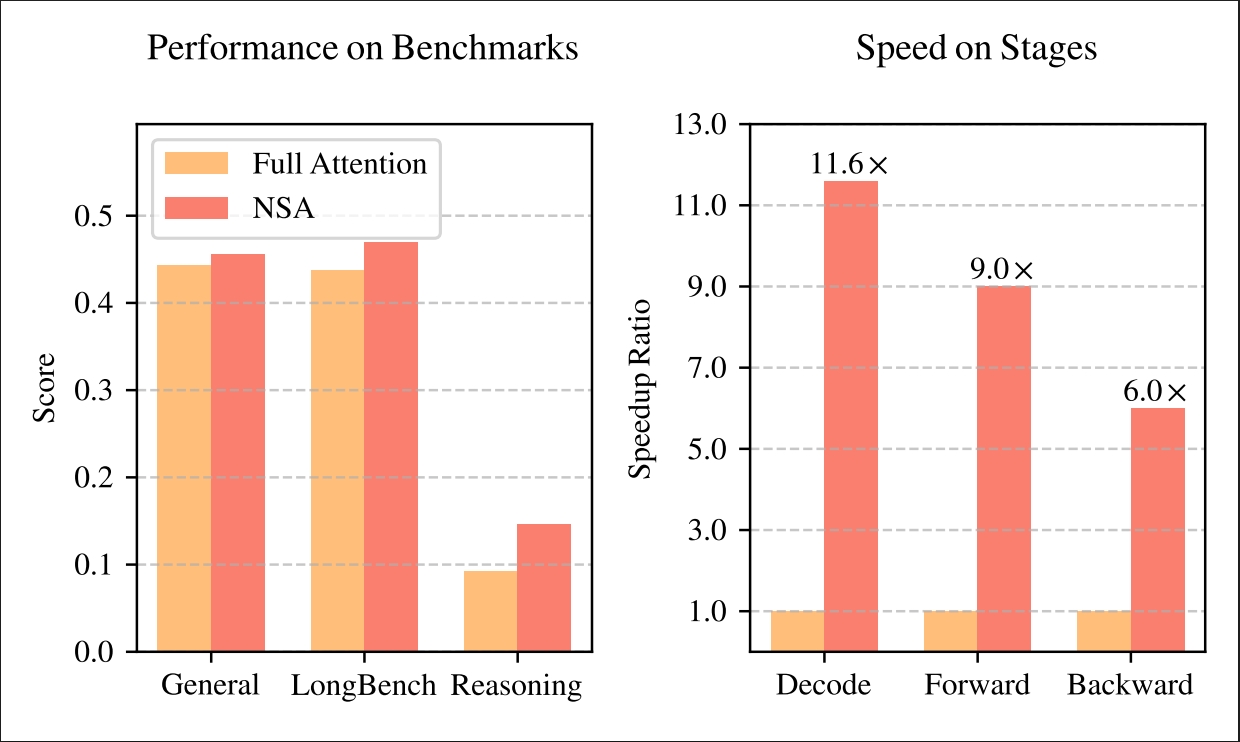
如图所示,实验表明,使用 NSA 预训练的模型在通用基准测试、长上下文任务和基于指令的推理方面,其性能维持或超过了全注意力(Full Attention)模型。同时,在处理 64k 长度序列时,NSA 在解码、前向传播和反向传播方面均比全注意力实现了显著的加速,验证了其在整个模型生命周期中的效率。
1.1 背景
- 长文本建模的重要性:随着大语言模型的发展,处理长文本 (例如,完整的代码库、长篇文档) 的能力变得越来越重要。这使得模型能够进行更深入的推理、代码生成和多轮对话。
- 传统 Attention 的瓶颈:传统的 Attention 机制的计算复杂度是序列长度的平方级别 (O(n2)),这使得处理长文本时计算成本非常高。
- 稀疏 Attention 的潜力:稀疏 Attention 是一种通过选择性地计算关键 query-key 对来降低计算开销,同时保持模型性能的方法。
1.2 相关研究
- KV-cache 优化:
问题:通常只关注推理阶段,缺乏对训练阶段的支持。在实际部署中,难以达到理论上的加速效果。
问题:包含非可训练的组件 (例如,k-means 聚类),阻碍了梯度反向传播。反向传播效率低,例如 HashAttention 需要加载大量的 token,导致内存访问不连续,无法充分利用硬件加速。
1.3 论文核心思路
- 核心思想:设计一种原生可训练的稀疏注意力架构 (NSA),通过层级化的 token 建模和硬件对齐的优化,实现高效的长文本建模。
- 灵感来源:
- Attention 的稀疏性:观察到 Attention score 存在内在的稀疏性,即只有少数 query-key 对是重要的。
- 硬件效率:充分利用现代 GPU 的特性 (例如,Tensor Core) 和 FlashAttention 的设计原则,实现高效的计算和内存访问。
- 主要创新:
- 硬件对齐的系统 (Hardware-aligned system):优化 blockwise 稀疏 Attention,充分利用 Tensor Core 和内存访问,确保算法的算术强度 (arithmetic intensity) 平衡。
- 训练感知的设计 (Training-aware design):通过高效的算法和反向传播算子,实现稳定的端到端训练。
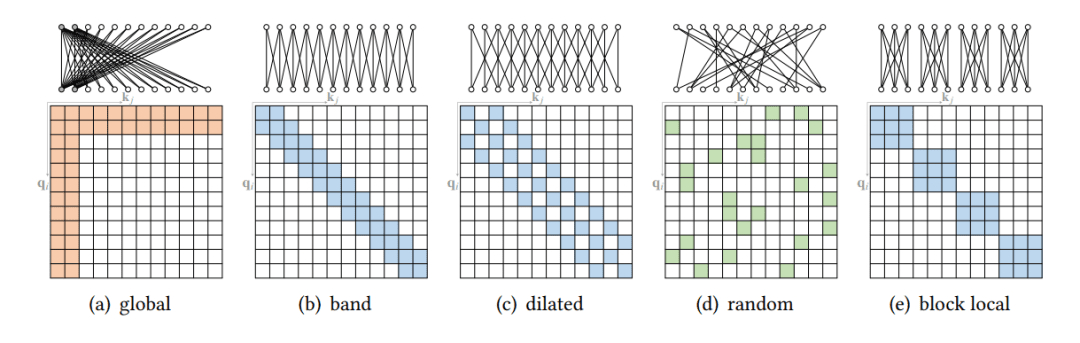
稀疏注意力机制的核心思想是在自注意力计算中引入稀疏性,即不是让序列中的每个位置都与其他所有位置进行注意力计算,而是仅选择部分位置进行计算。这种选择可以基于不同的策略,例如固定的模式(如局部窗口)、基于内容的选择(如与当前位置最相关的其他位置),或者是通过学习得到的模式。通过这种方式,稀疏注意力机制减少了计算量和内存占用,使得模型能够更高效地处理长序列。
二、方案与技术
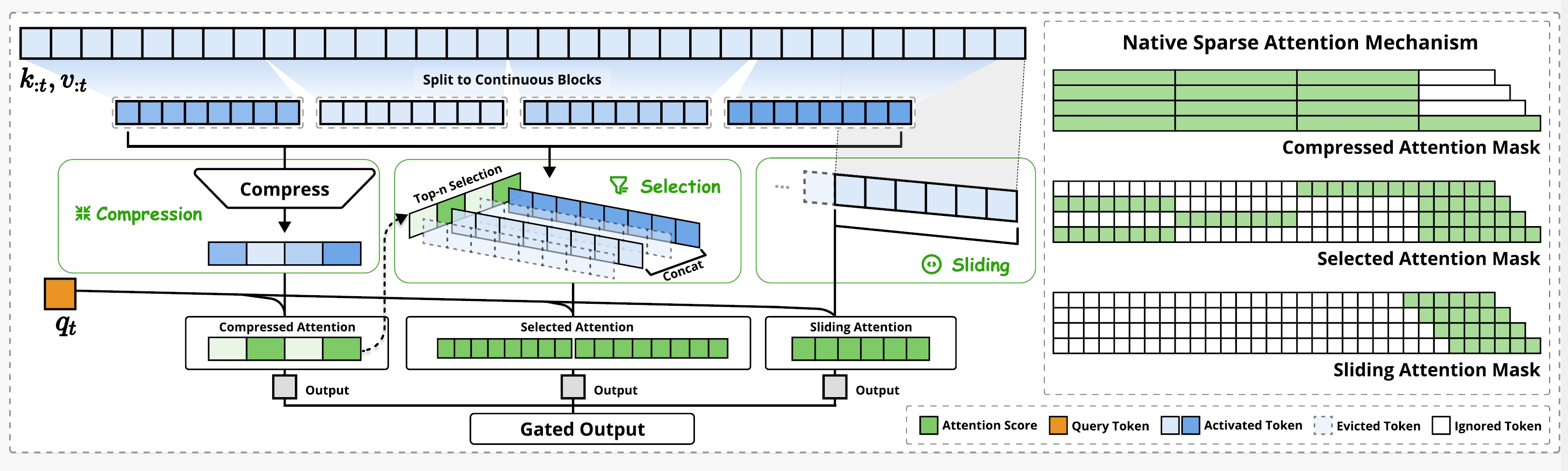
如图所示,NSA 通过将键(keys)和值(values)组织成时间块,并通过三个注意力路径处理它们来减少每个查询的计算量:压缩的粗粒度token、选择性保留的细粒度token,以及用于局部上下文信息的滑动窗口。
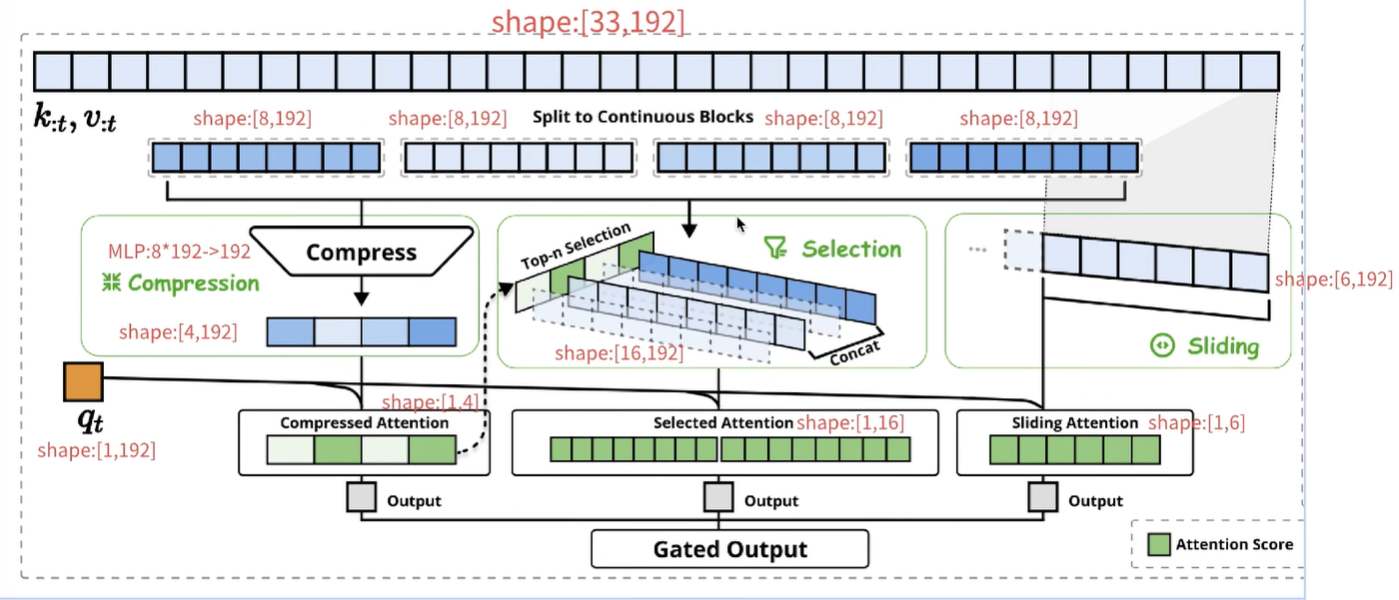
NSA改进的attention机制思路如下:
假设一段文本有33个token,假设每个token的embedding=192,那么33个token就是33 * 192;NSA处理的方式如下:
Compress/block wise selection:类似人的阅读,先看目录、提取摘要,找到重要和感兴趣的信息;这里先把token分块,上图是8个token分成一块,所以分了4块,此时就是4 * 8 * 192;最后一个是当前token,这里暂时不处理;为了达到compress的目的,8 * 192通过MLP压缩到192,所以4 * 8 * 192 → 4 * 192,核心是把上文token的K按照每8个一组,压缩成192维;K = 4 * 192,q = 192,q * K = 1 * 4了。这步的核心目的:计算当前token(这里是第33个token)和前面分组后block的距离/相似度,这步的本质是粗步找到相似度高的token范围,相当于人的粗读、看目录和摘要。
Top-n selection:这个例子中,一共4个block,当前token(第33个)与其中两个block的相似度高(图中用绿色表示),那么就把这两个绿色block内部的token拿出来,得到16 * 192、也就是16个token的K向量!继续和当前token的q向量做乘法,得到1 * 16的向量,本质就是当前token和前面所有相似度高的token计算weight,相当于人精读重要内容。
为了防止漏掉重要信息,当前token还要和前面上文token挨个做attention,这里选择的窗口还是7个token,所以当前token还要和前面紧挨着的6个token做attention;
前面三步做完后,每个步骤都能得到attention score,也就是weight权重值,当前token会利用这些weight更新自己的value,得到embedding。这些embedding向量还要经过gated输出;gate会按照一定的比例保留这三部分的embedding信息。
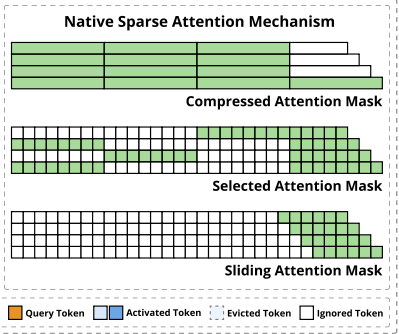
- Compressed attention mask是当前token和前面的所有block做attention,筛选相似的block;
- Selection attention
mask是和相似的block里面的token挨个做attention,比如:
- 第一行的当前token和第三个block的token做attention;
- 第二行的当前token和第一个block的token做attention;
- 第三行的当前token和第二个block的token做attention;
- sliding attention mask:和窗口内部的上文token挨个做attention
如果使用原始的attention机制,第33个token要和前面32个token做attention计算,需要计算32次;如果使用了NSA算法,整个流程4+16+6=26次attention,一个token减少(32-16)/32=19%的计算量!context越长,计算量减少地越多!
2.1 压缩注意力实现
压缩注意力的本质是将一段序列的KV压成一个KV,这样就能代表片段的全局信息。
简要描述符号压缩算子ϕ(⋅) : ℝl × d → ℝ1 × d,具体的实现可以是一个MLP层和可以学习的位置编码(内部),MLP参数与数据块长度有关。
另外关于KV序列片段的符号:
- t:序列总长度
- l:块长度
- d:为stride,目的是使得片段有重叠。当d = l时无重叠。
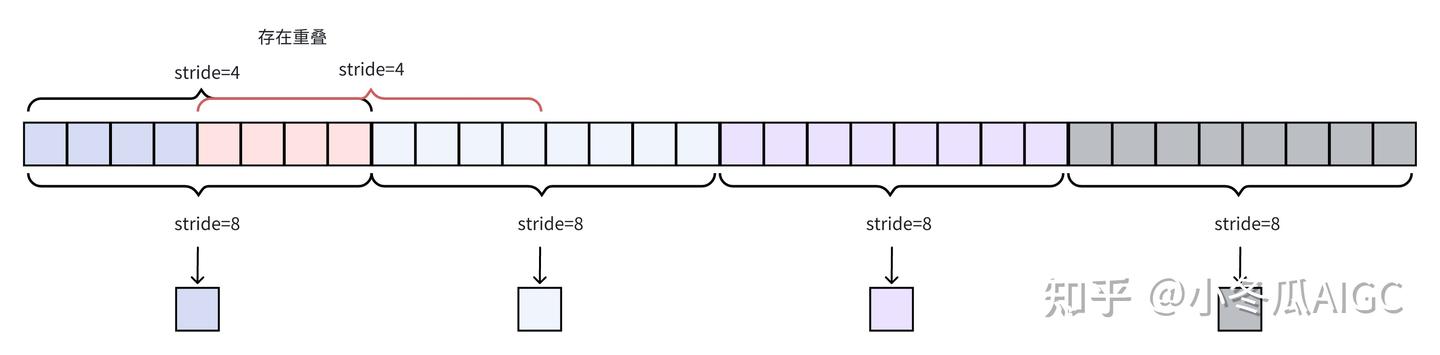
d ≠ l时
1 | |
d = l时,并且不减去l那么可见这是符合原图的KV 块划分
1 | |
压缩注意力,给定输入X ∈ ℝbs × t × dim
1 | |
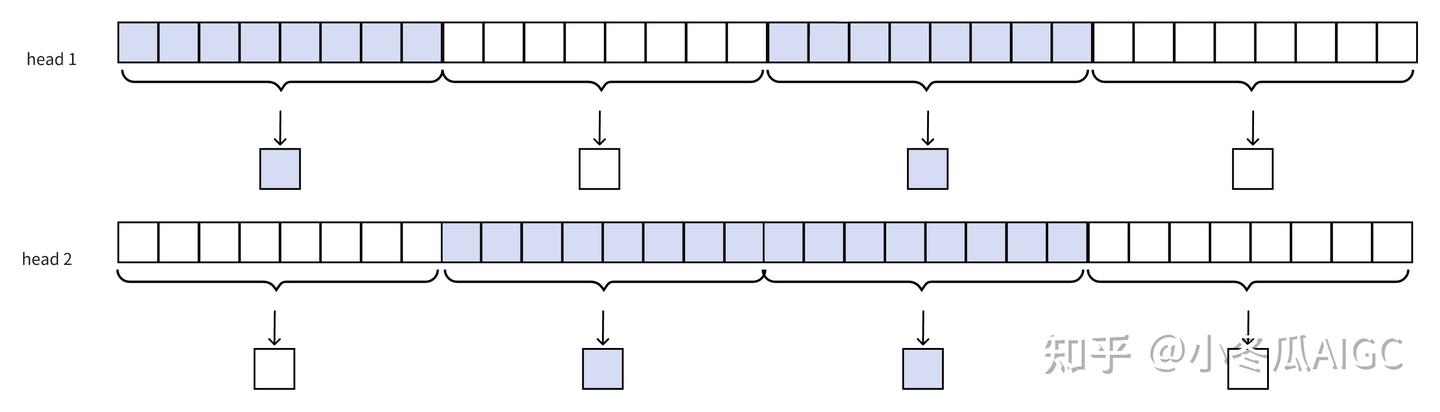
多头压缩注意力, 特别要注意:Compression Attention每个头注意到不同的片段。
1 | |
p_cmp 维度信息为:[批次大小,头数 , q序列长度 ,
压缩KV序列长度]
2.2 选择注意力实现
在压缩注意力时,q在不同头上,会注意到不同的片段,压缩注意力阶段得到了,各个头各个片段的注意力分数:
ptcmp = Softmax (qtTK̃tcmp)
以下的公式其实是按照带stride的版本写的:
代入l′ = l = d那么对于该公式,得到下式,直接与压缩注意力切分策略对应,实现就非常简单
此时可以把多头的压缩注意力分数进行聚合。这就上面提到:压缩注意力不同头,注意到不同的片段
1 | |
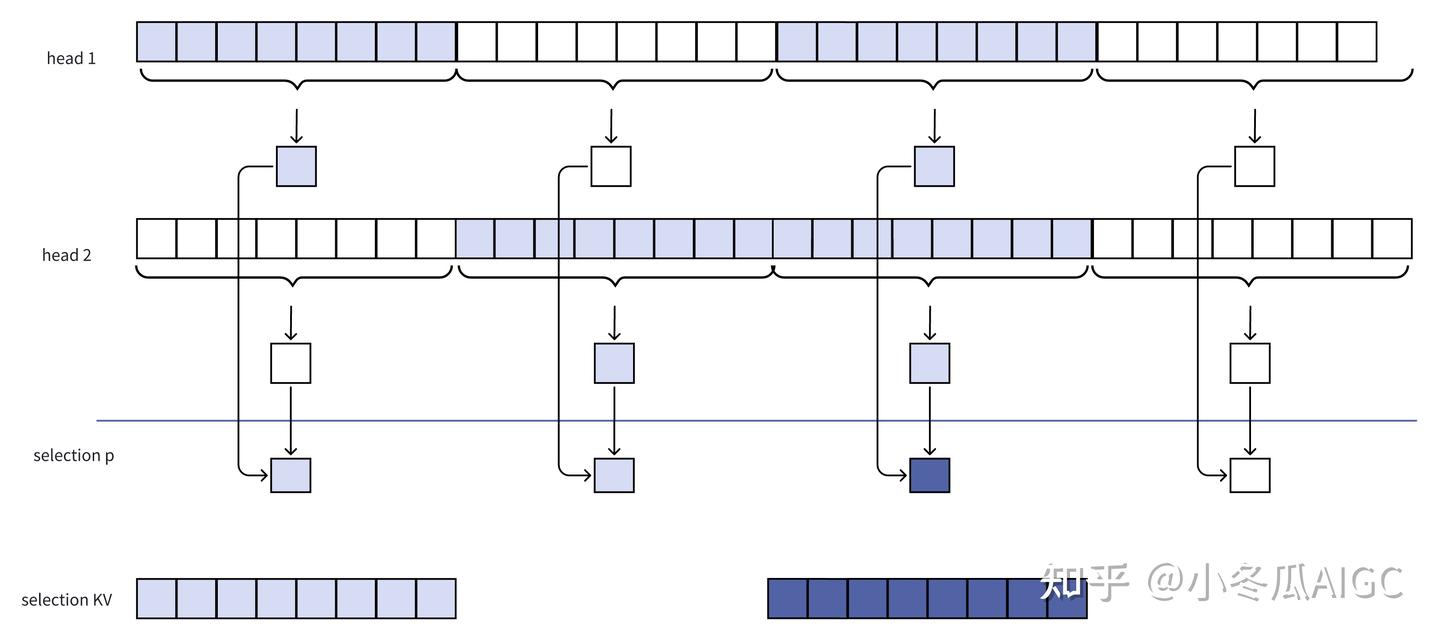
接下来进行选择, 对于不同的q有不同的注意片段维度,以下可以选取top-k出来
1 | |
提取选择到的片段对应的 KV
1 | |
上述只要选择到KV就可以计算多头注意力了。
这里的特征维度为16, 根据MQA和GQA的处理技巧,可以共享头,以此减少inference阶段的KV Cache,在“内核优化”章节里会描述这种技巧可以减少访存,图示为:
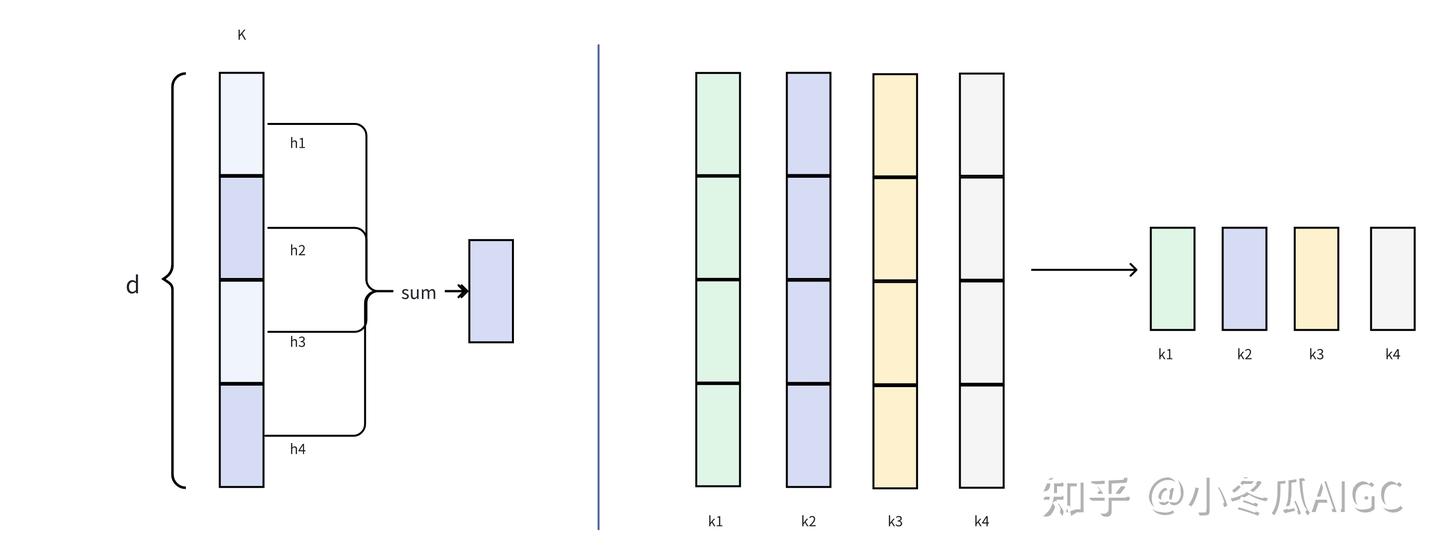
- 将dim划分成4头4维度
- 在head维度进行聚合,可以写出代码为
1 | |
可以计算选择注意力:注意每个t时刻的单个q要和多个kv计算注意力。
1 | |
选择注意力还保留一个细节,即:
- 注意力形式是GQA
- 对于一个q,有多头,那么以组的形式,不同的组选到的KV是不一样的。保证了有更多的KV信息来源。
- 而组内是单头KV,组内共享。保证计算group attention时低SRAM访存的效果。
2.3 窗口注意力实现
窗口注意力是捕捉与当前q最近的kv片段,这里做了假设,即越相近的KV就越重要,这里补全选择注意力上的“随机性”,这里的实现其实也非常简单,就是提取片段KV
K̃twin = kt − w : t, Ṽtwin = vt − w : t
代码实现为
1 | |
检验mask矩阵, 符合预期。
1 | |
快速实现一个单头的版本。
1 | |
三种注意力,他们的流程均为:
- 按照规则提取KV Cache片段。
- 对特定KV片段做特定注意力。
- 另外特定的片段长度一定原小于长文本长度,比如我们选512维片段长度,而LongContext是64000, 这悬殊的差距,将极大较少矩阵乘,我们再后需讨论如何从内核来优化 稀疏注意力,毕竟不能直接用标准矩阵乘
2.4 注意力聚合
在上述三个注意力计算中,都得到了同样维度[1, 32, 16] 的注意力输出,这里的门控实现
1 | |
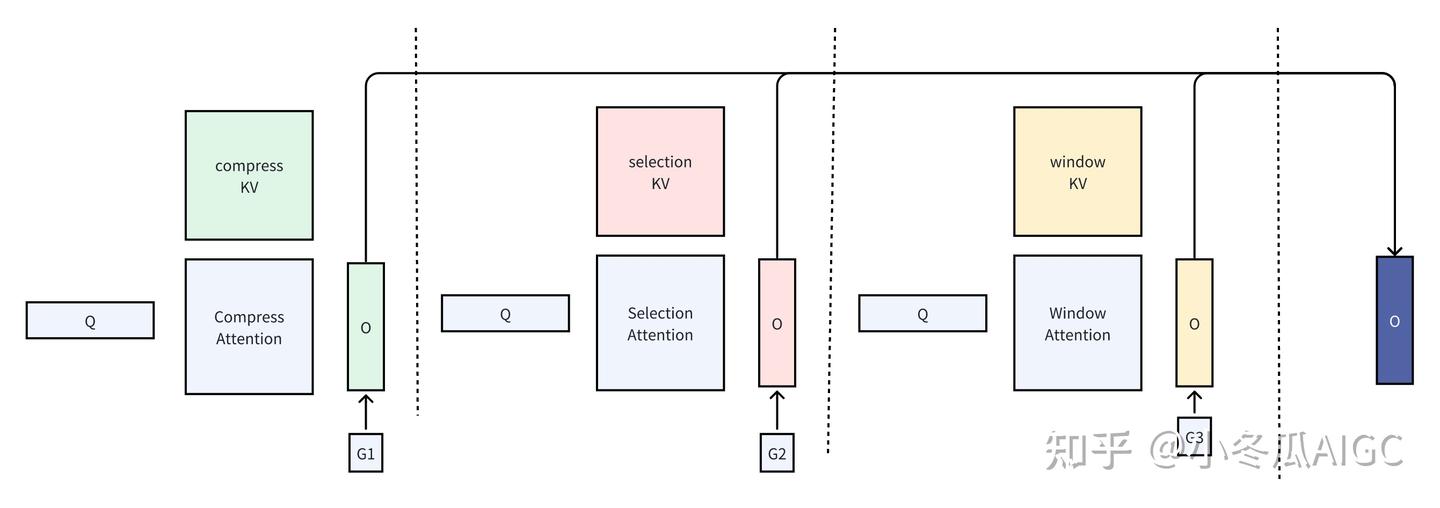
那么计算完整的NSA,𝒞代表三种注意力方法
ot* = ∑c ∈ 𝒞gtc ⋅ Attn(qt, K̃tc, Ṽtc)
1 | |
另外NSA就是再提取不同片段的KV,可以算提出的KV总量与原KV长度,就能知道减少了多少的计算量
Nt = ∑c ∈ 𝒞size[K̃tc]
如果原KV长度为t, 那么有Nt ≪ t
2.5 内核优化
DeepSeek团队重新用triton编写了NSA的注意力算子,本质上与Flash-Attention2思路没有大区别,简要描述
注意力实现:整体来看的话,NSA实质的Attention计算是GQA,以一组注意力来说,涉及到多头Q和单头KV:
- 常规:需要将单头KV,复制成与Q头数相对应的KV,送到SRAM计算注意力
- NSA:单头KV送到SRAM,这里不需要复制多头。
内核实现:
Grid Loop:先加载单个多头Q,逐个元素来算NSA,注意看维度有dk × h,h为头数量
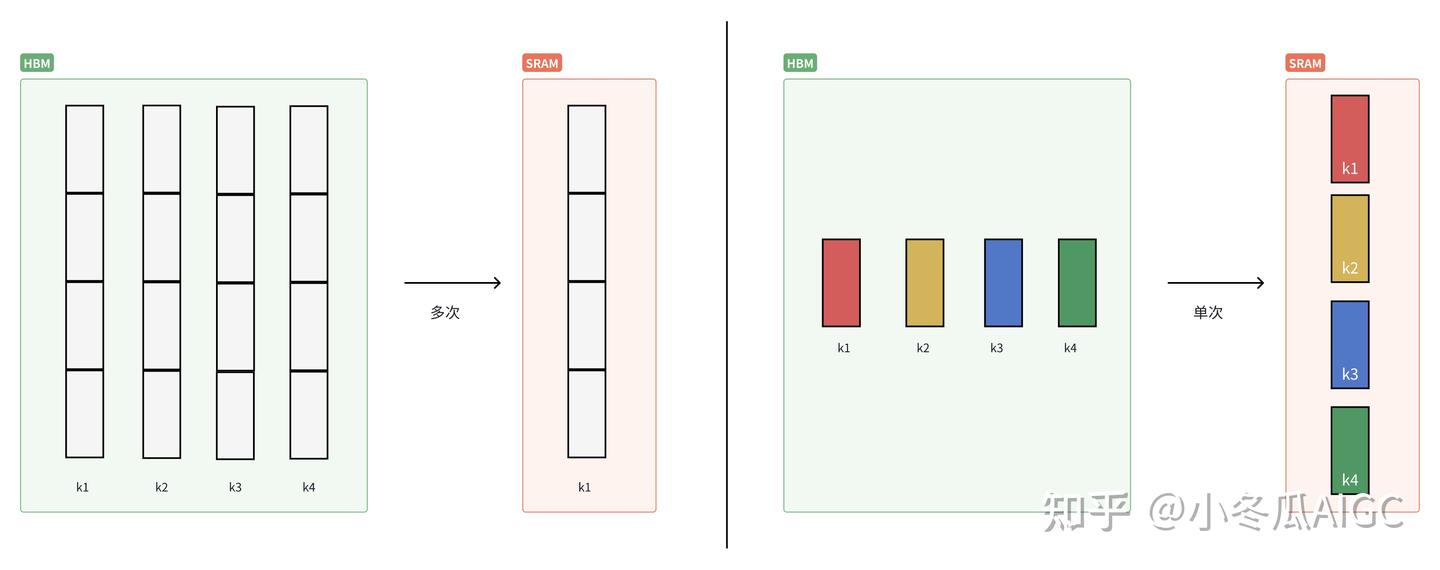
Inner Loop:单头K,载入维度为dk × Bk,Bk为一个片段,这里并没有头维度,所以从始至终在一个Group里,在HBM/SRAM都是单头KV而存在的。对于一个GQA里的一个Group来说,需要将单头KV复制成多头KV,这里内核优化的关键在于,通过单头按照某种共享内存策略,让多头(multi-grid) 都能访问到一个share的KV,这样就不用复制KV成多头了。
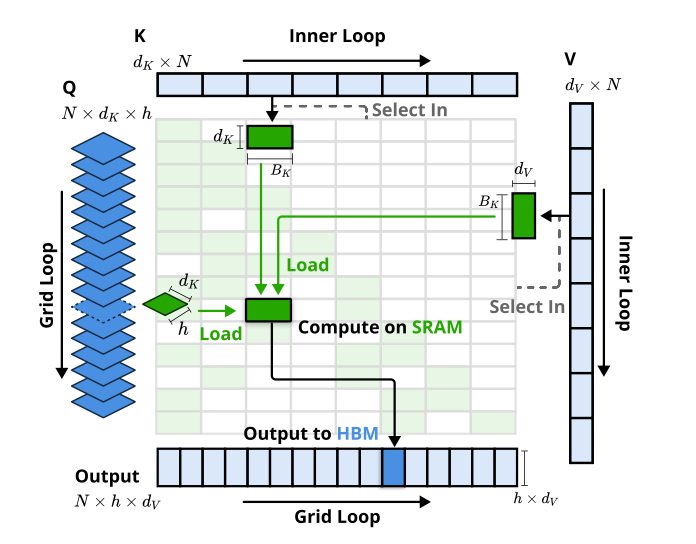
以上的一个绿色块代表了一个q和一段kv计算。这里,当t增大时,由于KV块恒为3块,那么越长NSA的加速越明显。
Selection Attention才是真正体现了Sparse的精髓。下图的注意力计算发生在Selection Attention中,以GQA/MQA视角来看, 一个组内只需要单头KV; 从SRAM视角来看:单头KV可以减少HBM与SRAM的访存量。
三、NSA分析
3.1 稀疏化注意力机制分析
- 标准的attention(MHA) 有一定的稀疏性,稀疏性的学习是自动的,但是MHA并没有对极小的注意力分数进行过滤
NSA其实可以看成是分层的注意力学习机制,我们以选择注意力来说:压缩注意力是外层稀疏性建模,选择注意力是内层注意力建模。这里的稀疏性是发生在外层,好处在于只计算几个极小量的(K, V)(cmp)的注意力就能筛选出局部的精细KV出来。
另外要分析稀疏化化的影响,稀疏化如果作用在文本序列上来说是信息是割裂的,这个影响在NSA的机制是否严重,考虑单层和多层注意力的NSA
QKV信息量。
- 单层:非选择到的KV块被丢弃
- 层:
下例所示有4个数据块,第一层
NSA选取到1,3片段,第二层NSA选取到2,3 片段, 第三层NSA选取到1,4片段,那么可以了解到,经过多层处理这里的数据切割的影响是会被减轻的。
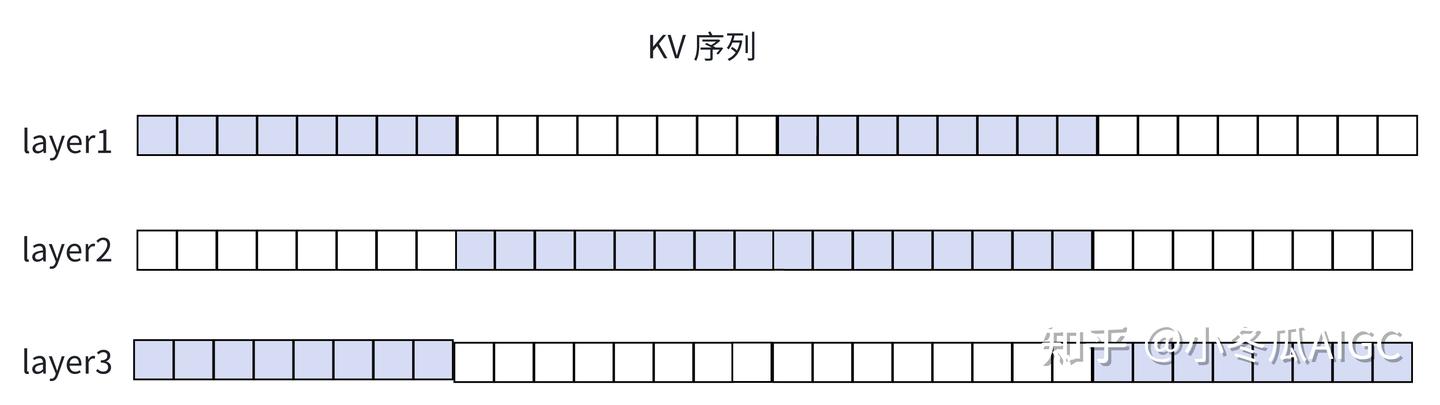
当前的q信息会流转到下一层的KV上,那么就意味着选择哪一个数据块,实际上都有完整的历史的前驱Q信息。即在第一层attention以后,所有流向的特征都已经经过序列建模的。
3.2 NSA Inference analysis
在NSA在inference过程中,在计算NSA之前,KV-Cache存储实际上是不会减少的。
再分析三种注意力是否能内部加入mini-kv-cache
在prefill阶段:
- 压缩注意力:做标准的注意力forward
- 选择注意力:做block-wise的注意力,由于稀疏性原因,可以大幅减轻首token计算时间的原因
- 窗口注意力:做标准的注意力forward
在decoding阶段:
在计算层面,实际上计算量是固定的为单个q 和 固定数量的 KV 进行注意力, 标准的注意力KV是随context累增的。
- 压缩注意力:由于kv是累增的,那么Kcmp是累增的,可以加入mini-kv-cache
- 选择注意力:复用原KV-Cache
- 窗口注意力:复用原KV-Cache