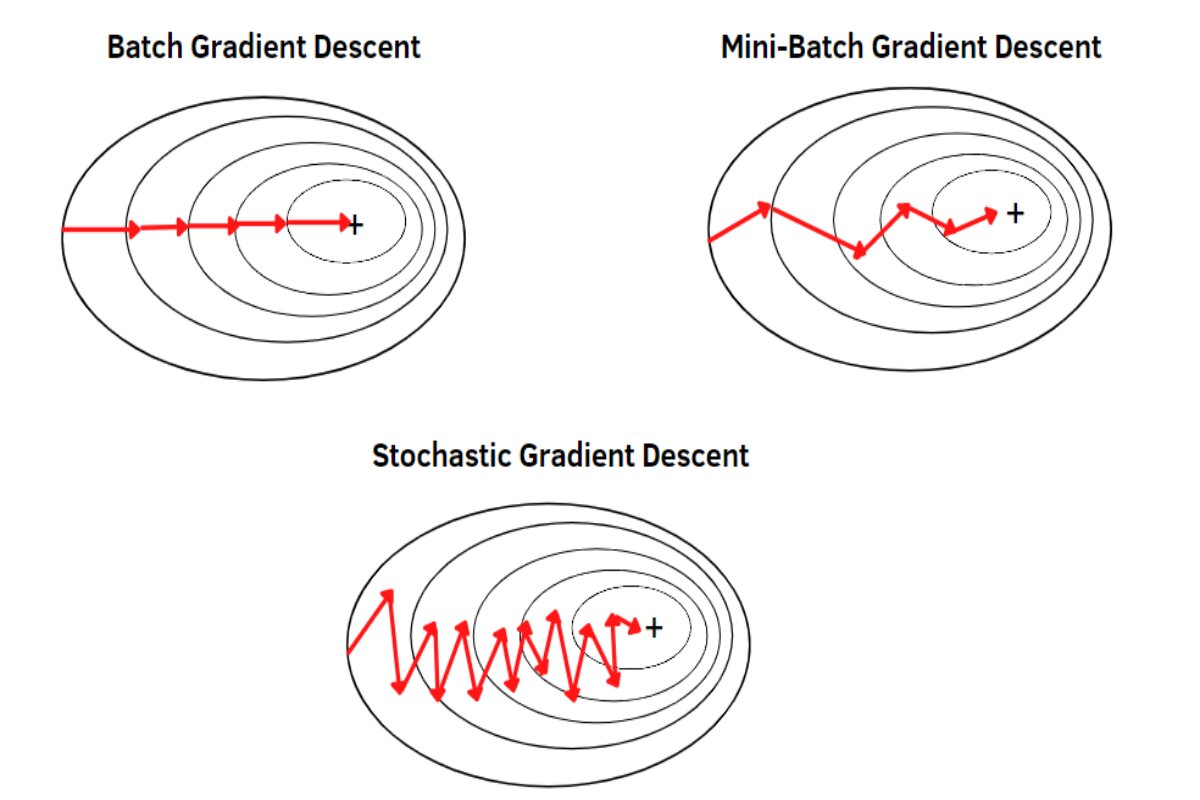
优化算法在神经网络训练中至关重要,它们决定了如何调整模型参数以最小化损失函数。以下是对神经网络中常用优化算法的详细总结,包括梯度下降及其变种。
一、梯度下降(Gradient
Descent)
梯度下降是最基础的优化算法,通过沿着损失函数梯度的反方向更新参数,逐步减少损失。
算法步骤
初始化参数 :随机初始化参数 θ 计算梯度 :计算损失函数 J (θ )θ ∇θ J (θ ) 。更新参数 :沿梯度反方向更新参数: θ = θ − η ∇θ J (θ )η
1.1 一维梯度下降
连续可微实值函数f : ℝ → ℝ
f (x + ϵ ) = f (x ) + ϵ f ′ (x ) + 𝒪(ϵ 2 ).
即在一阶近似中,f (x + ϵ )x f (x )f ′ (x )ϵ f η > 0ϵ = −η f ′ (x )
f (x − η f ′ (x )) = f (x ) − η f ′ 2 (x ) + 𝒪(η 2 f ′ 2 (x )).
如果其导数f ′ (x ) ≠ 0η f ′ 2 (x ) > 0η
f (x − η f ′ (x )) ⪅ f (x ).
这意味着,如果使用
x ← x − η f ′ (x )
来迭代x f (x )x η > 0x |f ′ (x )| 的幅度足够小或迭代次数达到某个值时。
下面展示如何实现梯度下降。为了简单起见,选用目标函数f (x ) = x 2 x
绘图
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 %matplotlib inlineimport numpy as npfrom torch.utils import dataimport torchimport pandas as pdimport mathimport hashlibimport osimport tarfileimport zipfileimport requestsfrom IPython import displayimport timefrom mpl_toolkits import mplot3dfrom matplotlib import pyplot as pltfrom matplotlib_inline import backend_inlinedef set_figsize (figsize=(3.5 , 2.5 ): """设置matplotlib的图表大小""" 'svg' )'figure.figsize' ] = figsizedef set_axes (axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend ):"""设置matplotlib的轴""" if legend:def plot (X, Y=None , xlabel=None , ylabel=None , legend=None , xlim=None , ylim=None , xscale='linear' , yscale='linear' , fmts=('-' , 'm--' , 'g-.' , 'r:' 3.5 , 2.5 None ):"""绘制数据点""" if legend is None :if axes else plt.gca()def has_one_axis (X ):return (hasattr (X, "ndim" ) and X.ndim == 1 or isinstance (X, list )and not hasattr (X[0 ], "__len__" ))if has_one_axis(X):if Y is None :len (X), Xelif has_one_axis(Y):if len (X) != len (Y):len (Y)for x, y, fmt in zip (X, Y, fmts):if len (x):else :def show_trace (results, f ):max (abs (min (results)), abs (max (results)))0.01 )for x in f_line], [for x in results]], 'x' , 'f(x)' , fmts=['-' , '-o' ])def show_trace_2d (f, results ): """显示优化过程中2D变量的轨迹""" zip (*results), '-o' , color='#ff7f0e' )5.5 , 1.0 , 0.1 ),3.0 , 1.0 , 0.1 ))'#1f77b4' )'x1' )'x2' )class Animator : """在动画中绘制数据""" def __init__ (self, xlabel=None , ylabel=None , legend=None , xlim=None , ylim=None , xscale='linear' , yscale='linear' , fmts=('-' , 'm--' , 'g-.' , 'r:' 1 , ncols=1 , figsize=(3.5 , 2.5 ):if legend is None :'svg' )self .fig, self .axes = plt.subplots(nrows, ncols, figsize=figsize)if nrows * ncols == 1 :self .axes = [self .axes, ]self .config_axes = lambda : set_axes(self .axes[0 ], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)self .X, self .Y, self .fmts = None , None , fmtsdef add (self, x, y ):if not hasattr (y, "__len__" ):len (y)if not hasattr (x, "__len__" ):if not self .X:self .X = [[] for _ in range (n)]if not self .Y:self .Y = [[] for _ in range (n)]for i, (a, b) in enumerate (zip (x, y)):if a is not None and b is not None :self .X[i].append(a)self .Y[i].append(b)self .axes[0 ].cla()for x, y, fmt in zip (self .X, self .Y, self .fmts):self .axes[0 ].plot(x, y, fmt)self .config_axes()self .fig)True )
训练函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 def train_2d (trainer, steps=20 , f_grad=None ): """用定制的训练机优化2D目标函数""" 5 , -2 , 0 , 0 for i in range (steps):if f_grad:import hashlibelse :print (f'epoch {i + 1 } , x1: {float (x1):f} , x2: {float (x2):f} ' )return resultsdef train11 (trainer_fn, states, hyperparams, data_iter, feature_dim, num_epochs=2 ):0.0 , std=0.01 , size=(feature_dim, 1 ),True )1 ), requires_grad=True )lambda X: linreg(X, w, b), squared_loss'epoch' , ylabel='loss' ,0 , num_epochs], ylim=[0.22 , 0.35 ])0 , Timer()for _ in range (num_epochs):for X, y in data_iter:0 ]if n % 200 == 0 :0 ]/len (data_iter),print (f'loss: {animator.Y[0 ][-1 ]:.3 f} , {timer.avg():.3 f} sec/epoch' )return timer.cumsum(), animator.Y[0 ]
用时统计
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Timer : """记录多次运行时间""" def __init__ (self ):self .times = []self .start()def start (self ):"""启动计时器""" self .tik = time.time()def stop (self ):"""停止计时器并将时间记录在列表中""" self .times.append(time.time() - self .tik)return self .times[-1 ]def avg (self ):"""返回平均时间""" return sum (self .times) / len (self .times)def sum (self ):"""返回时间总和""" return sum (self .times)def cumsum (self ):"""返回累计时间""" return np.array(self .times).cumsum().tolist()
评估函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 def linreg (X, w, b ): """线性回归模型""" return torch.matmul(X, w) + bdef squared_loss (y_hat, y ): """均方损失""" return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2 def accuracy (y_hat, y ):"""计算预测正确的数量""" if len (y_hat.shape) > 1 and y_hat.shape[1 ] > 1 :1 )type (y.dtype) == yreturn float (cmp.type (y.dtype).sum ())def evaluate_loss (net, data_iter, loss ): """评估给定数据集上模型的损失""" 2 ) for X, y in data_iter:sum (), l.numel())return metric[0 ] / metric[1 ]def evaluate_accuracy (net, data_iter ): """计算在指定数据集上模型的精度""" if isinstance (net, torch.nn.Module):eval () 2 ) with torch.no_grad():for X, y in data_iter:return metric[0 ] / metric[1 ]class Accumulator : """在n个变量上累加""" def __init__ (self, n ):self .data = [0.0 ] * ndef add (self, *args ):self .data = [a + float (b) for a, b in zip (self .data, args)]def reset (self ):self .data = [0.0 ] * len (self .data)def __getitem__ (self, idx ):return self .data[idx]
数据加载
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 DATA_HUB = dict ()'http://d2l-data.s3-accelerate.amazonaws.com/' def load_array (data_arrays, batch_size, is_train=True ): """构造一个PyTorch数据迭代器""" return data.DataLoader(dataset, batch_size, shuffle=is_train)def download (name, cache_dir=os.path.join('..' , 'data' ): """下载一个DATA_HUB中的文件,返回本地文件名""" assert name in DATA_HUB, f"{name} 不存在于 {DATA_HUB} " True )'/' )[-1 ])if os.path.exists(fname):with open (fname, 'rb' ) as f:while True :1048576 )if not data:break if sha1.hexdigest() == sha1_hash:return fname print (f'正在从{url} 下载{fname} ...' )True , verify=True )with open (fname, 'wb' ) as f:return fnamedef download_extract (name, folder=None ): """下载并解压zip/tar文件""" if ext == '.zip' :'r' )elif ext in ('.tar' , '.gz' ):open (fname, 'r' )else :assert False , '只有zip/tar文件可以被解压缩' return os.path.join(base_dir, folder) if folder else data_dirdef download_all (): """下载DATA_HUB中的所有文件""" for name in DATA_HUB:'airfoil' ] = (DATA_URL + 'airfoil_self_noise.dat' ,'76e5be1548fd8222e5074cf0faae75edff8cf93f' )def get_data (batch_size=10 , n=1500 ):'airfoil' ),'\t' )0 )) / data.std(axis=0 ))1 ], data[:n, -1 ]),True )return data_iter, data.shape[1 ]-1
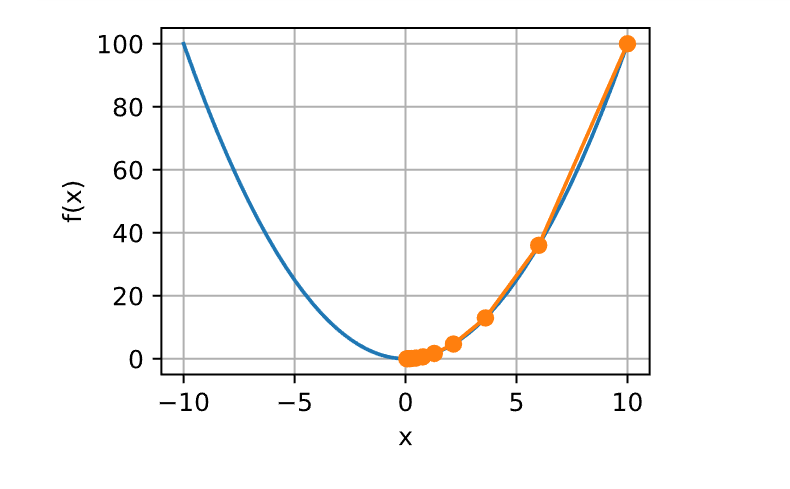
使用x = 10η = 0.2x x
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 def f (x ): return x ** 2 def f_grad (x ): return 2 * xdef gd (eta, f_grad ):10.0 for i in range (10 ):float (x))print (f'epoch 10, x: {x:f} ' )return results0.2 , f_grad)
1.1.1 学习率
学习率 (learning
rate)决定目标函数能否收敛到局部最小值,以及何时收敛到最小值。学习率η x η = 0.05
1 show_trace(gd(0.05 , f_grad), f)
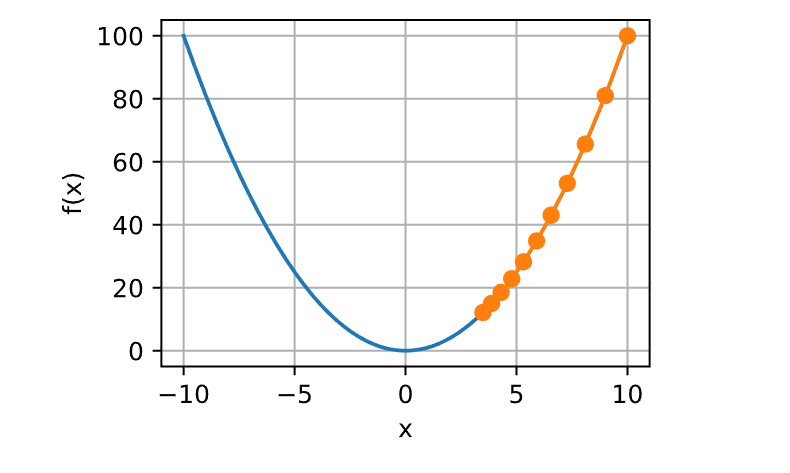
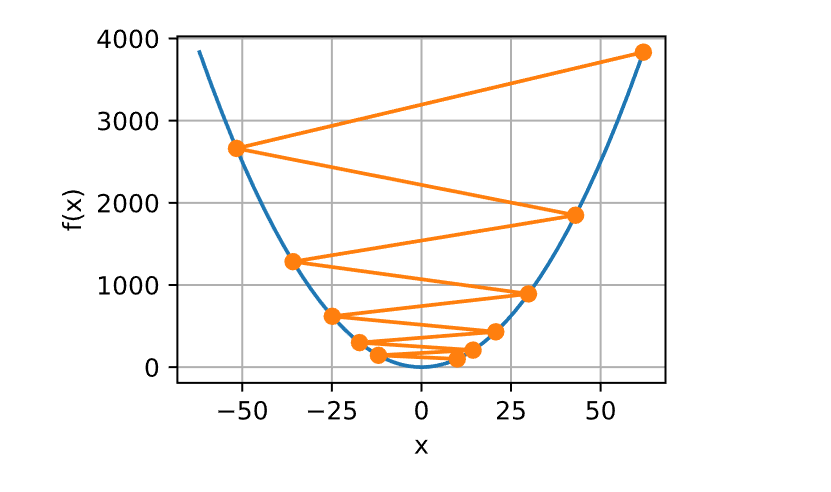
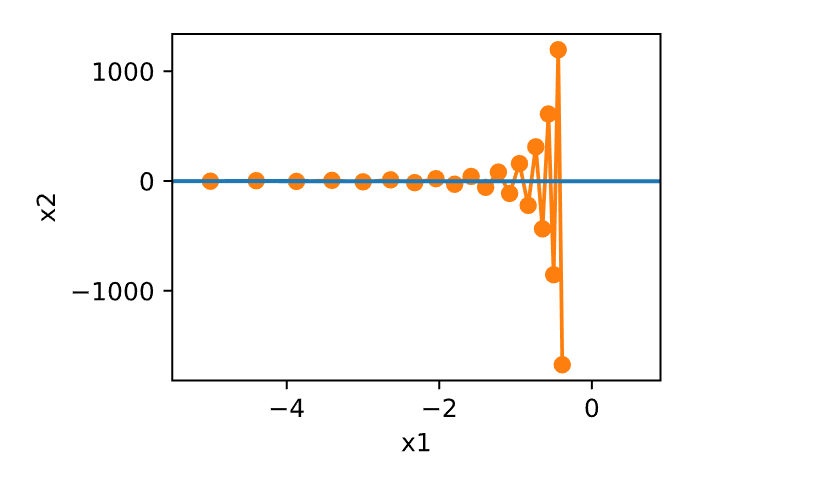
如果使用过高的学习率,x f (x )η = 1.1x x = 0
1 show_trace(gd(1.1 , f_grad), f)
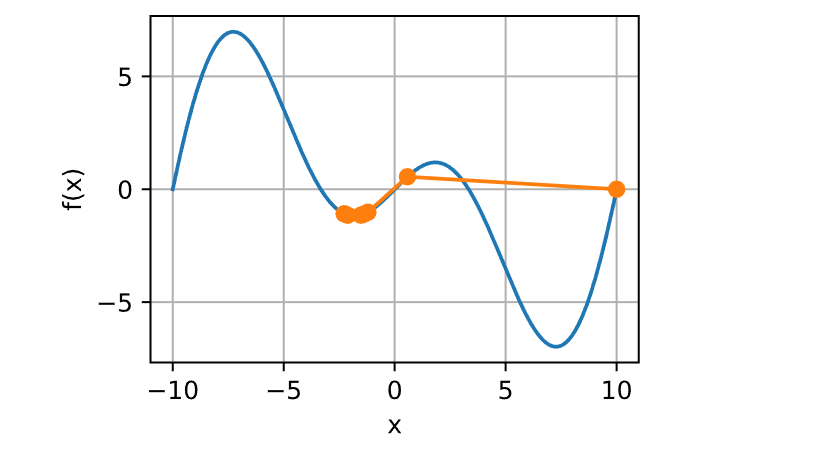
1.1.2 局部最小值
对于非凸函数的梯度下降,如函数f (x ) = x ⋅ cos (c x )c
1 2 3 4 5 6 7 8 9 c = torch.tensor(0.15 * np.pi)def f (x ): return x * torch.cos(c * x)def f_grad (x ): return torch.cos(c * x) - c * x * torch.sin(c * x)2 , f_grad), f)
1.2 多元梯度下降
对于多元x = [x 1 , x 2 , …, x d ⊤ f : ℝd d
梯度中的每个偏导数元素∂f (x )/∂x i 代表了当输入x i f x
f (x + ϵ ) = f (x ) + ϵ ⊤ ∇f (x ) + 𝒪(∥ϵ ∥2 ).
在ϵ −∇f (x ) 得出。选择合适的学习率η > 0
x ← x − η ∇f (x ).
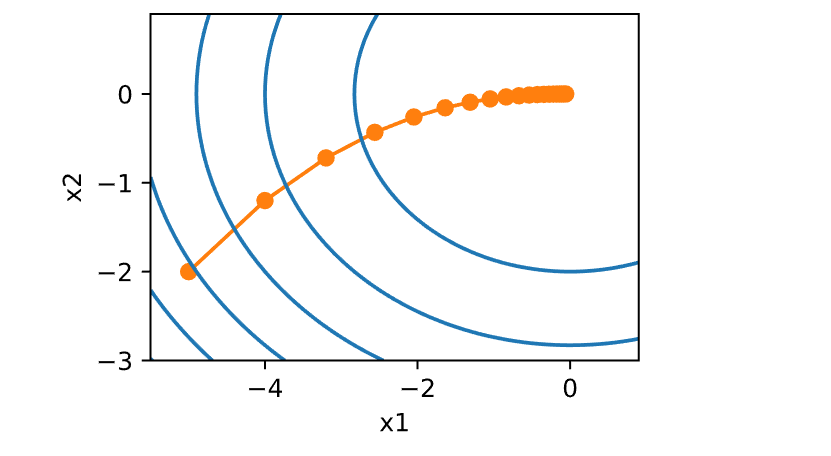
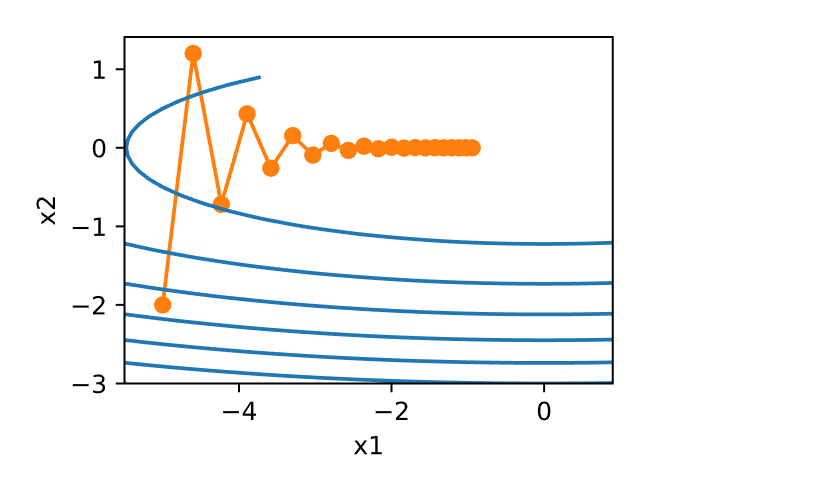
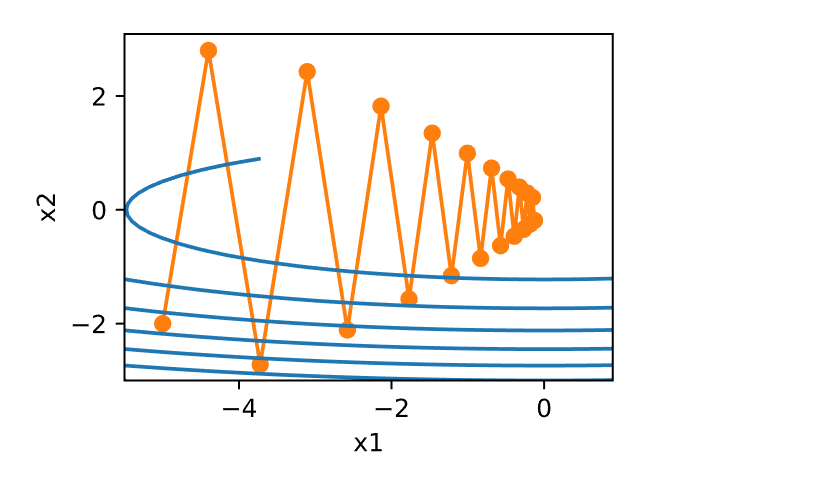
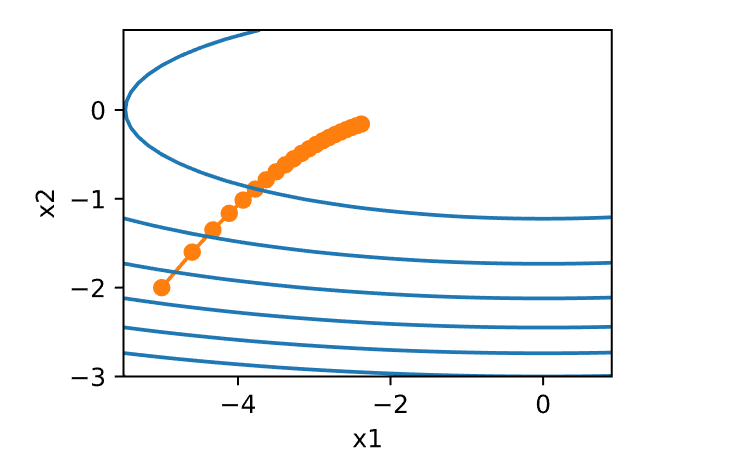
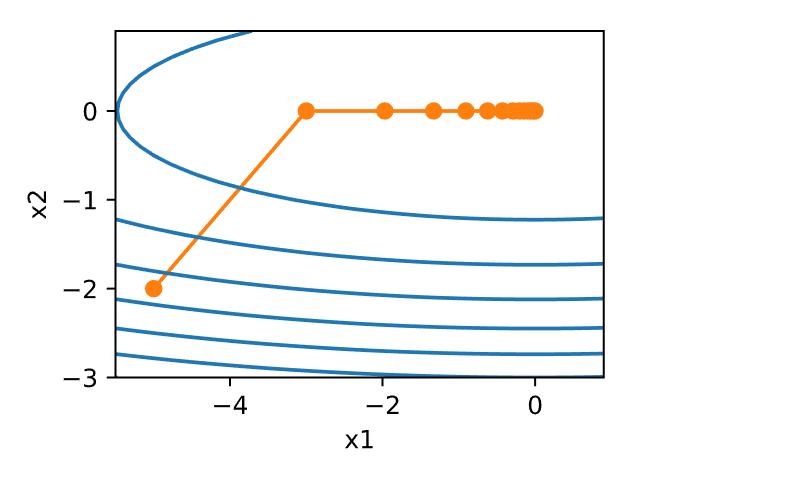
构造一个目标函数f (x ) = x 1 2 + 2x 2 2 x = [x 1 , x 2 ]⊤ ∇f (x ) = [2x 1 , 4x 2 ]⊤ 给出。从初始位置[−5, −2] 通过梯度下降观察x
观察学习率η = 0.1x x [0, 0] 的最小值。虽然进展相当顺利,但相当缓慢。
1 2 3 4 5 6 7 8 9 10 11 12 def f_2d (x1, x2 ): return x1 ** 2 + 2 * x2 ** 2 def f_2d_grad (x1, x2 ): return (2 * x1, 4 * x2)def gd_2d (x1, x2, s1, s2, f_grad ):return (x1 - eta * g1, x2 - eta * g2, 0 , 0 )0.1
1 epoch 20, x1: -0.057646, x2: -0.000073
学习率的大小很重要:学习率太大会使模型发散,学习率太小会没有进展。
梯度下降会可能陷入局部极小值,而得不到全局最小值。
类型
批量梯度下降(Batch Gradient
Descent) :在整个训练集上计算梯度。收敛稳定,但计算开销大。随机梯度下降(Stochastic Gradient
Descent,SGD) :在每个样本上计算梯度。每次更新快,但可能产生高波动。小批量梯度下降(Mini-Batch Gradient
Descent) :在小批量样本上计算梯度。平衡了批量和随机梯度下降的优点。
二、随机梯度下降(Stochastic
Gradient Descent,SGD)
在深度学习中,目标函数通常是训练数据集中每个样本的损失函数的平均值。给定n f i x )i x
x
如果使用梯度下降法,则每个自变量迭代的计算代价为𝒪(n ) ,它随n
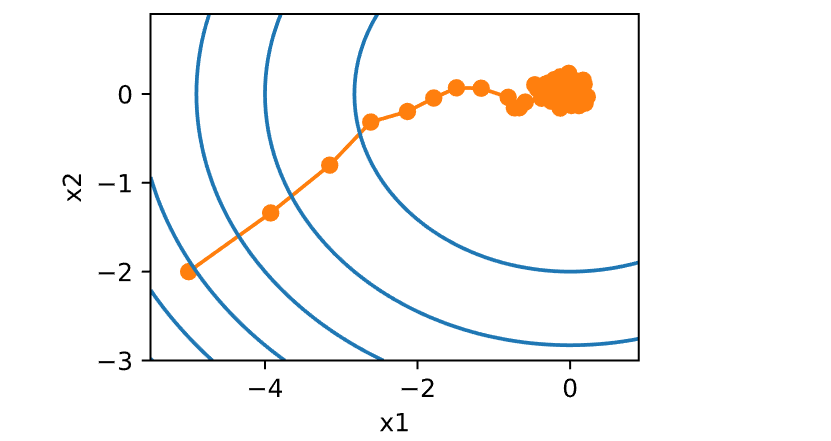
2.1 随机梯度更新
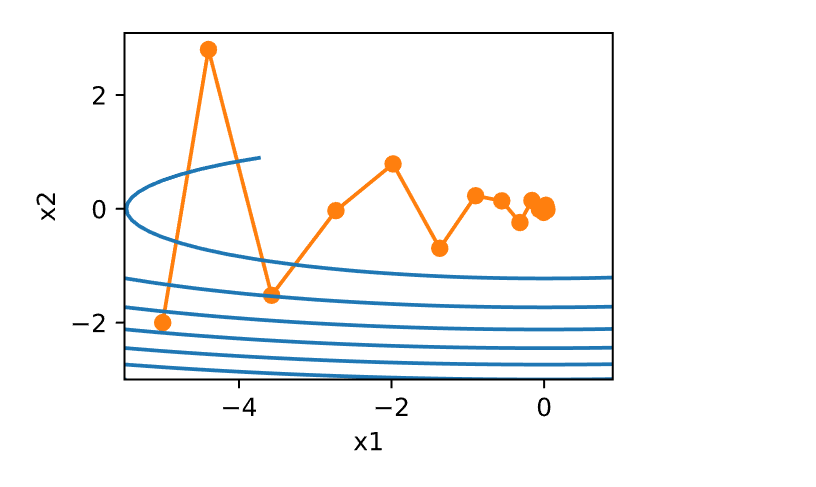
随机梯度下降(SGD)可降低每次迭代时的计算代价。在随机梯度下降的每次迭代中,对数据样本随机均匀采样一个索引i i ∈ {1, …, n }∇f i x ) 以更新x
x ← x − η ∇f i x ),
其中η 𝒪(n ) 降至常数𝒪(1) 。随机梯度∇f i x ) 是对完整梯度∇f (x ) 的无偏估计,因为
这意味着,平均而言,随机梯度是对梯度的良好估计。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 def f (x1, x2 ): return x1 ** 2 + 2 * x2 ** 2 def f_grad (x1, x2 ): return 2 * x1, 4 * x2def sgd (x1, x2, s1, s2, f_grad ):0.0 , 1 , (1 ,)).item()0.0 , 1 , (1 ,)).item()return (x1 - eta_t * g1, x2 - eta_t * g2, 0 , 0 )def constant_lr ():return 1 0.1 50 , f_grad=f_grad))
1 epoch 50, x1: -0.207942, x2: 0.160768
2.2 动态学习率
用与时间相关的学习率η (t )η η η
分 段 常 数 指 数 衰 减 多 项 式 衰 减
在第一个分段常数 (piecewise
constant)场景中,会降低学习率,例如,每当优化进度停顿时。这是训练深度网络的常见策略。或者,可以通过指数衰减 (exponential
decay)来更积极地减低它。不幸的是,这往往会导致算法收敛之前过早停止。一个受欢迎的选择是α = 0.5多项式衰减 (polynomial
decay)。
指数衰减
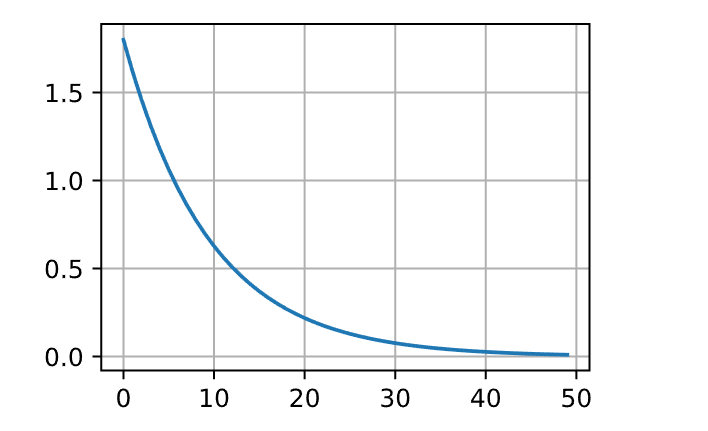
1 2 3 4 5 6 7 8 9 def exponential_lr ():global t1 return math.exp(-0.1 * t)1 1000 , f_grad=f_grad))
1 epoch 1000, x1: -0.795551, x2: -0.042453
即使经过1000个迭代步骤,仍然离最优解很远。事实上,该算法根本无法收敛。另一方面,如果使用多项式衰减,其中学习率随迭代次数的平方根倒数衰减,那么仅在50次迭代之后,收敛就会更好。
1 2 3 4 5 6 7 8 9 def polynomial_lr ():global t1 return (1 + 0.1 * t) ** (-0.5 )1 50 , f_grad=f_grad))
1 epoch 50, x1: -0.191217, x2: -0.026836
三、小批量梯度下降(Mini-Batch
Gradient Descent)
GD中使用完整数据集来计算梯度并更新参数,SGD中一次处理一个训练样本来取得进展。
小批量梯度下降在每次更新时用b个样本,批量的梯度下降是一种折中的方法。
处理单个观测值需要执行许多单一矩阵-矢量(甚至矢量-矢量)乘法,这耗费相当大,而且对应深度学习框架也要巨大的开销。这既适用于计算梯度以更新参数时,也适用于用神经网络预测。也就是说,每当执行w ← w − η t g t
g t w f (x t w ).
可以通过将其应用于一个小批量观测值来提高此操作的计算 效率。也就是说,将梯度g t
由于x t ℬt 的所有元素都是从训练集中随机抽出的,因此梯度的期望保持不变。
另一方面,方差显著降低。由于小批量梯度由正在被平均计算的b := |ℬt
可以通过将小批量设置为1500(即样本总数)来实现。
因此,模型参数每个迭代轮数只迭代一次。
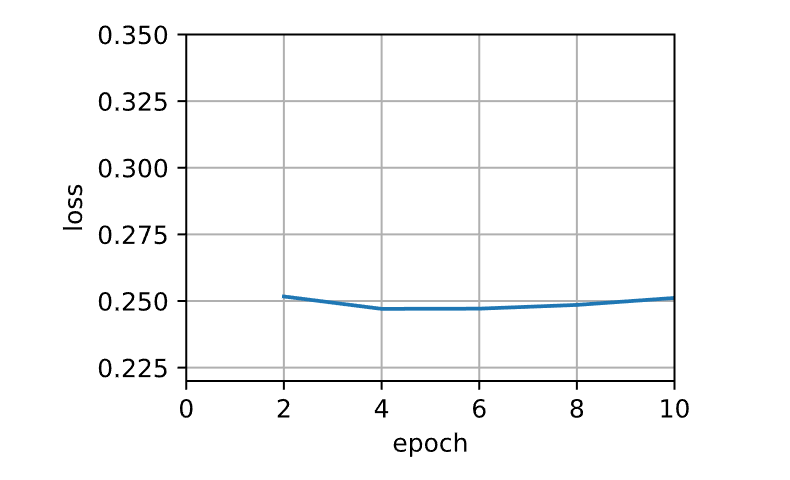
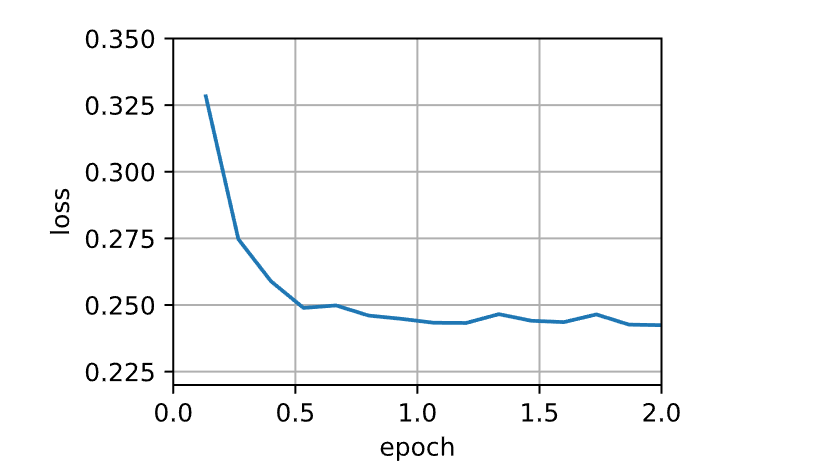
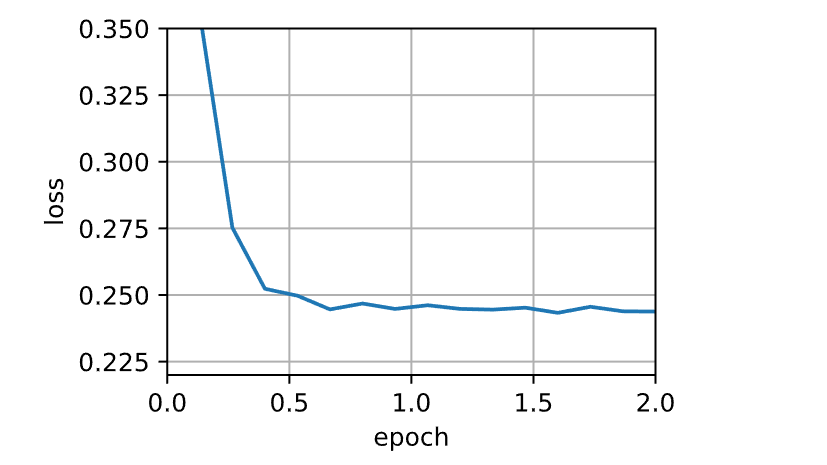
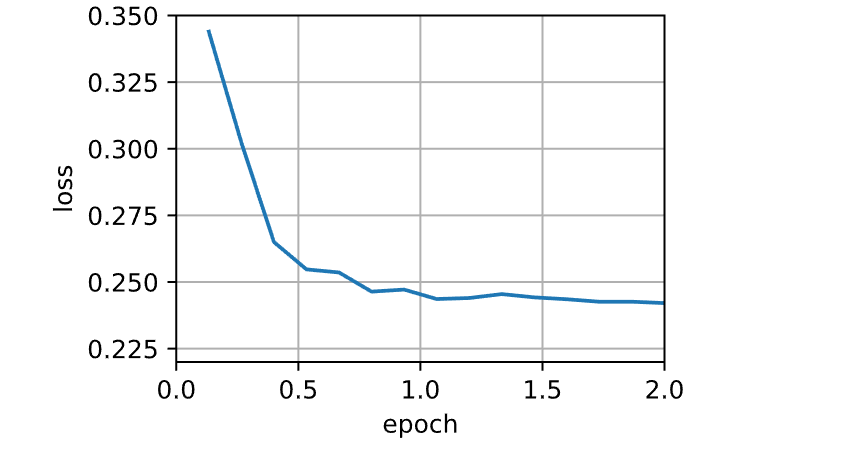
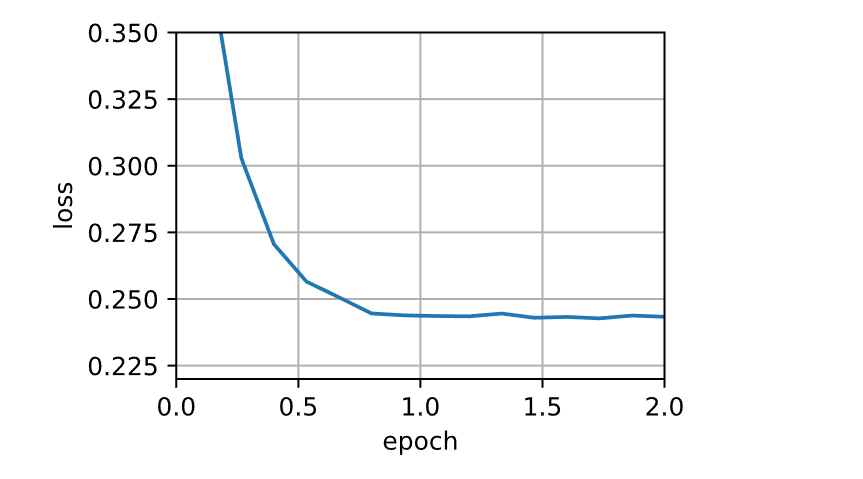
1 2 3 4 5 6 7 def train_sgd (lr, batch_size, num_epochs=2 ):return train_ch11(None , {'lr' : lr}, data_iter, feature_dim, num_epochs)1 , 1500 , 10 )
1 loss: 0.251, 0.007 sec/epoch
当批量大小为1时,优化使用的是随机梯度下降。在随机梯度下降中,每当一个样本被处理,模型参数都会更新。目标函数值的下降在1个迭代轮数后就变得较为平缓。随机梯度下降的一个迭代轮数耗时更多。这是因为随机梯度下降更频繁地更新了参数,而且一次处理单个观测值效率较低。
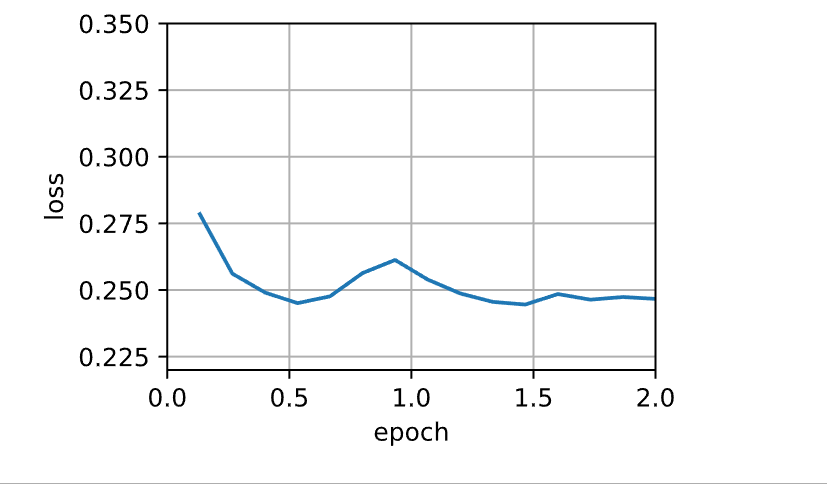
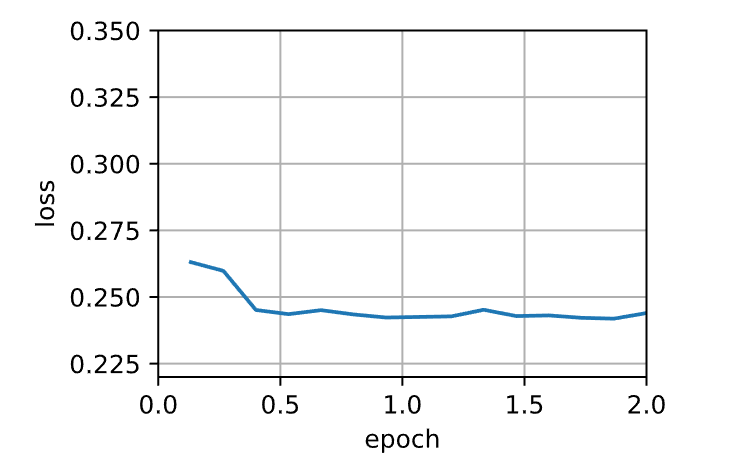
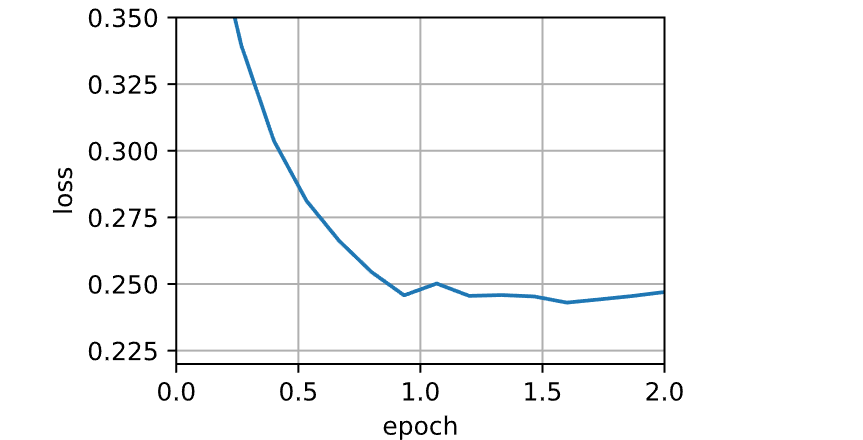
1 sgd_res = train_sgd(0.005 , 1 )
1 loss: 0.248, 0.014 sec/epoch
当批量大小等于100时,使用小批量随机梯度下降进行优化。每个迭代轮数所需的时间比随机梯度下降和批量梯度下降所需的时间短。
1 mini1_res = train_sgd(.4 , 100 )
1 loss: 0.246, 0.001 sec/epoch
将批量大小减少到10,每个迭代轮数的时间都会增加,因为每批工作负载的执行效率变得更低。
1 mini2_res = train_sgd(.05 , 10 )
1 loss: 0.244, 0.002 sec/epoch
pytorch中可以直接调用自带函数
1 torch.optim.SGD(net.parameters(),{'lr' : 0.01 })
GD,SGD,Mini-Batch-GD对比
GD下降在每次更新时用所有样本
SGD在每次更新时用1个样本,可以看到多了随机两个字,随机也就是说用样本中的一个例子来近似所有的样本
Mini-Batch-GD在每次更新时用b个样本
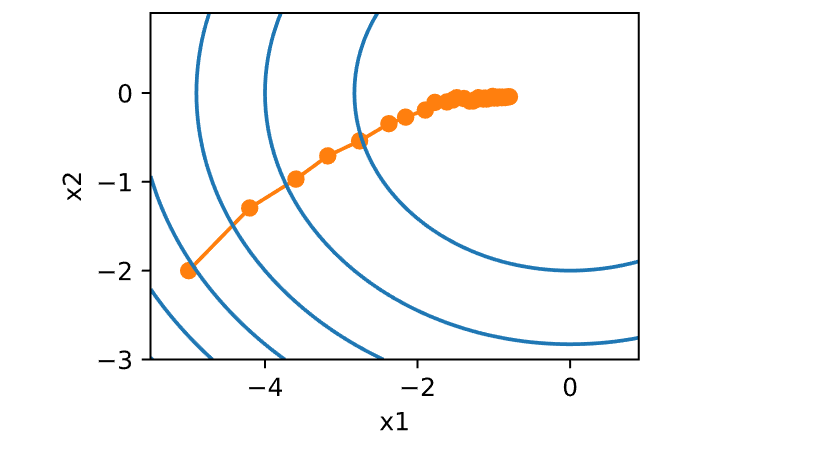
四、动量法(Momentum)
动量法通过引入动量项加速梯度下降,特别是处理高曲率、噪声梯度或错位梯度时效果显著。
f (x ) = 0.1x 1 2 + 2x 2 2 .
f (0, 0) 有最小值,该函数在x 1 非常 平坦。
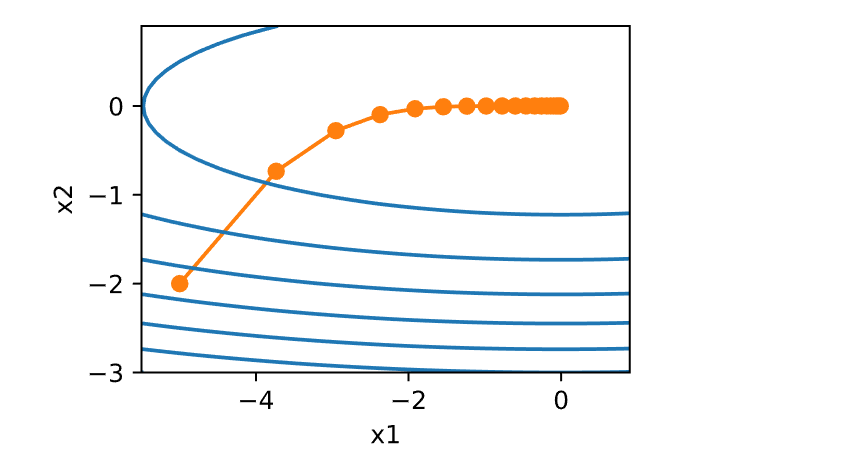
1 2 3 4 5 6 7 eta = 0.4 def f_2d (x1, x2 ):return 0.1 * x1 ** 2 + 2 * x2 ** 2 def gd_2d (x1, x2, s1, s2 ):return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0 , 0 )
1 epoch 20, x1: -0.943467, x2: -0.000073
从构造来看,x 2 x 1 x 2 x 1 x 1 x 2 0.4 略微提高到0.6 ,也会发生变化。x 1
1 2 eta = 0.6
1 epoch 20, x1: -0.387814, x2: -1673.365109
动量法 (momentum)能够解决上面描述的梯度下降问题。观察上面的优化轨迹,觉得计算过去的平均梯度效果会很好。毕竟,在x 1 x 2 v t g t
对于β = 0
1 2 3 4 5 6 7 def momentum_2d (x1, x2, v1, v2 ):0.2 * x14 * x2return x1 - eta * v1, x2 - eta * v2, v1, v20.6 , 0.5
1 epoch 20, x1: 0.007188, x2: 0.002553
可以看到,尽管学习率与以前使用的相同,动量法仍然很好地收敛了。让β = 0.25
1 2 eta, beta = 0.6 , 0.25
1 epoch 20, x1: -0.126340, x2: -0.186632
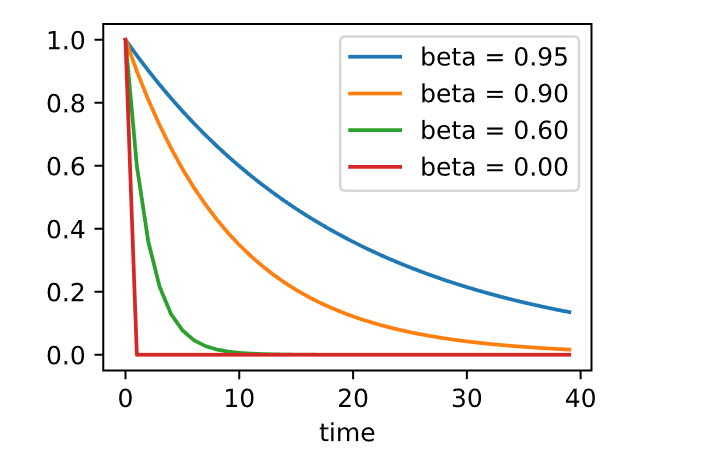
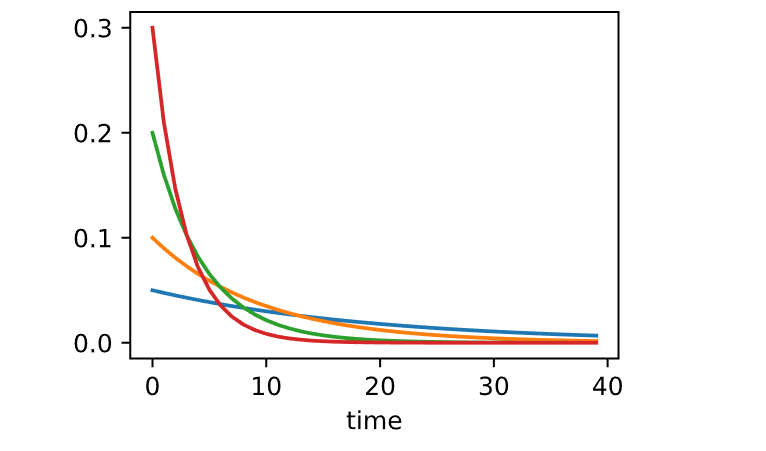
4.1 有效样本权重
η β
1 2 3 4 5 6 7 set_figsize()0.95 , 0.9 , 0.6 , 0 ]for beta in betas:40 ).detach().numpy()f'beta = {beta:.2 f} ' )'time' )
相比于小批量随机梯度下降,动量方法需要维护一组辅助变量,即速度。它与梯度以及优化问题的变量具有相同的形状。称这些变量为states。
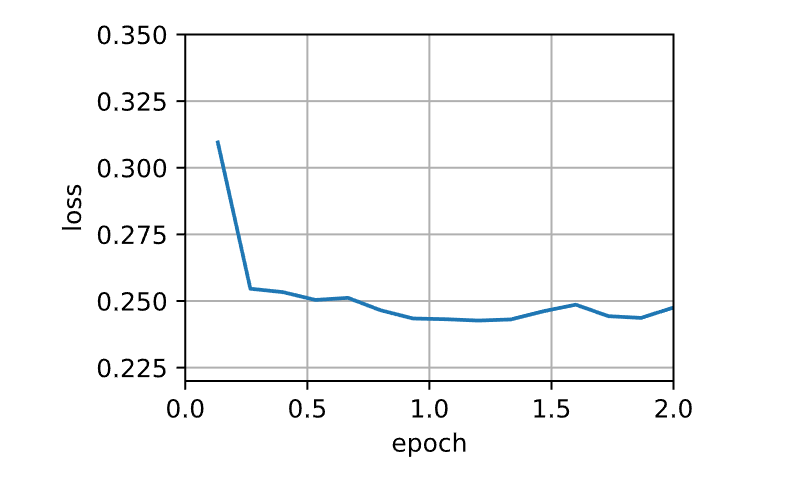
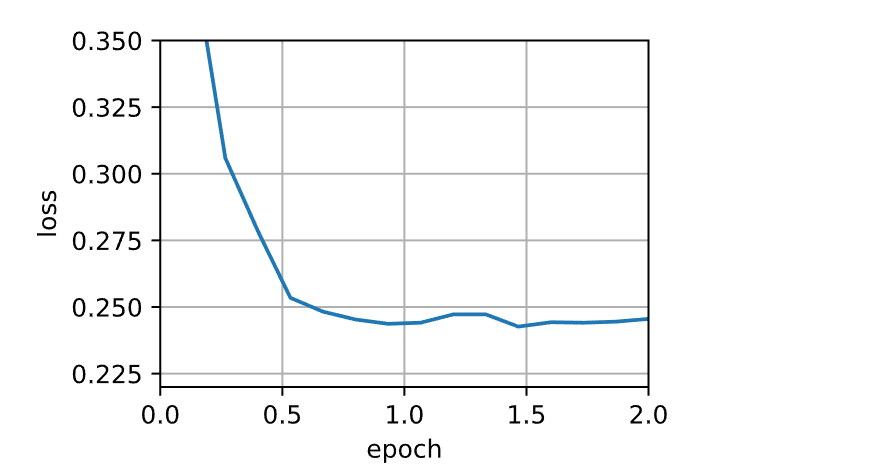
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 def init_momentum_states (feature_dim ):1 ))1 )return (v_w, v_b)def sgd_momentum (params, states, hyperparams ):for p, v in zip (params, states):with torch.no_grad():'momentum' ] * v + p.grad'lr' ] * vdef train_momentum (lr, momentum, num_epochs=2 ):'lr' : lr, 'momentum' : momentum}, data_iter,10 )0.02 , 0.5 )
1 loss: 0.242, 0.003 sec/epoch
将动量超参数momentum增加到0.9时,它相当于有效样本数量增加到0.01 ,以确保可控。
1 train_momentum(0.01 , 0.9 )
1 loss: 0.247, 0.003 sec/epoch
降低学习率进一步解决了任何非平滑优化问题的困难,将其设置为0.005 会产生良好的收敛性能。
1 train_momentum(0.005 , 0.9 )
1 loss: 0.244, 0.004 sec/epoch
pytorch中可以直接调用自带函数
1 torch.optim.SGD(net.parameters(), {'lr' : 0.005 , 'momentum' : 0.9 })
总结 *
动量法用过去梯度的平均值来替换梯度,这大大加快了收敛速度。 *
对于无噪声梯度下降和嘈杂随机梯度下降,动量法都是可取的。 *
动量法可以防止在随机梯度下降的优化过程停滞的问题。 *
由于对过去的数据进行了指数降权,有效梯度数为v
4.2. Nesterov
加速梯度(Nesterov Accelerated Gradient,NAG)
NAG 是动量法的改进版,通过计算未来位置的梯度来调整当前速度。
更新规则
v t β v t − 1β )∇θ J (θ − η β v t − 1θ = θ − η v t
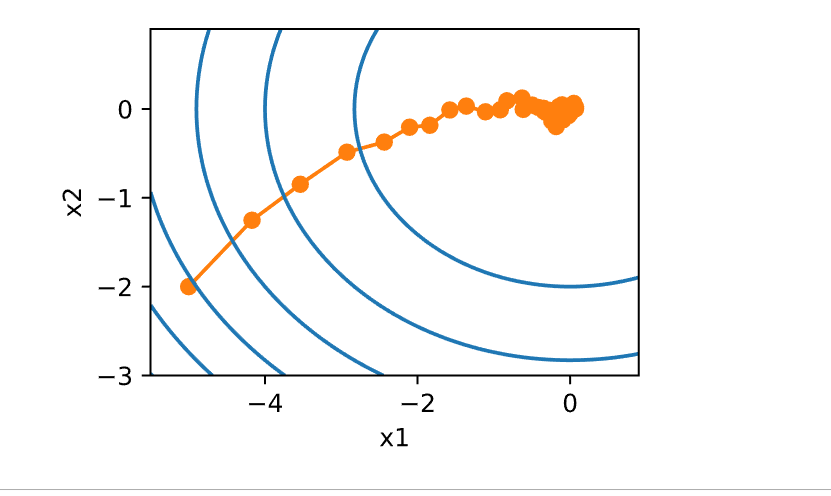
五、自适应梯度算法(Adagrad)
Adagrad
通过调整每个参数的学习率,使得稀疏参数更新较大,频繁参数更新较小。使用变量s t
在这里,操作是按照坐标顺序应用。也就是说,v 2 v i 2 u ⋅ v u i v i η ϵ 0 。最后,初始化s 0 = 0
就像在动量法中需要跟踪一个辅助变量一样,在AdaGrad算法中,允许每个坐标有单独的学习率。与SGD算法相比,这并没有明显增加AdaGrad的计算代价,因为主要计算用在l (y t f (x t w ))
在s t s t
f (x ) = 0.1x 1 2 + 2x 2 2 .
使用与之前相同的学习率来实现AdaGrad算法,即η = 0.4s t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 def adagrad_2d (x1, x2, s1, s2 ):1e-6 0.2 * x1, 4 * x22 2 return x1, x2, s1, s2def f_2d (x1, x2 ):return 0.1 * x1 ** 2 + 2 * x2 ** 2 0.4
1 epoch 20, x1: -2.382563, x2: -0.158591
具体实现
同动量法一样,AdaGrad算法需要对每个自变量维护同它一样形状的状态变量。
1 2 3 4 5 6 7 8 9 10 11 12 def init_adagrad_states (feature_dim ):1 ))1 )return (s_w, s_b)def adagrad (params, states, hyperparams ):1e-6 for p, s in zip (params, states):with torch.no_grad():'lr' ] * p.grad / torch.sqrt(s + eps)
使用更大的学习率来训练模型
1 2 3 data_iter, feature_dim =get_data(batch_size=10 )'lr' : 0.1 }, data_iter, feature_dim);
1 loss: 0.244, 0.003 sec/epoch
pytorch中可以直接调用自带函数
1 torch.optim.Adagrad(net.parameters(),{'lr' : 0.1 })
小结
AdaGrad算法会在单个坐标层面动态降低学习率。
AdaGrad算法利用梯度的大小作为调整进度速率的手段:用较小的学习率来补偿带有较大梯度的坐标。
如果优化问题的结构相当不均匀,AdaGrad算法可以帮助缓解扭曲。
AdaGrad算法对于稀疏特征特别有效,在此情况下由于不常出现的问题,学习率需要更慢地降低。
在深度学习问题上,AdaGrad算法有时在降低学习率方面可能过于剧烈。
六、RMSprop
RMSprop 通过指数加权平均来控制历史梯度平方和的增长,改进了 Adagrad
的学习率衰减问题。
6.1 算法
更新方程
常数ϵ > 010−6 ,以确保不会因除以零或步长过大而受到影响。鉴于这种扩展,现在可以自由控制学习率η s t
同momentum一样,使用1 且观测值的半衰期为γ −1 γ
1 2 3 4 5 6 set_figsize()0.95 , 0.9 , 0.8 , 0.7 ]for gamma in gammas:40 ).detach().numpy()1 -gamma) * gamma ** x, label=f'gamma = {gamma:.2 f} ' )'time' );
将学习率提高到2 ,可以看到更好的表现。这已经表明,即使在无噪声的情况下,学习率的降低可能相当剧烈,需要确保参数能够适当地收敛。
1 2 eta = 2
1 epoch 20, x1: -0.002295, x2: -0.000000
6.2 代码实现
依然使用二次函数f (x ) = 0.1x 1 2 + 2x 2 2 adagrad中,当使用学习率为0.4的Adagrad算法时,变量在算法的后期阶段移动非常缓慢,因为学习率衰减太快。RMSProp算法中不会发生这种情况,因为η
1 2 3 4 5 6 7 8 9 10 11 12 13 def rmsprop_2d (x1, x2, s1, s2 ):0.2 * x1, 4 * x2, 1e-6 1 - gamma) * g1 ** 2 1 - gamma) * g2 ** 2 return x1, x2, s1, s2def f_2d (x1, x2 ):return 0.1 * x1 ** 2 + 2 * x2 ** 2 0.4 , 0.9
1 epoch 20, x1: -0.010599, x2: 0.000000
在深度网络中实现RMSProp算法
1 2 3 4 5 6 7 8 9 10 11 12 def init_rmsprop_states (feature_dim ):1 ))1 )return (s_w, s_b)def rmsprop (params, states, hyperparams ):'gamma' ], 1e-6 for p, s in zip (params, states):with torch.no_grad():1 - gamma) * torch.square(p.grad)'lr' ] * p.grad / torch.sqrt(s + eps)
将初始学习率设置为0.01,加权项γ s 1/(1 − γ ) = 10 次平方梯度观测值的平均值。
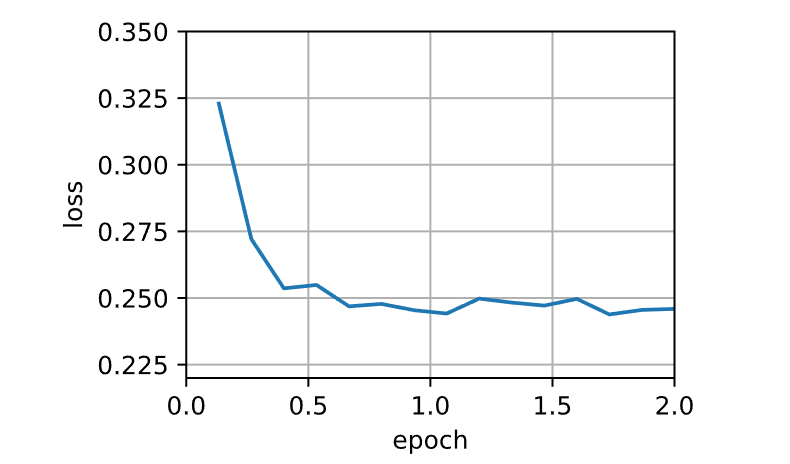
1 2 3 data_iter, feature_dim = get_data(batch_size=10 )'lr' : 0.01 , 'gamma' : 0.9 }, data_iter, feature_dim);
1 loss: 0.242, 0.004 sec/epoch
pytorch中可以直接调用自带函数
1 torch.optim.RMSprop(net.parameters(),{'lr' : 0.01 , 'alpha' : 0.9 })
七、Adadelta
Adadelta是AdaGrad的另一种变体,主要区别在于前者减少了学习率适应坐标的数量。此外,广义上Adadelta被称为没有学习率,因为它使用变化量本身作为未来变化的校准。
7.1 Adadelta算法
简而言之,Adadelta使用两个状态变量,s t Δ x t
以下是Adadelta的技术细节。鉴于参数du jour是ρ RMSprop类似的以下泄漏更新:
s t ρ s t − 1ρ )g t 2 .
与RMSprop的区别在于,使用重新缩放的梯度g t ′
x t x t − 1g t ′ .
那么,调整后的梯度g t ′
其中Δ x t − 1g t ′ Δ x 0 0 ,然后在每个步骤中使用g t ′
Δ x t ρ Δ x t − 1ρ )g t ′ 2 ,
和ϵ 10−5 这样的小值)是为了保持数字稳定性而加入的。
7.2 代码实现
Adadelta需要为每个变量维护两个状态变量,即s t Δ x t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def init_adadelta_states (feature_dim ):1 )), torch.zeros(1 )1 )), torch.zeros(1 )return ((s_w, delta_w), (s_b, delta_b))def adadelta (params, states, hyperparams ):'rho' ], 1e-5 for p, (s, delta) in zip (params, states):with torch.no_grad():1 - rho) * torch.square(p.grad)1 - rho) * g * g
对于每次参数更新,选择ρ = 0.9
1 2 3 data_iter, feature_dim = get_data(batch_size=10 )'rho' : 0.9 }, data_iter, feature_dim);
1 loss: 0.247, 0.003 sec/epoch
pytorch中可以直接调用自带函数
1 torch.optim.Adadelta(net.parameters(), {'rho' : 0.9 })
八、Adam(Adaptive Moment
Estimation)
Adam 结合了动量法和 RMSprop
的优点,既考虑了一阶矩(动量)又考虑了二阶矩(历史梯度平方和)。
8.1 算法
Adam算法的关键组成部分之一是:它使用指数加权移动平均值来估算梯度的动量和二次矩,即它使用状态变量
这里β 1 β 2 β 1 = 0.9β 2 = 0.999v 0 = s 0 = 0
有了正确的估计,现在可以写出更新方程。首先,以非常类似于RMSProp算法的方式重新缩放梯度以获得
与RMSProp不同,更新使用动量ϵ = 10−6
最后,简单更新:
x t x t − 1g t ′ .
回顾Adam算法,它的设计灵感很清楚:首先,动量和规模在状态变量中清晰可见,它们相当独特的定义使我们移除偏项(这可以通过稍微不同的初始化和更新条件来修正)。其次,RMSProp算法中两项的组合都非常简单。最后,明确的学习率η
8.2 实现
将时间步t hyperparams字典中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def init_adam_states (feature_dim ):1 )), torch.zeros(1 )1 )), torch.zeros(1 )return ((v_w, s_w), (v_b, s_b))def adam (params, states, hyperparams ):0.9 , 0.999 , 1e-6 for p, (v, s) in zip (params, states):with torch.no_grad():1 - beta1) * p.grad1 - beta2) * torch.square(p.grad)1 - beta1 ** hyperparams['t' ])1 - beta2 ** hyperparams['t' ])'lr' ] * v_bias_corr / (torch.sqrt(s_bias_corr)'t' ] += 1
用以上Adam算法来训练模型,这里使用η = 0.01
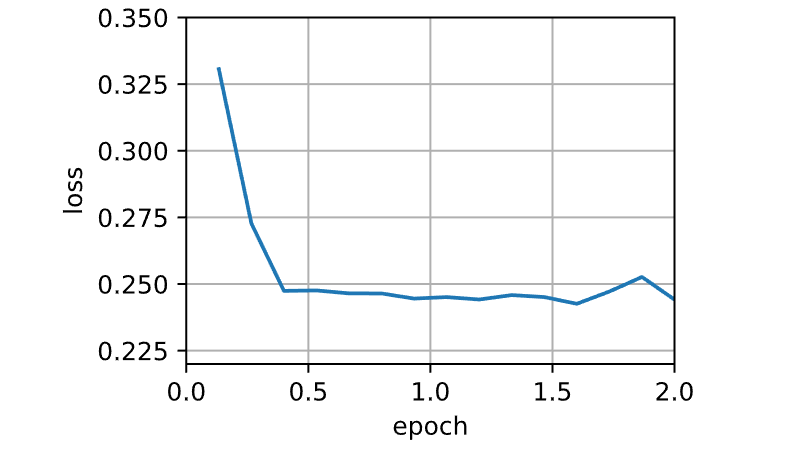
1 2 3 data_iter, feature_dim = get_data(batch_size=10 )'lr' : 0.01 , 't' : 1 }, data_iter, feature_dim);
1 loss: 0.243, 0.003 sec/epoch
8.3 Yogi
Adam算法也存在一些问题: 即使在凸环境下,当s t ADAPTIVE FEDERATED
OPTIMIZATION 为s t
s t s t − 1β 2 )(g t 2 − s t − 1
每当g t 2 s t g t 2 − s t − 1g t 2 ⊙ sgn (g t 2 − s t − 1
s t s t − 1β 2 )g t 2 ⊙ sgn (g t 2 − s t − 1
论文中,作者还进一步建议用更大的初始批量来初始化动量,而不仅仅是初始的逐点估计。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def yogi (params, states, hyperparams ):0.9 , 0.999 , 1e-3 for p, (v, s) in zip (params, states):with torch.no_grad():1 - beta1) * p.grad1 - beta2) * torch.sign(1 - beta1 ** hyperparams['t' ])1 - beta2 ** hyperparams['t' ])'lr' ] * v_bias_corr / (torch.sqrt(s_bias_corr)'t' ] += 1 10 )'lr' : 0.01 , 't' : 1 }, data_iter, feature_dim);
1 loss: 0.246, 0.003 sec/epoch
小结
Adam算法将许多优化算法的功能结合到了相当强大的更新规则中。
Adam算法在RMSProp算法基础上创建的,还在小批量的随机梯度上使用EWMA。
在估计动量和二次矩时,Adam算法使用偏差校正来调整缓慢的启动速度。
对于具有显著差异的梯度,可能会遇到收敛性问题。可以通过使用更大的小批量或者切换到改进的估计值s t
8.4 选择优化算法的建议
简单问题 :对简单的、非高维度数据,批量梯度下降和
SGD 通常已经足够。有噪声的梯度 :使用动量法或 NAG。稀疏数据 :Adagrad 和 RMSprop 是不错的选择。深度神经网络 :Adam 和其变种(如
AdamW、Nadam、AMSGrad)通常表现更好。
九、学习率调度器
选择一个稍微现代化的LeNet版本(激活函数使用relu而不是sigmoid,池化层使用最大池化层而不是平均池化层),并应用于Fashion-MNIST数据集。
定义模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 from torch.optim import lr_schedulerfrom torch import nnimport torchvisionfrom torchvision import transformsdef net_fn ():1 , 6 , kernel_size=5 , padding=2 ), nn.ReLU(),2 , stride=2 ),6 , 16 , kernel_size=5 ), nn.ReLU(),2 , stride=2 ),16 * 5 * 5 , 120 ), nn.ReLU(),120 , 84 ), nn.ReLU(),84 , 10 ))return model
评估函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def try_gpu (i=0 ): """如果存在,则返回gpu(i),否则返回cpu()""" if torch.cuda.device_count() >= i + 1 :return torch.device(f'cuda:{i} ' )return torch.device('cpu' )def try_all_gpus ():"""返回所有可用的GPU,如果没有GPU,则返回[cpu(),]""" f'cuda:{i} ' )for i in range (torch.cuda.device_count())]return devices if devices else [torch.device('cpu' )]def evaluate_accuracy_gpu (net, data_iter, device=None ):"""使用GPU计算模型在数据集上的精度""" if isinstance (net, nn.Module):eval () if not device:next (iter (net.parameters())).device2 )with torch.no_grad():for X, y in data_iter:if isinstance (X, list ):for x in X]else :return metric[0 ] / metric[1 ]
数据加载
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 def get_dataloader_workers (): """使用4个进程来读取数据""" return 4 def load_data_fashion_mnist (batch_size, resize=None ): """下载Fashion-MNIST数据集,然后将其加载到内存中""" if resize:0 , transforms.Resize(resize))"../data" , train=True , transform=trans, download=True )"../data" , train=False , transform=trans, download=True )return (data.DataLoader(mnist_train, batch_size, shuffle=True ,False ,256
训练
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 def train (net, train_iter, test_iter, num_epochs, loss, trainer, device, scheduler=None ):'epoch' , xlim=[0 , num_epochs],'train loss' , 'train acc' , 'test acc' ])for epoch in range (num_epochs):3 ) for i, (X, y) in enumerate (train_iter):with torch.no_grad():0 ], accuracy(y_hat, y), X.shape[0 ])0 ] / metric[2 ]1 ] / metric[2 ]if (i + 1 ) % 50 == 0 :len (train_iter),None ))1 , (None , None , test_acc))if scheduler:if scheduler.__module__ == lr_scheduler.__name__:else :for param_group in trainer.param_groups:'lr' ] = scheduler(epoch)print (f'train loss {train_loss:.3 f} , train acc {train_acc:.3 f} , ' f'test acc {test_acc:.3 f} ' )
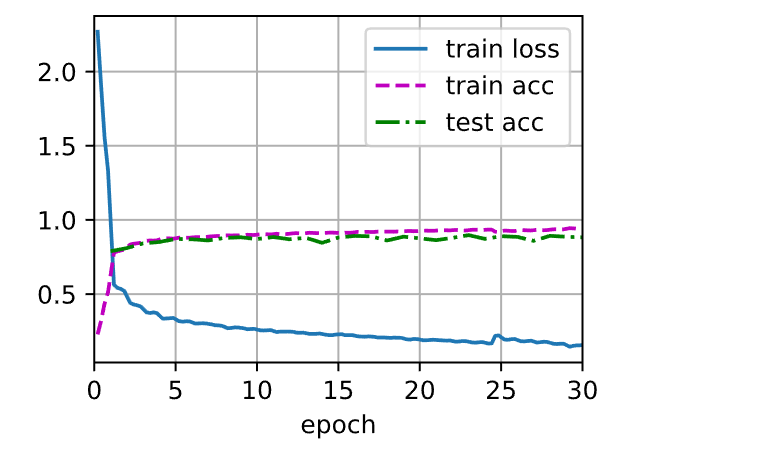
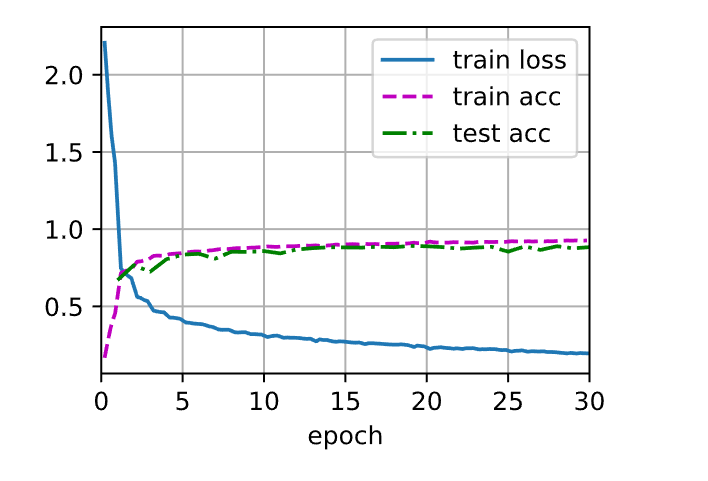
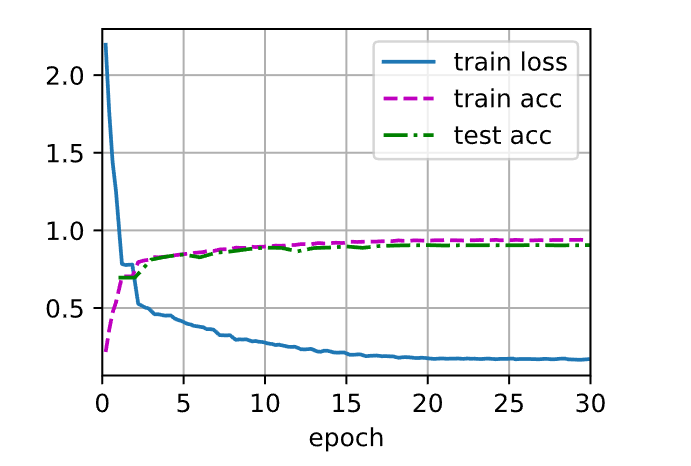
设学习率为0.3 并训练30 次迭代。留意在超过了某点、测试准确度方面的进展停滞时,训练准确度将如何继续提高。两条曲线之间的间隙表示过拟合。
1 2 3 4 lr, num_epochs = 0.3 , 30
1 train loss 0.157, train acc 0.940, test acc 0.882
9.1 学习率调度器
9.1.1 单因子调度器
多项式衰减的一种替代方案是乘法衰减,即η t + 1η t α α ∈ (0, 1)η t + 1η min , η t α )
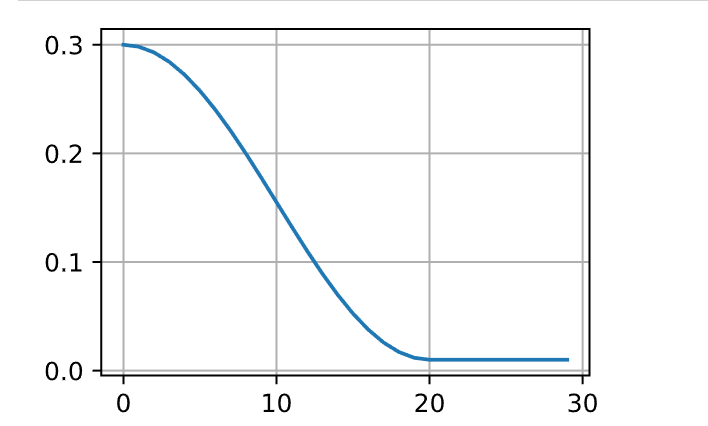
1 2 3 4 5 6 7 8 9 10 11 12 class FactorScheduler :def __init__ (self, factor=1 , stop_factor_lr=1e-7 , base_lr=0.1 ):self .factor = factorself .stop_factor_lr = stop_factor_lrself .base_lr = base_lrdef __call__ (self, num_update ):self .base_lr = max (self .stop_factor_lr, self .base_lr * self .factor)return self .base_lr0.9 , stop_factor_lr=1e-2 , base_lr=2.0 )50 ), [scheduler(t) for t in range (50 )])
9.1.2 多因子调度器
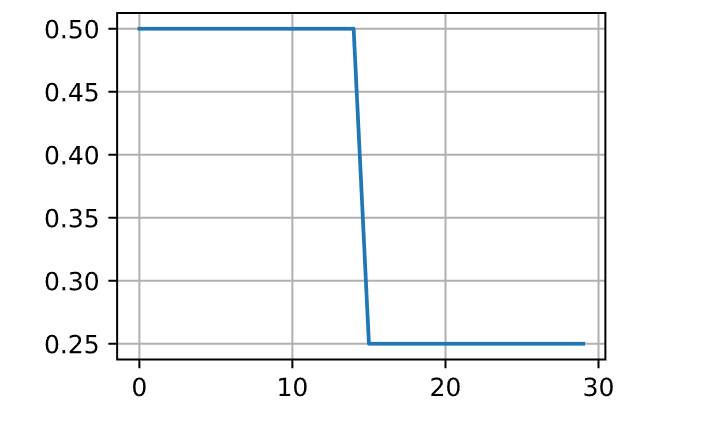
训练深度网络的常见策略之一是保持学习率为一组分段的常量,并且不时地按给定的参数对学习率做乘法衰减。具体地说,给定一组降低学习率的时间点,例如s = {5, 10, 20}t ∈ s η t + 1η t α
1 2 3 4 5 6 7 8 9 10 11 12 13 net = net_fn()30 0.5 )15 , 30 ], gamma=0.5 )def get_lr (trainer, scheduler ):0 ]return lrfor t in range (num_epochs)])
这种分段恒定学习率调度背后的直觉是,让优化持续进行,直到权重向量的分布达到一个驻点。此时,才将学习率降低,以获得更高质量的代理来达到一个良好的局部最小值。下面的例子展示了如何使用这种方法产生更好的解决方案。
1 2 train(net, train_iter, test_iter, num_epochs, loss, trainer, device,
1 train loss 0.195, train acc 0.927, test acc 0.884
9.1.3 余弦调度器
余弦调度器所依据的观点是:可能不想在一开始就太大地降低学习率,而且可能希望最终能用非常小的学习率来“改进”解决方案。这产生了一个类似于余弦的调度,函数形式如下所示,学习率的值在t ∈ [0, T ]
这里η 0 η T T t > T η T T = 20
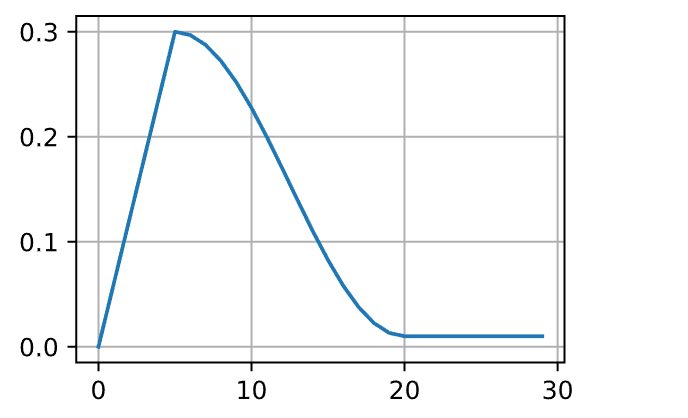
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class CosineScheduler :def __init__ (self, max_update, base_lr=0.01 , final_lr=0 , warmup_steps=0 , warmup_begin_lr=0 ):self .base_lr_orig = base_lrself .max_update = max_updateself .final_lr = final_lrself .warmup_steps = warmup_stepsself .warmup_begin_lr = warmup_begin_lrself .max_steps = self .max_update - self .warmup_stepsdef get_warmup_lr (self, epoch ):self .base_lr_orig - self .warmup_begin_lr) \float (epoch) / float (self .warmup_steps)return self .warmup_begin_lr + increasedef __call__ (self, epoch ):if epoch < self .warmup_steps:return self .get_warmup_lr(epoch)if epoch <= self .max_update:self .base_lr = self .final_lr + (self .base_lr_orig - self .final_lr) * (1 + math.cos(self .warmup_steps) / self .max_steps)) / 2 return self .base_lr20 , base_lr=0.3 , final_lr=0.01 )for t in range (num_epochs)])
在计算机视觉的背景下,这个调度方式可能产生改进的结果。
但请注意,如下所示,这种改进并不一定成立。
1 2 3 4 net = net_fn()0.3 )
1 train loss 0.180, train acc 0.933, test acc 0.899
9.1.4 预热
在某些情况下,初始化参数不足以得到良好的解。这对某些高级网络设计来说尤其棘手,可能导致不稳定的优化结果。对此,一方面,可以选择一个足够小的学习率,从而防止一开始发散,然而这样进展太缓慢。另一方面,较高的学习率最初就会导致发散。
解决这种困境的一个相当简单的解决方法是使用预热期,在此期间学习率将增加至初始最大值,然后冷却直到优化过程结束。为了简单起见,通常使用线性递增。这引出了如下表所示的时间表。
1 2 scheduler = CosineScheduler(20 , warmup_steps=5 , base_lr=0.3 , final_lr=0.01 )for t in range (num_epochs)])
观察前5个迭代轮数的性能,网络最初收敛得更好。
1 2 3 4 net = net_fn()0.3 )
1 train loss 0.170, train acc 0.938, test acc 0.905
预热可以应用于任何调度器,而不仅仅是余弦。A CLOSER LOOK AT DEEP LEARNING
HEURISTICS:LEARNING RATE RESTARTS, WARMUP AND
DISTILLA-TION 指出预热阶段限制了非常深的网络中参数的发散程度。在网络中那些一开始花费最多时间取得进展的部分,随机初始化会产生巨大的发散。
小结
在训练期间逐步降低学习率可以提高准确性,并且减少模型的过拟合。
在实验中,每当进展趋于稳定时就降低学习率,这是很有效的。从本质上说,这可以确保有效地收敛到一个适当的解,也只有这样才能通过降低学习率来减小参数的固有方差。
余弦调度器在某些计算机视觉问题中很受欢迎。
优化之前的预热期可以防止发散。
优化在深度学习中有多种用途。对于同样的训练误差而言,选择不同的优化算法和学习率调度,除了最大限度地减少训练时间,可以导致测试集上不同的泛化和过拟合量。
参考
常見梯度下降法 随机梯度下降(stochastic
gradient descent,SGD) Self-Attention Alec
Radford’s animations for optimization algorithms 李沐-动手学深度学习第二版 Optimization
Algorithms in Neural Networks Gradient
Descent Explained EfficientDL:
Mini-batch Gradient Descent Explained