贝叶斯分类器

1.贝叶斯公式

条件概率公式

设 A , B 是两个事件，且 P(B) > 0 ,则在事件 B 发生的条件下，事件 A 发生的条件概率(conditional probability)为：

全概率公式

如果事件 B₁, B₂, ⋯, B_n 满足 B_i ∩ B_j = ∅, i ≠ j     i, j = 1, 2, ⋯, n , 且 P(B_i) > 0, B₁ ∪ B₂ ∪ ⋯B_n = Ω ，设 A 为任意事件，则有:

上式即为全概率公式(formula of total probability)

全概率公式的意义在于，当直接计算 P(A) 较为困难,而 P(B_i), P(A|Bi) 的计算较为简单时，可以利用全概率公式计算 P(A)。思想就是，将事件 A 分解成几个小事件，通过求小事件的概率，然后相加从而求得事件A的概率，而将事件A进行分割的时候，不是直接对 A 进行分割，而是先找到样本空间 Ω 的一个个划分 B₁, B₂, ⋯, B_n ,这样事件 A 就被事件 AB₁, AB₂, ⋯, AB_n 分解成了 n 部分，而每一个 B_i 发生都可能导致 A 发生相应的概率是

P(A|B_i)

贝叶斯公式

与全概率公式解决的问题相反，贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因（事件 A 已经发生的条件下，分割中的小事件 B_i 的概率），设 B₁, B₂, ⋯, B_n 是样本空间 Ω 的一个划分，则对任一事件 A(P(A) > 0) ,有

上式即为贝叶斯公式(Bayes formula)， B_i 常被视为导致试验结果 A 发生的原因， P(B_i) 表示各种原因发生的可能性大小，故称先验概率； P(Bi|A) 则反映当试验产生了结果 A 之后，再对各种原因概率的新认识，故称后验概率。

2.朴素贝叶斯法

2.1 基本方法

设输入空间 𝒳 ⊆ Rⁿ 为 n 维向量的集合，输出空间为类标记集合𝒴 = {c₁, c₂, ⋯, c_K}.输入为特征向量 x ∈ 𝒳 ,输出为类标记(class label) y ∈ 𝒴 . X 是定义在输入空间 𝒳 上的随机向量， Y 是定义在输出空间 𝒴 上的随机变量。 P(X, Y) 是 X 和 Y 的联合概率分布。训练数据集

T = {(x₁, y₁), (x₂, y₂), ⋯, (x_N, y_N)}

由 P(X, Y) 独立同分布产生。

朴素贝叶斯法通过训练数据集学习联合概率分布 P(X, Y) .具体地，学习以下先验概率分布及条件概率分布。先验概率分布

P(Y = c_k),   k = 1, 2, ⋯, K

条件概率分布

P(X = x|Y = c_k) = P(X⁽¹⁾ = x⁽¹⁾, ⋯, X⁽ⁿ⁾ = x⁽ⁿ⁾|Y = c_k),   k = 1, 2, ⋯, K

于是学习到联合概率分布 P(X, Y) .

条件概率分布 P(X = x|Y = c_k) 有指数级数量的参数，其估计实际不可行的。事实上，假设 x^(j) 可取值有 S_j 个， j = 1, 2, ⋯, n,  Y 可取值有 K 个，那么参数个数为 .

朴素贝叶斯法对条件概率分布做了条件独立性的假设。由于这是一个较强的假设，朴素贝叶斯也由此得名。条件独立的假设是

朴素贝叶斯是生成模型，它学习到的是生成数据的机制。条件独立假设等价于用于分类的特征在类确定的条件下都是条件独立的。这个假设使朴素贝叶斯法变得简单，但有时会使分类的准确率降低。

朴素贝叶斯法分类时，对给定的输入 x ,通过学习到的模型计算后验概率分布

P(Y = c_k|X = x)

将后验概率最大的类作为 x 的类输出，后验概率计算根据贝叶斯定理进行

根据条件独立性假设可得

这便是朴素贝叶斯的基本公式，朴素贝叶斯分类器可表示为

其中分母对所有 c_k 都相同，所以上述公式等价于

y = f(x)arg max_ckP(Y = c_k)∏_jP(X^(j) = x^(j)|Y = c_k)

2.2 后验概率最大化含义

朴素贝叶斯法将实例分到后验概率最大的类中，这等价于期望风险最小化。假设选择0-1损失函数

其中 f(X) 是分类决策函数，则期望风险函数为

R_exp(f) = E[L(X, f(X))]

期望是对联合分布 P(X, Y) 取。由此取条件期望

为了使期望风险最小化，只需对 X = x 逐个极小化，由此得到:

由以上推导就得到了后验概率最大化准则

f(x) = arg max_ckP(c_k|X = x)

2.3 朴素贝叶斯参数估计

2.3.1 极大似然估计

在朴素贝叶斯法中，学习意味着估计

P(Y = c_k), P(X^(j) = x^(j)|Y = c_k)

可以应用极大似然估计法估计相应概率，则

设第 j 个特征 x^(j) 可能取值的集合为

{a_j1, a_j2, ⋯, a_jSj}

条件概率的极大似然估计

j = 1, 2, ⋯, n;   l = 1, 2, ⋯, S_j;   k = 1, 2, ⋯, K

式中， x_i^(j) 是第 i 个样本的第 j 个特征； a_jl 是第 j 个特征可取的第 l 个值； I 为指示函数。

2.3.2 贝叶斯估计

极大似然估计可能会出现所要估计的概率为0的情况。这时会影响到后验概率的计算结果，使分类产生偏差。使用贝叶斯估计可解决这一问题,如下：

其中 λ ≥ 0 .等价于在随机变量各个取值的频数上赋予一个正数 λ > 0 .当 λ = 0 时就是极大似然估计。常取 λ = 1 ，这时称为拉普拉斯平滑(Laplace smoothing).显然，对任何 l = 1, 2, ⋯, S_j;   k = 1, 2, ⋯, K 有

P_λ(X^(j) = a_jl|Y = c_k) > 0

先验概率的贝叶斯估计是

3.贝叶斯网路

3.1 定义

贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。

贝叶斯网络的有向无环图中的节点表示随机变量{X₁, X₂, ⋯, X_n}，它们可以是可观察到的变量，或隐变量、未知参数等。将有因果关系（或非条件独立）的变量或命题用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。连接两个节点的箭头代表此两个随机变量是具有因果关系，或非条件独立。

假设节点 E 直接影响到节点 H ，即 E → H ，则用从 E 指向 H 的箭头建立结点 E 到结点 H 的有向弧 (E, H) ，权值(即连接强度)用条件概率 P(H|E) 来表示，如下图所示：

把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖，用圈表示随机变量(random variables)，用箭头表示条件依赖(conditional dependencies)。

令 G = (I, E) 表示一个有向无环图(DAG)，其中 I 代表图形中所有的节点的集合，而 E 代表有向连接线段的集合，且令 x = (x_i), i ∈ I 为其有向无环图中的某一节点 i 所代表的随机变量，若节点 x 的联合概率可以表示成：

P(x) = ∏_i∈P(x_i|π_i)

则称 x 为相对于一有向无环图 G 的贝叶斯网络，其中， π_i 表示节点 i 之“因”，或称 π_i 是 i 的父节点集。

于任意的随机变量，其联合概率可由各自的局部条件概率分布相乘而得出：

P(x₁, ⋯, x_K) = P(x_K|x₁, ⋯, x_K − 1)⋯P(x₂|x₁)P(x₁)

3.2 结构

给定如下图所示的一个贝叶斯网络：

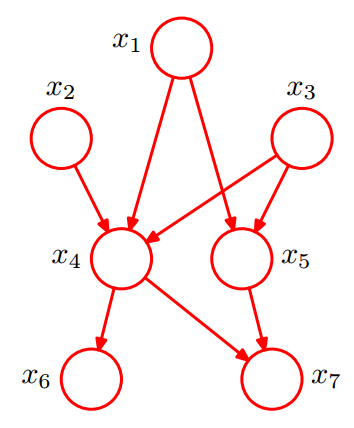
则其联合分布为:

P(x₁)P(x₂)P(x₃)P(x₄|x₁, x₂, x₃)P(x₅|x₁, x₃)P(x₆|x₄)P(x₇|x₄, x₅)

贝叶斯网络中三个变量之间的典型依赖关系有：同父结构(tail-to-tail),V型结构(head-to-head),顺序结构(head-to-tail).

tail-to-tail

如下图为tail-to-tail类型:

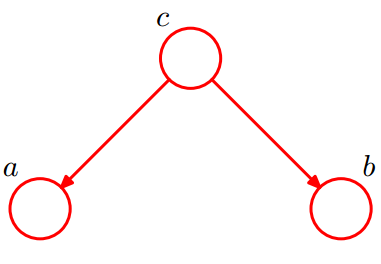
考虑 c 未知，跟 c 已知这两种情况：

在 c 未知的时候，有：

P(a, b, c) = P(c)P(a|c)P(b|c)

此时，没法得出 P(a, b) = P(a)P(b) ，即 c 未知时，a, b 不独立。

在 c 已知的时候，有：

c 已知时，a, b 独立。

所以，在 c 给定的条件下，a, b 被阻断(blocked)，是独立的，称之为tail-to-tail条件独立，对应本节中最开始那张图中的“ x₆ 和 x₇ 在 x₄ 给定的条件下独立”。

head-to-head

如下图为head-to-head类型:

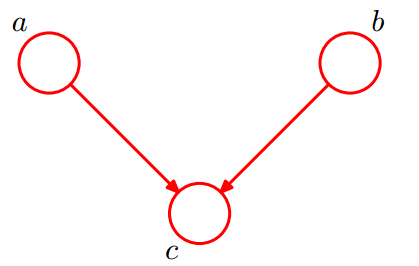
联合分布为:

P(a, b, c) = P(a)P(b)P(c|a, b)

有:

∑_cP(a, b, c) = ∑_cP(a)P(b)P(c|a, b) ⇒ P(a, b) = P(a)P(b)

即在 c 未知的条件下， a, b 被阻断(blocked)，是独立的，称之为head-to-head条件独立，对应本节中最开始那张图中的“ x₁, x₂ 独立”。

head-to-tail

如下图为head-to-tail类型:

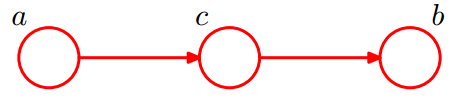
c 未知时，有：

P(a, b, c) = P(a)P(c|a)P(b|c) ⇏ P(a, b) = P(a)P(b)

即 c 未知时，a, b 不独立。

c 已知时，有：

P(a, c) = P(a)P(c|a) = P(c)P(a|c)

则有：

所以，在 c 给定的条件下，a, b 被阻断(blocked)，是独立的，称之为head-to-tail条件独立。

这个head-to-tail其实就是一个链式网络，如下图所示：

在 给定的条件下， x_i + 1 的分布和 x₁, x₂, ⋯, x_i − 1 条件独立.也就是说 x_i + 1 的分布状态只和 x_i 有关，和其他变量条件独立。当前状态只跟上一状态有关，跟上一个状态之前的所有状态无关。这种顺次演变的随机过程，就叫做马尔科夫链（Markov chain）。即：

P(X_n + 1|X₀, X₁, ⋯, X_n) = P(X_n + 1|X_n)

广义的讲，对于任意的结点集 A, B, C ，考察所有通过 A 中任意结点到 B 中任意结点的路径，若要求 A, B 条件独立，则需要所有的路径都被阻断(blocked)，即满足下列两个前提之一：

1. A 和 B 的“head-to-tail型”和“tail-to-tail型”路径都通过 C ；

2. A 和 B 的“head-to-head型”路径不通过 C 以及 C 的子孙；

3.3 因子图

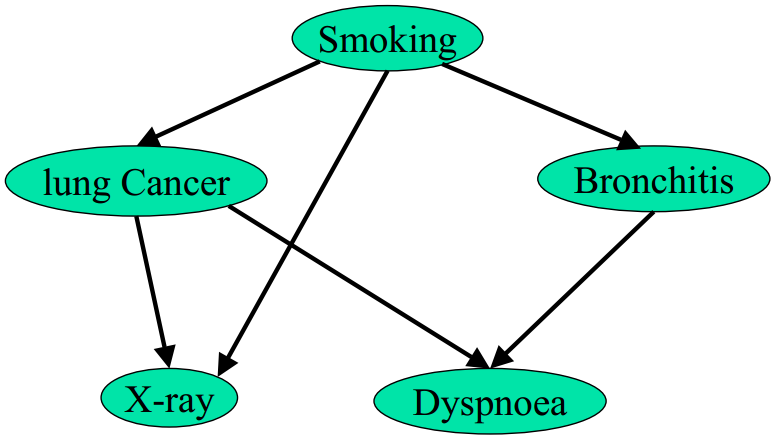
对于上图，在一个人已经呼吸困难（dyspnoea）的情况下，其抽烟（smoking）的概率是:

P(Smoking|Dyspnoea = yes) = ?

上式首先对联合概率关于 b, x, c 求和（在 d = 1 的条件下），从而消去 b, x, c ，得到 s 和 d = 1 的联合概率。由于 P(s) 和 d = 1, b, x, c 都没关系，所以，可以提到式子的最前面。而且 P(b|s) 和 x, c 没关系，所以，也可以把它提出来，放到 ∑_b 的后面，从而式子的右边剩下 ∑_x 和 ∑_c 。

3.3.1 因子图定义

将一个具有多变量的全局函数因子分解，得到几个局部函数的乘积，以此为基础得到的一个双向图叫做因子图（Factor Graph）。

例如，假定对函数 g(X₁, X₂, ⋯, X_n) ,有以下式子成立:

其对应的因子图 G = (X, F, E) 包括：

1.变量节点

X = {X₁, X₂, ⋯, X_n}

2.因子(函数)节点

F = {f₁, f₂, ⋯, f_m}

3.边 E ，边通过因式分解结果得到:在因子节点 f_i 和变量节点 X_k 之间存在边的充要条件是 X_K ∈ S_j 存在。

通俗来讲，所谓因子图就是对函数进行因子分解得到的一种概率图。一般内含两种节点：变量节点和函数节点。我们知道，一个全局函数通过因式分解能够分解为多个局部函数的乘积，这些局部函数和对应的变量关系就体现在因子图上。

如下全局函数，其因式分解方程为:

g(x₁, x₂, x₃, x₄, x₅) = f_A(x₁)f_B(x₂)f_C(x₁, x₂, x₃)f_D(x₃, x₄)f_E(x₃, x₅)

其中 f_A, f_B, f_C, f_D, f_E 为各函数，表示变量之间的关系，可以是条件概率也可以是其他关系（如马尔可夫随机场Markov Random Fields中的势函数）。

其对应的因子图为：

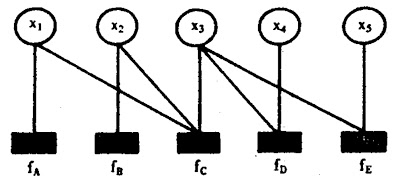
且上述因子图等价于：

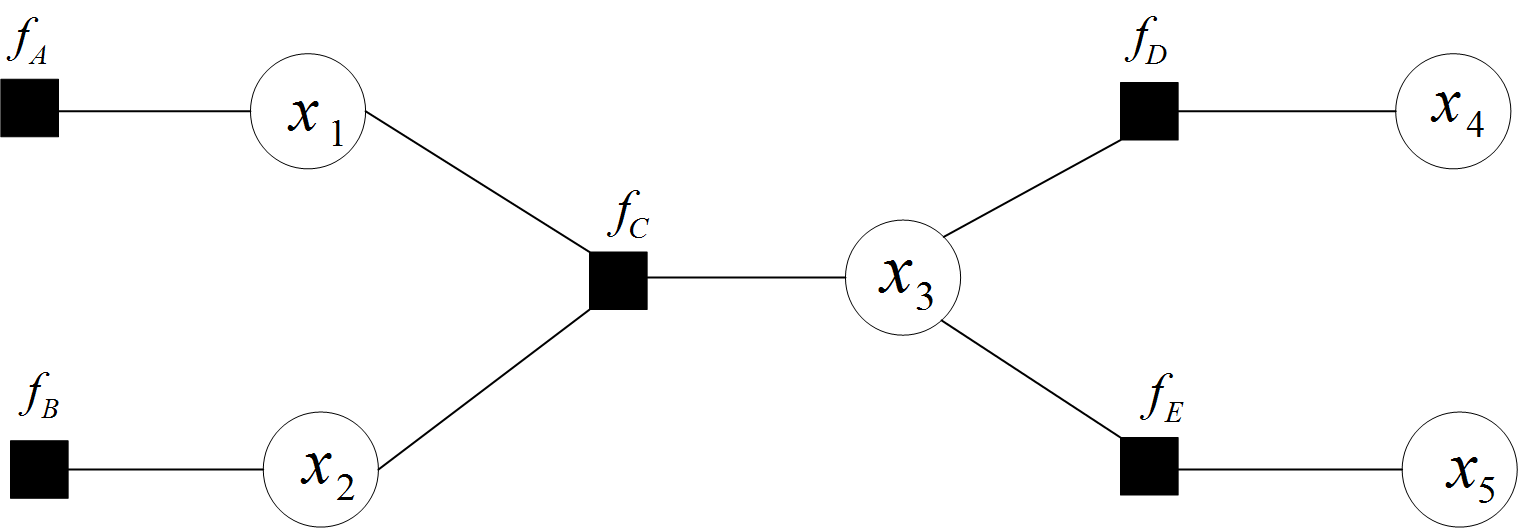
在因子图中，所有的顶点不是变量节点就是函数节点，边线表示它们之间的函数关系。因子图跟贝叶斯网络和马尔科夫随机场（Markov Random Fields）一样，也是概率图的一种。

• 有向图模型，又称作贝叶斯网络（Directed Graphical Models, DGM, Bayesian Network）。

• 但在有些情况下，强制对某些结点之间的边增加方向是不合适的。使用没有方向的无向边，形成了无向图模型（Undirected Graphical Model,UGM）, 又被称为马尔科夫随机场或者马尔科夫网络（Markov Random Field, MRF or Markov network）。

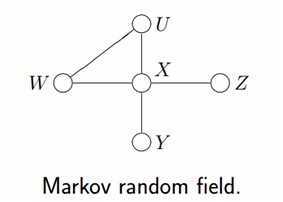
• 设 X = (X₁, X₂, ⋯, X_n) 和 Y = (Y₁, Y₂, ⋯, Y_m) 都是联合随机变量，若随机变量Y构成一个无向图 G = (V, E) 表示的马尔科夫随机场（MRF），则条件概率分布P(Y|X)称为条件随机场（Conditional Random Field, 简称CRF）。如下图所示，便是一个线性链条件随机场的无向图模型：

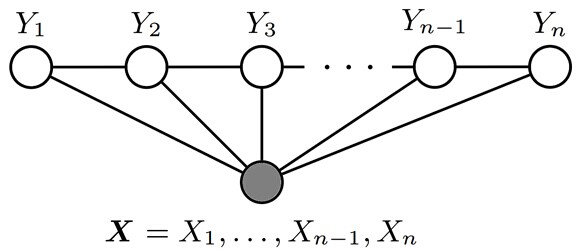
在概率图中，求某个变量的边缘分布是常见的问题。这问题有很多求解方法，其中之一就是把贝叶斯网络或马尔科夫随机场转换成因子图，然后用sum-product算法求解。换言之，基于因子图可以用sum-product 算法高效的求各个变量的边缘分布。

接下来首先说明如何把贝叶斯网络（和马尔科夫随机场），以及把马尔科夫链、隐马尔科夫模型转换成因子图后的情形，然后再来看如何利用因子图的sum-product算法求边缘概率分布。

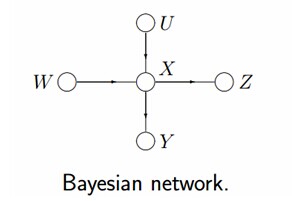
给定下图所示的贝叶斯网络或马尔科夫随机场：

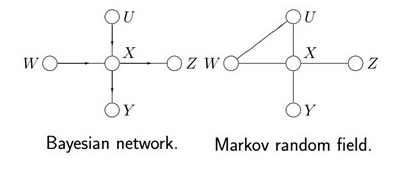
根据各个变量对应的关系，可得：

P(u, w, x, y, z) = P(u)P(w)P(x|u, w)P(y|x)P(z|x)

其对应的因子图为（以下两种因子图的表示方式皆可）：

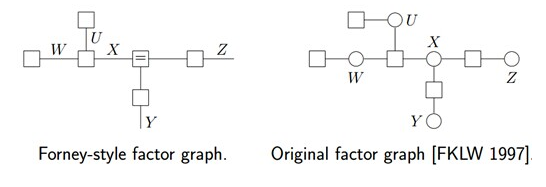
由上述例子总结出由贝叶斯网络构造因子图的方法：

• 贝叶斯网络中的一个因子对应因子图中的一个结点
• 贝叶斯网络中的每一个变量在因子图上对应边或者半边
• 结点 g 和边 x 相连当且仅当变量 x 出现在因子 g 中。

再比如，对于下图所示的由马尔科夫链转换而成的因子图：

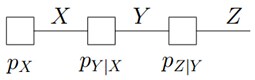有:

P_XYZ(x, y, z) = P_X(x)P_Y|X(y|x)P_Z|Y(z|y)

而对于如下图所示的由隐马尔科夫模型转换而成的因子图：

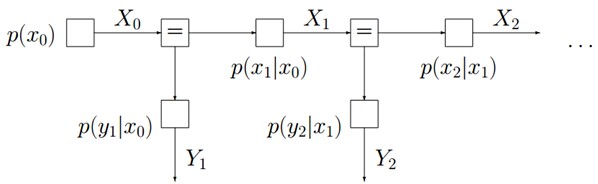
有:

3.3.2 Sum-product算法

对于下图所示的因子图：

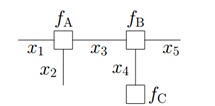
有:

f(x₁, x₂, x₃, x₄, x₅) = f_A(x₁, x₂, x₃)f_B(x₃, x₄, x₅)f_C(x₄)

联合概率分布和边缘概率分布:

• 联合概率表示两个事件共同发生的概率. A 与 B 的联合概率表示为 P(A ∩ B) 或者 P(A, B) .
• 边缘概率（又称先验概率）是某个事件发生的概率。边缘概率是这样得到的：在联合概率中，把最终结果中不需要的那些事件合并成其事件的全概率而消失（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率）。这称为边缘化（marginalization）。 A 的边缘概率表示为 P(A) , B 的边缘概率表示为 P(B) 。

某个随机变量 f_k 的边缘概率可由 x₁, x₂, x₃, ⋯, x_n 的联合概率求到，具体公式为：

对 x_k 外的其它变量的概率求和，最终剩下 x_k 的概率.

如果有

f(x₁, x₂, ⋯, f_n) = f₁(x₁)f₂(x₂)⋯f_n(x_n)

那么

f̄_k(x_k) = (∑_x1f₁(x₁))⋯(∑_xk − 1f_k − 1(x_k − 1))f_k(x_k)⋯(∑_xnf_n(x_n))

假定现在我们需要计算如下式子的结果：

同时，f 能被分解如下：

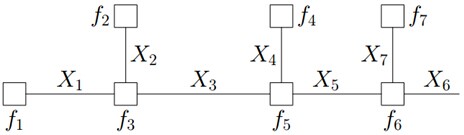
提取公因子:

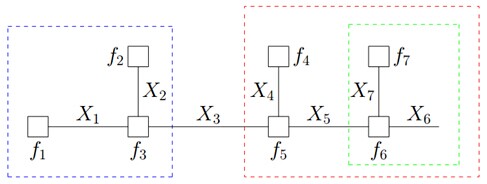
因为变量的边缘概率等于所有与他相连的函数传递过来的消息的积，所以计算得到：

f̄₃(x₃) = (∑_x1, x2f₁(x₁)f₂(x₂)f₃(x₁, x₂, x₃))(∑_x4, x5f₄(x₄)f₅(x₃, x₄, x₅)(∑_x6, x7f₆(x₅, x₆, x₇)f₇(x₇)))

可以发现，其中用到了类似“消息传递”的观点，且总共两个步骤。

第一步,对于 f 的分解图，根据蓝色虚线框、红色虚线框围住的两个box外面的消息传递：

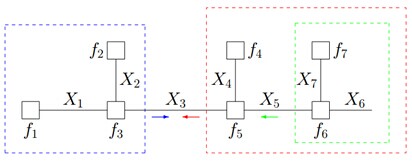
可得:

第二步,根据蓝色虚线框、红色虚线框围住的两个box内部的消息传递：

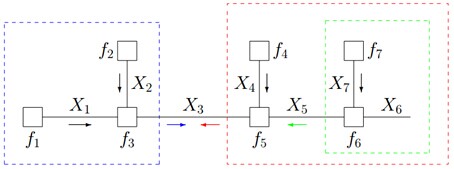
根据

μ⃗_X1(x₁) ≜  = f₁(x₁), μ⃗_X2(x₂) ≜  = f₂(x₂)

有

μ⃗_X3(x₃) = ∑_x1, x2μ⃗_X1(x₁)μ⃗_X2(x₂)f₃(x₁, x₂, x₃)

μ⃖_X5(x₅) = ∑_x6, x7μ⃗_X7(x₇)f₆(x₅, x₆, x₇)

μ⃖_X3(x₃) = ∑_x4, x5μ⃗_X4(x₄)μ⃖_X5(x₅)f₅(x₃, x₄, x₅)

上述计算过程将一个概率分布写成两个因子的乘积，而这两个因子可以继续分解或者通过已知得到。这种利用消息传递的观念计算概率的方法便是sum-product算法。基于因子图可以用sum-product算法可以高效的求各个变量的边缘分布。sum-product算法，也叫belief propagation，有两种消息：

• 一种是变量(Variable)到函数(Function)的消息：m_x → f ， 此时，变量到函数的消息为 m_x → f = 1 ,如下图所示:

• 另外一种是函数(Function)到变量(Variable)的消息： m_f → x , 此时，函数到变量的消息为： m_f → x = f(x) ,如下图所示：

sum-product算法的总体框架：

• 1.给定如下图所示的因子图：

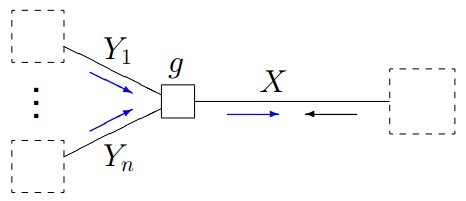
• 2.sum-product 算法的消息计算规则为：

μ⃗_X(x) = ∑_{y1, y2, ⋯, yn}g(x, y₁, y₂, ⋯, y_n)μ⃗_Y1(y₁)μ⃗_Y2(y₂)⋯μ⃗_Yn(y_n)

• 3.根据sum-product定理，如果因子图中的函数 f 没有周期，则有：

f̄_X(x) = μ⃗_X(x)μ⃖_X(x)

如果因子图是无环的，则一定可以准确的求出任意一个变量的边缘分布，如果是有环的，则无法用sum-product算法准确求出来边缘分布。

比如，下图所示的贝叶斯网络：

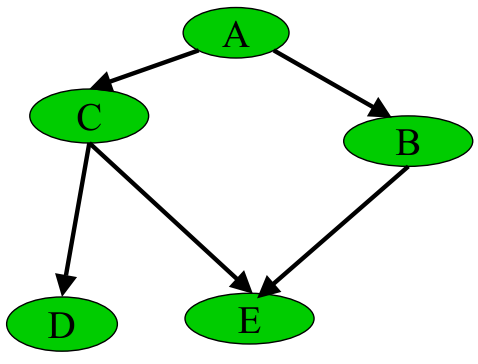
其转换成因子图后，为：

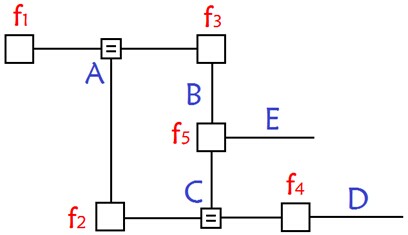
可以发现，若贝叶斯网络中存在“环”（无向），则因此构造的因子图会得到环。而使用消息传递的思想，这个消息将无限传输下去，不利于概率计算。

解决方法有3个：

第一种

删除贝叶斯网络中的若干条边，使得它不含有无向环.比如给定下图中左边部分所示的原贝叶斯网络，可以通过去掉C和E之间的边，使得它重新变成有向无环图，从而成为图中右边部分的近似树结构：

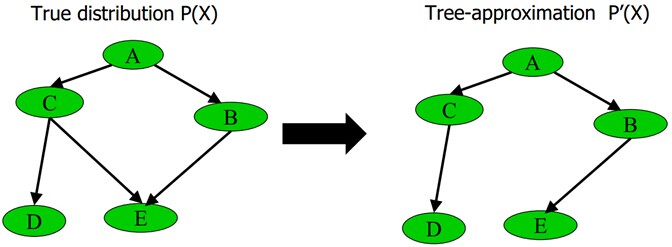
具体变换的过程为最大权生成树算法MSWT，通过此算法，这课树的近似联合概率 P^′(x) 和原贝叶斯网络的联合概率 P(x) 的相对熵最小。

MSWT建树过程:

• 1. 对于给定的分布 P(x) ，对于所有的 i ≠ j，计算联合分布

P(xi|xj)

• 2.使用第1步得到的概率分布，计算任意两个结点的互信息 I(X_i, Y_j) ，并把 I(X_i, Y_j) 作为这两个结点连接边的权值；
• 3.计算最大权生成树(Maximum-weight spanning tree)
  • 1. 初始状态： n 个变量(结点)，0条边
  • 2. 插入最大权重的边
  • 3. 找到下一个最大的边，并且加入到树中；要求加入后，没有环生成。否则，查找次大的边；
  • 4. 重复上述过程 c 过程直到插入了 n − 1 条边（树建立完成）
• 4. 选择任意结点作为根，从根到叶子标识边的方向；
• 5. 可以保证，这课树的近似联合概率 P^′(x) 和原贝叶斯网络的联合概率 P(x) 的相对熵最小。

第二种

重新构造没有环的贝叶斯网络

第三种

选择loopy belief propagation算法（可以简单理解为sum-product 算法的递归版本），此算法一般选择环中的某个消息，随机赋个初值，然后用sum-product算法，迭代下去，因为有环，一定会到达刚才赋初值的那个消息，然后更新那个消息，继续迭代，直到没有消息再改变为止。唯一的缺点是不确保收敛，当然，此算法在绝大多数情况下是收敛的。

此外，除了这个sum-product算法，还有一个max-product 算法。但只要弄懂了sum-product，也就弄懂了max-product 算法。因为max-product 算法就在上面sum-product 算法的基础上把求和符号换成求最大值max的符号即可！

最后，sum-product 和 max-product 算法也能应用到隐马尔科夫模型hidden Markov models上。

参考

1. 周志华 《机器学习》
2. 理解全概率公式与贝叶斯公式
3. 全概率公式、贝叶斯公式推导过程
4. 从贝叶斯方法谈到贝叶斯网络