神经网络(一)——线性神经网络

神经网络（Neural Network）是一种模仿人脑神经系统的计算模型，广泛应用于人工智能（AI）和机器学习领域。它的核心思想是通过多个简单的计算单元（神经元）之间的连接和权重调整，来处理和学习复杂的任务。

一、线性神经网络

尽管神经网络涵盖了更多更为丰富的模型，但是依然可以用描述神经网络的方式来描述线性模型，从而把线性模型看作一个神经网络。线性回归是一个单层神经网络。

如图所示的神经网络中，输入为，因此输入层中的输入数（或称为特征维度，feature dimensionality）为。网络的输出为，因此输出层中的输出数是1。由于模型重点在发生计算的地方，通常在计算层数时不考虑输入层。上图中神经网络的层数为1，称为单层神经网络。

对于线性回归，每个输入都与每个输出相连，将这种变换称为全连接层（fully-connected layer）或称为稠密层（dense layer）。

1.1 损失函数

线性回归向量乘法表示为：

在开始考虑如何用模型拟合（fit）数据之前，需要确定一个拟合程度的度量。损失函数（loss function）能够量化目标的实际值与预测值之间的差距。通常会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。回归问题中最常用的损失函数是平方误差函数。当样本的预测值为，其相应的真实标签为时，平方误差可以定义为以下公式：

1.1.1 损失函数总结

神经网络中的损失函数（Loss Function）是模型训练中至关重要的组成部分，它们用于衡量模型预测值与真实值之间的差异，指导模型参数的更新。根据任务类型的不同，常用的损失函数也有所不同。以下是详细的总结：

回归任务中的损失函数

均方误差（Mean Squared Error, MSE）：
- 公式：
- 解释：MSE是最常用的回归损失函数，它通过计算预测值与真实值之间差异的平方来衡量误差。平方项使得大误差被放大，从而对异常值更加敏感。
- 优点：对较大误差敏感，有助于模型更加关注大误差。
- 缺点：对异常值过于敏感，可能导致模型受少量异常值影响过大。
均绝对误差（Mean Absolute Error, MAE）：
- 公式：
- 解释：MAE计算预测值与真实值之间的绝对差异，对异常值不敏感，能提供更稳定的误差度量。
- 优点：对异常值不敏感，稳定性较好。
- 缺点：相比MSE，对较大误差的惩罚力度较小。
均方根误差（Root Mean Squared Error, RMSE）：
- 公式：
- 解释：RMSE是MSE的平方根，结果与原始数据的单位一致，便于解释。
- 优点：与MSE相同，对较大误差敏感，且结果单位与原始数据一致。
- 缺点：与MSE相同，对异常值敏感。
Huber损失（Huber Loss）：
- 公式：
- 解释：Huber损失结合了MSE和MAE的优点，对小误差采用平方误差，对大误差采用绝对误差，从而对异常值较为鲁棒。
- 优点：对异常值更加鲁棒，兼顾MSE和MAE的优点。
- 缺点：需要调整超参数。

分类任务中的损失函数

交叉熵损失（Cross-Entropy Loss）：
- 公式（对于二分类）：
- 公式（对于多分类）：
- 解释：交叉熵损失用于衡量预测概率分布与真实分布之间的差异，广泛用于分类任务。它能够有效地处理概率分布，并优化模型输出与真实标签的匹配程度。
- 优点：对概率分布的处理能力强，适用于分类问题。
- 缺点：对标签的概率值要求较高，预测值接近0或1时梯度变化剧烈。
二元交叉熵损失（Binary Cross-Entropy Loss）：
- 公式：
- 解释：专用于二分类问题，与一般的交叉熵损失类似，但针对二分类情况进行了优化。
- 优点：专门针对二分类任务，计算效率高。
- 缺点：对于多分类问题需要使用不同的损失函数。
稀疏分类交叉熵损失（Sparse Categorical Cross-Entropy Loss）：
- 解释：与多分类交叉熵类似，但标签为整数而非独热编码，计算效率更高，特别适用于大类数的分类任务。
- 优点：标签形式简洁，计算效率高。
- 缺点：只能用于稀疏标签场景。
Kullback-Leibler散度（Kullback-Leibler Divergence, KL散度）：
- 公式：
- 解释：用于衡量两个概率分布之间的差异，常用于需要匹配两个概率分布的任务，如变分自编码器（VAE）。
- 优点：能有效衡量两个分布之间的差异。
- 缺点：需要对概率分布进行细致建模，计算复杂。

特殊任务中的损失函数

对比损失（Contrastive Loss）：
- 解释：用于度量学习中的相似性度量，常用于Siamese网络。目标是将相似样本距离拉近，不相似样本距离拉远。
- 公式：
- 优点：适用于相似性度量任务。
- 缺点：需要成对训练数据，计算开销大。
Triplet Loss：
- 解释：用于度量学习，通过比较锚点样本（Anchor）与正样本（Positive）和负样本（Negative）之间的距离来优化嵌入空间。目标是使锚点与正样本距离小于锚点与负样本距离。
- 公式：
- 优点：能够有效地优化样本之间的相对距离。
- 缺点：需要精心选择样本对，训练复杂度较高。
CTC损失（Connectionist Temporal Classification Loss）：
- 解释：用于序列到序列学习，特别适用于不定长序列如语音识别，解决了对齐问题。
- 优点：能够处理不定长序列，特别适合语音和手写识别。
- 缺点：计算复杂度高，训练时间较长。
GAN中的损失函数：
- 生成器损失（Generator Loss）：
- 判别器损失（Discriminator Loss）：
- 解释：在生成对抗网络（GAN）中，生成器和判别器通过对抗训练互相改进。生成器试图生成逼真的样本以欺骗判别器，判别器则试图区分真实样本和生成样本。
- 优点：适用于生成任务，能够生成高质量的样本。
- 缺点：训练过程不稳定，易发生模式崩塌（mode collapse）。

总结

选择合适的损失函数是成功训练神经网络的关键步骤。不同的任务类型需要使用不同的损失函数，以便模型能够有效地学习和优化。在实际应用中，常常需要根据具体问题特点和需求来选择和调整损失函数，以达到最佳的效果。

1.2 梯度

为了寻找损失函数的最小值，会用到梯度。可以连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量。具体而言，设函数的输入是一个维向量，并且输出是一个标量。函数相对于的梯度是一个包含个偏导数的向量:

梯度下降（gradient descent）几乎可以优化所有深度学习模型。它通过不断地在损失函数递减的方向上更新参数来降低误差。梯度下降最简单的用法是计算损失函数（数据集中所有样本的损失均值）关于模型参数的导数（在这里也可以称为梯度）。但实际中的执行可能会非常慢：因为在每一次更新参数之前，必须遍历整个数据集。因此，通常会在每次需要计算更新的时候随机抽取一小批样本，这种变体叫做小批量随机梯度下降（minibatch stochastic gradient descent）。

1.2.1 小批量随机梯度下降

首先随机抽样一个小批量，它是由固定数量的训练样本组成的。然后，计算小批量的平均损失关于模型参数的导数。最后，将梯度乘以一个预先确定的正数，并从当前参数的值中减掉。

用下面的数学公式来表示这一更新过程（表示偏导数）：

总结一下，算法的步骤如下：
（1）初始化模型参数的值，如随机初始化；
（2）从数据集中随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代这一步骤。
对于平方损失和仿射变换，可以明确地写成如下形式:

公式中的和都是向量。表示每个小批量中的样本数，这也称为批量大小（batch size）。表示学习率（learning rate）。批量大小和学习率的值通常是手动预先指定，而不是通过模型训练得到的。这些可以调整但不在训练过程中更新的参数称为超参数（hyperparameter）。调参（hyperparameter tuning）是选择超参数的过程。超参数通常是根据训练迭代结果来调整的，而训练迭代结果是在独立的验证数据集（validation dataset）上评估得到的。

在训练了预先确定的若干迭代次数后（或者直到满足某些其他停止条件后），记录下模型参数的估计值，表示为。线性回归恰好是一个在整个域中只有一个最小值的学习问题。但是对像深度神经网络这样复杂的模型来说，损失平面上通常包含多个最小值。事实上，更难做到的是找到一组参数，这组参数能够在从未见过的数据上实现较低的损失，这一挑战被称为泛化（generalization）。

1.2.2 链式法则

在深度学习中，多元函数通常是复合（composite）的，所以难以应用上述任何规则来微分这些函数。但是，链式法则可以被用来微分复合函数。

对于单变量函数。假设函数和都是可微的，根据链式法则：

现在考虑一个更一般的场景，即函数具有任意数量的变量的情况。假设可微分函数有变量，其中每个可微分函数都有变量。是 $，$ 的函数。对于任意，链式法则给出：

1.2.3 自动微分

深度学习框架通过自动计算导数，即自动微分（automatic differentiation）来加快求导。实际中，根据设计好的模型，系统会构建一个计算图（computational graph），来跟踪计算是哪些数据通过哪些操作组合起来产生输出。自动微分使系统能够随后反向传播梯度。这里，反向传播（backpropagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。

对函数关于列向量求导:

import torch

x = torch.arange(4.0)

x.requires_grad_(True)  # 等价于x=torch.arange(4.0,requires_grad=True)
x.grad  # 默认值是None

y = 2 * torch.dot(x, x)

y.backward()
x.grad

1	`tensor([ 0., 4., 8., 12.])`

1.3 使用pytorch实现

import numpy as np
import torch
from torch.utils import data
from torch import nn

def synthetic_data(w, b, num_examples):  
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2

features, labels = synthetic_data(true_w, true_b, 1000)

#读取数据集
def load_array(data_arrays, batch_size, is_train=True):  
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

#定义模型
net = nn.Sequential(nn.Linear(2, 1))

#初始化模型参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

#定义损失函数
loss = nn.MSELoss()

#定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

1.3.1 训练过程

在每次迭代中，读取一小批量训练样本，并通过模型来获得一组预测。计算完损失后，开始反向传播，存储每个参数的梯度。最后，调用优化算法sgd来更新模型参数。

概括一下，就是执行以下循环：

初始化参数
重复以下训练，直到完成
- 计算梯度
- 更新参数

在每个迭代周期（epoch）中，使用data_iter函数遍历整个数据集，并将训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设为3和0.03。

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

1
2
3

epoch 1, loss 0.000226
epoch 2, loss 0.000095
epoch 3, loss 0.000096

二、Softmax回归

Softmax回归（Softmax Regression），也称为多项逻辑回归（Multinomial Logistic Regression），是一种广泛用于多分类问题的线性分类模型。它通过使用softmax函数将线性组合的输入值转换为概率分布，从而预测样本属于各个类别的概率。

与线性回归一样，softmax回归也是一个单层神经网络。由于计算每个输出、和取决于所有输入、、和，所以softmax回归的输出层也是全连接层。

2.1 模型结构

假设我们有一个分类任务，类别数为，输入特征向量为，权重矩阵为，每个是一个与输入向量长度相同的权重向量，偏置向量为。

1. 线性模型

对于每一个类别，计算线性组合：

得到一个未归一化的得分向量。

2. Softmax 函数

使用softmax函数将未归一化的得分向量转换为概率分布：

其中，表示输入样本属于类别的概率。是模型全连接层的输出，即输出为

2.2 对softmax函数求导

对softmax函数进行求导，第项输出对第项输入的偏导：

其中对进行求导结果为; 对进行求导分情况:

如果 ,求导结果为
如果 ,求导结果为 0

的导数为

所以时：

我们需要求导数，分两种情况讨论：和。

时：

将两种情况综合起来，softmax函数的导数可以表示为：

2.3 损失函数

为了训练Softmax回归模型，需要定义损失函数来衡量模型预测与真实标签之间的差异。常用的损失函数是交叉熵损失（Cross-Entropy Loss）。

1. 交叉熵损失函数

对于一个样本的交叉熵损失定义为：

其中，是模型预测的样本属于类别的概率，是真实的标签（使用独热编码表示）。

2.4 求解方法

为了最小化交叉熵损失函数，常用的优化方法是梯度下降及其变种（如随机梯度下降，Adam优化等）。需要计算损失函数对参数和的梯度。

1. 梯度计算

对输入的导数为,并将Softmax函数求导结果代入:

交叉熵 loss function 对 softmax function 输入的求导结果相当简单

应用

Softmax回归广泛应用于以下领域：
- 图像分类：例如MNIST手写数字识别。
- 文本分类：例如垃圾邮件检测、情感分析。
- 多类别问题：任何具有多个离散类别的分类任务。

2.5 pytorch实现

加载数据

import torch
from torch import nn
import torchvision
from torchvision import transforms
from d2l import torch as d2l
from IPython import display

batch_size = 256

def get_dataloader_workers():  
    """使用4个进程来读取数据"""
    return 4

def load_data_fashion_mnist(batch_size, resize=None):  
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=get_dataloader_workers()))

train_iter, test_iter = load_data_fashion_mnist(batch_size)

准确率评估

def accuracy(y_hat, y):
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

def evaluate_accuracy(net, data_iter): 
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:
            metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

绘图

class Accumulator:
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]


class Animator: 
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

模型定义

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

#没有将softmax概率传递到损失函数中,在交叉熵损失函数中传递未规范化的预测，并同时计算softmax及其对数
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=0.1)

训练

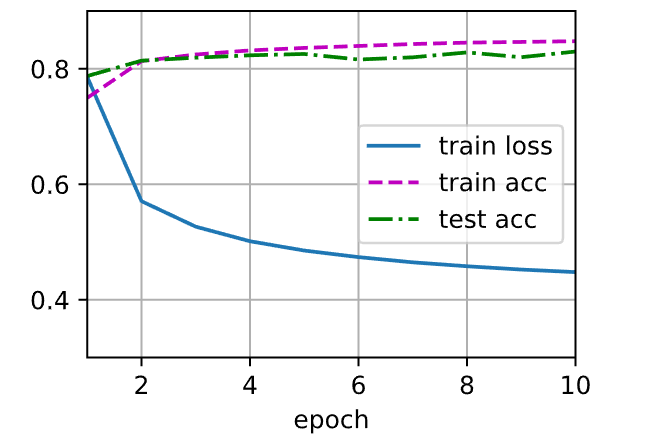
def train_epoch(net, train_iter, loss, updater): 
    """训练模型一个迭代周期（定义见第3章）"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

num_epochs = 10

def train1(net, train_iter, test_iter, loss, num_epochs, updater):  
    """训练模型（定义见第3章）"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

train1(net, train_iter, test_iter, loss, num_epochs, trainer)

参考

#DL #神经网络

神经网络(一)——线性神经网络

https://mztchaoqun.com.cn/posts/D54_NN/

作者

mztchaoqun

发布于

2024年12月30日

许可协议

神经网络(三)——卷积神经网络（Convolutional Neural Network）上一篇

Generative Model 下一篇