聚类

1.有监督学习与无监督学习

首先，看一下有监督学习(Supervised Learning)和无监督学(Unsupervised Learning)习的区别，给定一组数据(input，target)为 Z = (X, Y) 。

有监督学习: 最常见的是回归(regression)和分类(classification)。

• Regression: Y 是实数向量。回归问题，就是拟合 (X, Y) 的一条曲线，使得下式损失函数 L 最小。

L(f, (X, Y)) = ∥f(X) − Y∥²

• Classification: Y 是一个finite number，可以看做类标号。分类问题需要首先给定有label的数据训练分类器，故属于有监督学习过程。分类问题中，cost function L(X, Y) 是 X 属于类 Y 的概率的负对数。

L(f, (X, Y)) = −logf_Y(X),  f_i(X) = P(Y = i|X);  f_Y(X) ≥ 0,  ∑_if_i(X) = 1

无监督学习：无监督学习的目的是学习一个function f ，使它可以描述给定数据的位置分布 P(Z) 。 包括两种：密度估计(density estimation)和聚类(clustering).

• density estimation就是密度估计，估计该数据在任意位置的分布密度

• clustering就是聚类，将 Z 聚集几类（如K-Means），或者给出一个样本属于每一类的概率。由于不需要事先根据训练数据去训练聚类器，故属于无监督学习。

• PCA和很多deep learning算法都属于无监督学习。

聚类

聚类试图将数据集中的样本划分为若干个通常不相交的子集，每个子集称为一个“簇”(cluster).形式化地说，假定样本集

D = {x₁, x₂, ⋯, x_m}

包含 m 个无标记样本，每个样本 x_i = (x_i1; x_i2; ⋯; x_im) 是一个 n 维特征向量，则聚类算法将样本集 D 划分为 k 个不相交的簇

相应地，用

λ_j ∈ {1, 2, ⋯, k}

表示样本x_j的簇标记(cluster label),即x_j ∈ C_λj.于是，聚类的结果可以用包含 m 个元素的簇标记向量λ = (λ₁; λ₂; ⋯; λ_m)表示。

基于不同的学习策略有很多种类型的聚类学习算法，这里先讨论两个基本问题，性能度量和距离计算。

2.性能度量

聚类性能度量亦称聚类“有效性指标”(validity index).对于聚类结果，需要通过某种性能度量来评估其好坏。聚类结果应“簇内相似度”(intra-cluster similarity)高且“簇间相似度”(inter-cluster similarity)低。

聚类性能度量大致分为两类.一类是将聚类结果与某个参考模型(reference model)进行比较，称为外部指标(external index);另一类是直接考察聚类结果而不利用任何参考模型，称为内部指标(internal index).

对数据集 D ，假定通过聚类给出的簇划分结果为

C = {C₁, C₂, ⋯, C_k}

参考模型给出的簇划分为

C^* = {C₁^*, C₂^*, ⋯, C_k^*}

相应地，令λ, λ^*表示C, C^*对应的簇标记向量。定义

a = |SS|,   SS = {(x_i, x_j)|λ_i = lambda_j, λ_i^* = lambda_j^*, i < j}

b = |SD|,   SD = {(x_i, x_j)|λ_i = lambda_j, λ_i^*neqlambda_j^*, i < j}

c = |DS|,   DS = {(x_i, x_j)|λ_i ≠ lambda_j, λ_i^* = lambda_j^*, i < j}

d = |DD|,   DD = {(x_i, x_j)|λ_i ≠ lambda_j, λ_i^* ≠ lambda_j^*, i < j}

其中集合 SS 包含了在 C 中隶属于相同簇且在C^*中也隶属于相同簇的样本对；集合 SD 包含了在 C 中隶属于相同簇但在C^*中隶属于不同簇的样本对；……由于每个样本对 (x_i, x_j)(i < j) 仅能出现在一个集合中，因此有 a + b + c + d = m(m − 1)/2 成立。

基于上述式子可导出以下常用的聚类性能度量外部指标：

• Jaccard系数(Jaccard Coefficient,简称JC)

• FM指数(Fowlkes and Makkows Index,简称FMI)

• Rand指数(Rand Index,简称RI)

上述性能度量的结果值均在 [0, 1] 区间，值越大越好。

定义

diam(C) = max_{1 ≤ i < j ≤ |C|}dist(x_i, x_j)

d_min(C_i, C_j) = min_{xi ∈ Ci, xj ∈ Cj}dist(x_i, x_j)

d_cen(C_i, C_j) = dist(μ_i, μ_j)

其中, dist(⋅, ⋅) 用于计算两个样本之间的距离； μ 代表簇 C 的中心点

显然， avg(C) 对应簇 C 内样本间的平均距离； diam(C) 对应于簇 C 内样本的最远距离； d_min(C_i, C_j) 对应于簇 C_i , C_j 最近样本间的距离； d_cen(C_i, C_j) 对应于簇 C_i , C_j 中心点间的距离。

由上述各种距离的定义可以导出以下常用的聚类性能度量内部指标:

• DB指数(Davies_Bouldin Index,简称DBI)

• Dunn指数(Dunn Index,简称DI)

3.距离计算

dist(⋅, ⋅) 是距离度量，它有一些基本性质:

• 非负性： dist(x_i, x_j) ≥ 0 ;

• 同一性： dist(x_i, x_j) = 0 当且仅当 x_i = x_j ;

• 对称性： dist(x_i, x_j) = dist(x_i, x_j) ;

• 直递性： dist(x_i, x_j) ≤ dist(x_i, x_k) + dist(x_k, x_j) .

给定样本 x_i = (x_i1; x_i2; ⋯; x_in) 与 x_j = (x_j1; x_j2; ⋯; x_jn) ,则闵可夫斯基距离(Minkowski distance)为

对于 p ≥ 1 上式满足距离度量的基本性质。

p = 2 时该距离称为欧氏距离(Euclidean distance)

p = 2 时为曼哈顿距离(Manhattan distance)

对于1,2,3这类数字型之间的距离，可以直接算出1与2的距离比较近、与3的距离比较远，这样的属性称为有序属性(ordinal attribute);而对于与飞机，火车，轮船这样的离散属性则不能直接在属性值上计算距离，称为无序属性(non-ordinal attribute)。无属性距离不可用闵可夫斯基距离计算。

对无序属性可采用VDM(Value Difference Metric).令 m_u, a 表示在属性 u 上取值为 a 的样本个数， m_u, a, i 表示在第 i 个样本簇中在属性 u 上取值为 a 的样本数， k 为样本簇数，则属性 u 上两个离散值 a 与 b 之间的VDM为

将闵可夫斯基距离和VDM结合即可处理混合属性。假定有 n_c 个有序属性， n − n_c 个无序属性，令有序属性排列在无序属性之前，则

当样本空间中不同属性的重要性不同时，可使用加权距离(weihted distance),以加权闵可夫斯基距离为例

其中权重 w_i ≥ 0(i = 1, 2, ⋯, n) 表征不同属性的重要性，一般 .

通常相似度度量是基于某种形式的距离来定义的，距离越大，相似度越小。用于相似度度量的距离未必一定要满足距离度量的所有基本性质，尤其是直递性。不满足直递性的距离称为非度量距离(non-metric-distance).

4.原型聚类

原型聚类亦称基于原型的聚类(protorype-based clustering),此类算法假设聚类结构能通过一组原型刻画，算法先对原型进行初始化，然后对原型进行迭代更新。

4.1 k-means算法

给定样本集

D = {x₁, x₂, ⋯, x_m}

k-means算法针对聚类所得簇划分

C = {C₁, C₂, ⋯, C_k}

最小化平方误差

其中 μ_i 是簇 C_i 的均值向量。在一定程度上上式刻画了簇内样本围绕均值向量的紧密程度, E 值越小则簇内样本相似度越高。

最小化上述平方误差并不简单，找到最优解需要考察样本集 D 所有可能的簇划分，这是一个NP-Hard问题。因此，k-means算法采用了贪心策略，通过迭代优化近似解。

k-means算法流程：

输入:聚类簇数 k ,样本集D = {x₁, x₂, ⋯, x_m}

过程：

1. 从 D 中随机选择 k 个样本作为初始均值向量{μ₁, μ₂, ⋯, μ_k}

2. 令 C_i = ∅(1 ≤ i ≤ k)

3. 对于 j = 1, 2, ⋯, m 计算样本 x_j 与各均值向量 μ_i(1 ≤ i ≤ k) 的距离:

d_ji = ∥x_j − μ_i∥₂

根据距离最近的均值向量确定 x_j 的簇标记: λ_j = arg min_id_ji ; 将样本 x_j 划入相应的簇:C_λj = C_λj⋃{x_j};

4. 对于 i = 1, 2, ⋯, k 计算新均值向量 μ_i^′ ;如果 μ_i^′ ≠ μ_i 则将当前均值向量 μ_i 更新为 μ_i^′ ；否则保持当前均值向量不变

5. 重复步骤3,4，直到当前均值向量均未更新

输出：簇划分C = {C₁, C₂, ⋯, C_k}

K-Means 优缺点：

当结果簇是密集的，而且簇和簇之间的区别比较明显时，K-Means 的效果较好。对于大数据集，K-Means 是相对可伸缩的和高效的，它的复杂度是 O(nkt) ，n 是对象的个数，k 是簇的数目，t 是迭代的次数，通常 k ≪ n ，且 t ≪ n ，所以算法经常以局部最优结束。

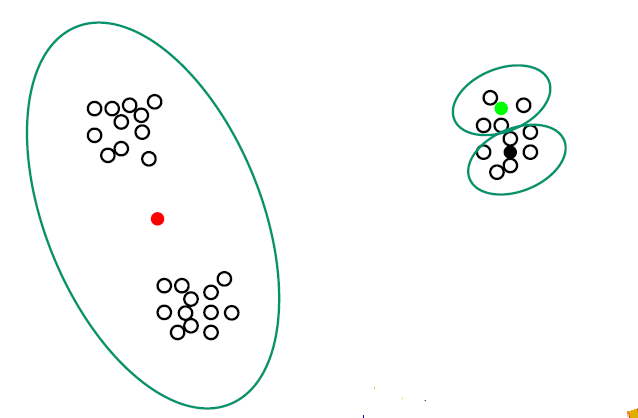
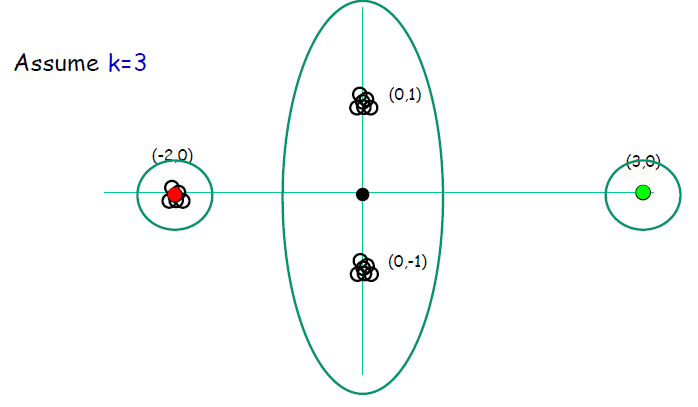
K-Means 的最大问题是要求先给出 k 的个数。k 的选择一般基于经验值和多次实验结果，对于不同的数据集，k 的取值没有可借鉴性。另外，K-Means 对孤立点数据是敏感的，少量噪声数据就能对平均值造成极大的影响。

The Lloyd’s Method

Input: n个数据点的集合 x¹, x², ⋯, xⁿ ∈ R^d

Initialize: 初始化簇中心 c₁, c₂, ⋯, c_k ∈ R^d 和簇 C₁, C₂, ⋯, C_k

Repeat: 直到满足停止条件

• For each j:C_j ← {x ∈ S, dist(x, c_j) < dist(x, c_i), i ≠ j, i = 1, 2, ⋯, k},保持 c₁, c₂, ⋯, c_k 不变，找出最优的簇 C₁, C₂, ⋯, C_k

• For each j: c_j ← mean   of   C_j 保持簇不变 C₁, C₂, ⋯, C_k 算出最优中心点 c₁, c₂, ⋯, c_k

每次迭代损失函数均在下降，并有下界，因此收敛。每次迭代 O(ndk) .

Lloyd方法初始化有多种方式，最常用的有以下几种:

• 从数据集中随机选取k个中心点
• Furthest Traversal
• k-means++

随机初始化

随机初始化过程如下图：

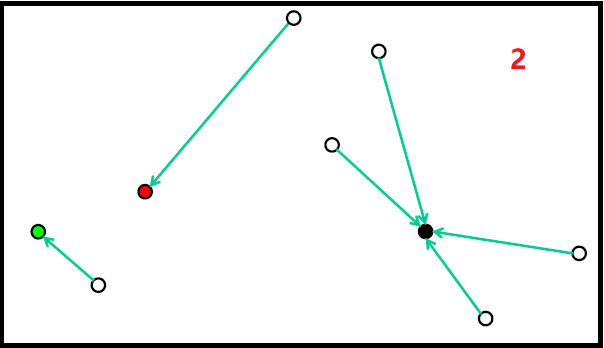
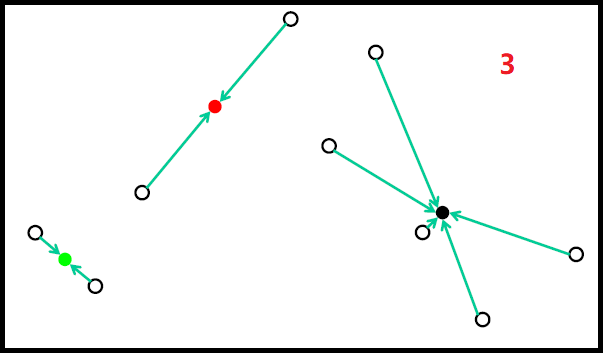
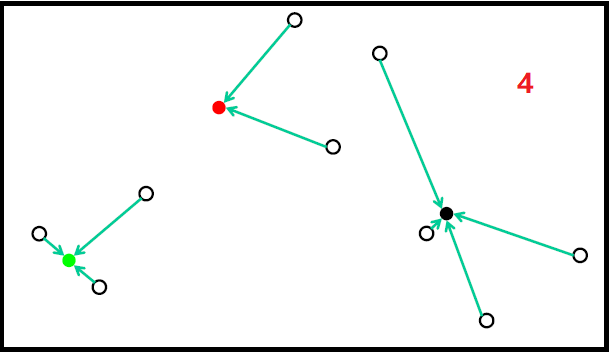
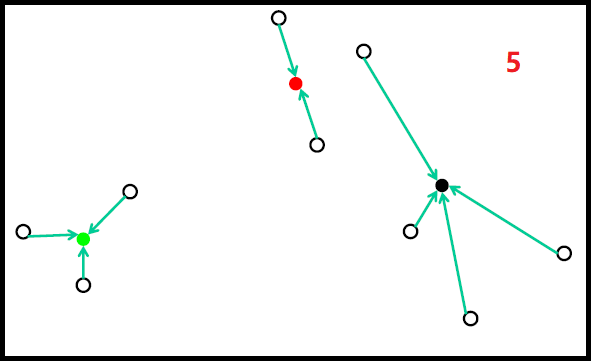
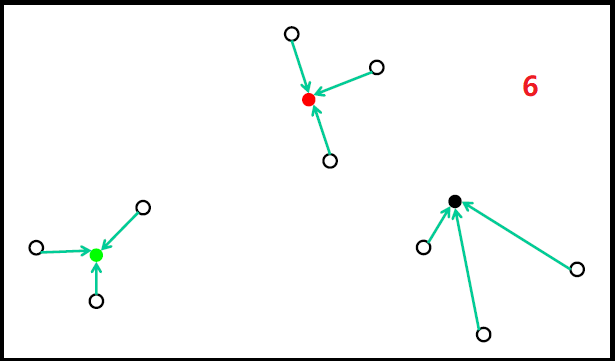
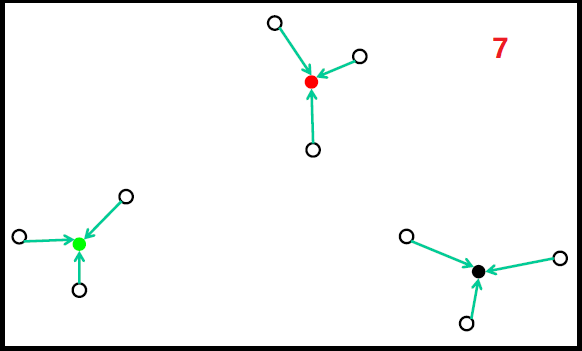
但随机初始化，会存在如下问题：

Furthest Traversal

首先任意选择一个簇的中心 c₁

For j = 1,2, ⋯ , k :

• 选择一个离已选择的中心点 c₁, c₂, ⋯, c_j − 1 都远的点 c_j 作为新的中心点

过程如下：

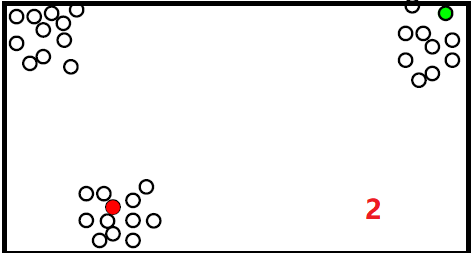
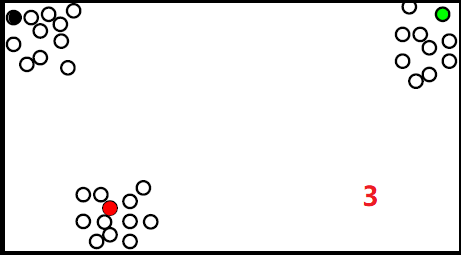
但是这种方法容易受到噪点的影响，如下：

k-means++

假设 D(x) 为点 x 到它最近中心点的距离

首先，随机选择 c₁

For j=2,…,k

• 在数据集中选择 c_j ，根据以下分布

Pr(c_j = xⁱ) ∝ min_{j^′ < j}∥xⁱ − c_j^′∥²

将上述距离平方算出后进行归一化，便是 xⁱ 被选为下一个中心点的概率，这样，离现有中心点越远则这个点被选择为下一个中心点的概率越高。

上述方法虽然噪点被选的概率很高，但是噪点的个数较少；而和现有中心点是不同簇的点同样离中心点较远，并且这样点的个数较多，因此这些点其中之一被选的概率应该比噪点被选中的概率高；这样可降低噪点对聚类结果的影响。

k-means++步骤

• 1.先从我们的数据库随机挑个随机点当“种子点”。

• 2.对于每个点，我们都计算其和最近的一个“种子点”的距离 D(x) 并保存在一个数组里，然后把这些距离加起来得到 Sum(D(x)) 。

• 3.然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在 Sum(D(x)) 中的随机值 Random ，然后用 Random− = D(x) ，直到 Random <  = 0 ，此时的点就是下一个“种子点”。

• 4.重复第（2）和第（3）步直到所有的K个种子点都被选出来。

• 5.进行K-Means算法。

k-means++ 每次需要计算点到中心的距离，复杂度为 O(ndk) , d维。

可以看到算法的第三步选取新中心的方法，这样就能保证距离 D(x) 较大的点，会被选出来作为聚类中心了。至于为什么原因很简单，如下图 所示：

假设A、B、C、D的 D(x) 如上图所示，当算法取值 Sum(D(x)) * Random 时，该值会以较大的概率落入 D(x) 较大的区间内，所以对应的点会以较大的概率被选中作为新的聚类中心。

可以将上述方法进行推广

Pr(c_j = xⁱ) ∝ min_{j^′ < j}∥xⁱ − c_j^′∥^α

当 α = 0 时就是随机初始化

当 α = ∞ 时就是 Furthest Traversal

当 α = 2 时就是k-means++

当 α = 1 时就是k-median

4.2 学习向量化

与 k 均值算法类似，学习向量化(Learning Vector Quantization, LVQ)也是试图找到一组原型向量来刻画聚类结构，但与一般聚类算法不同的是，LVQ假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。

给定样本集

D = {(x₁, y₁), (x₂, y₂), ⋯, (x_m, y_m)}

每个样本 x_j 是由 n 个属性描述的特征向量 (x_j1; x_j2, ⋯, x_jn), y_j ∈ 𝒴 是样本 x_j 的类别标记。LVQ的目标是学得一组 n 维原型向量

{p₁, p₂, ⋯, p_q}

每个原型向量代表一个聚类簇，簇标记 t_i ∈ 𝒴 ,学习率参数 η ∈ (0, 1)

算法主要步骤包括：初始化原型向量；迭代优化，更新原型向量。

具体来说，主要是：

• 1.对原型向量初始化，对第 q 个簇可从类别标记为 t_q 的样本中随机选取一个作为原型向量，这样初始化一组原型向量

{p₁, p₂, ⋯, p_q}

• 2.从样本中随机选择样本 (x_j, y_j) ,计算样本 x_j 与 p_i(0 ≤ i ≤ q) 的距离：d_ji = ∥x_j − p_i∥₂;找出与 x_j 距离最近的原型向量p_i^*, i^* = arg min_{i ∈ {1, 2, ⋯, q}}d_ji$

• 3.如果y_j = t_i^*则令p_i^′ = p_i^* + η ⋅ (x_j − p_i^*),否则令p_i^′ = p_i^* − η ⋅ (x_j − p_i^*)

• 4.更新原型向量,p_i^* = p_i^′

• 5.判断是否达到最大迭代次数或者原型向量更新幅度小于某个阈值。如果是，则停止迭代，输出原型向量；否则，转至步骤2。

LVQ的关键是第3-4步，即如何更新原型向量。对样本 x_j ,若原型向量p_i^*与 x_j 的标记相同，则令p_i^*向 x_j 的方向靠拢，此时新的原型向量为

p_i^′ = p_i^* + η ⋅ (x_j − p_i^*)

p_i^′ 与 x_j 之间的距离为

∥p_i^′ − x_j∥₂ = ∥p_i^* + η ⋅ (x_j − p_i^*) − x_j∥₂ = (1 − η)⋅∥p_i^* − x_j∥₂

则原型向量p_i^*在更新为 p_i^′ 之后将更接近 x_j .

类似的，若p_i^*与 x_j 的标记不同，则更新后的原型向量与 x_j 之间的距离将增大为(1 + η)⋅∥p_i^* − x_j∥₂,从而更远离 x_j .

在学得一组原型向量{p₁, p₂, ⋯, p_q}后，即可实现对样本空间 𝒳 的簇划分。每个原型向量 p_i 定义了与之相关的一个区域 R_i ,该区域中每个样本与 p_i 的距离不大于它与其他原型向量 p_i^′(i^′ ≠ i) 的距离，即

R_i = {x|∥x − p_i∥₂ ≤ ∥x − p_i^′∥₂, i^′ ≠ i}

由此形成了对样本空间 𝒳 的簇划分{R₁, R₂, ⋯, R_q},该划分通常称为Voronoi剖分（Voronoi tessellation）.

4.3 高斯混合聚类

与 k 均值，LVQ用原型向量来刻画聚类结构不同，高斯混合(Mixture-of-Gaussian)聚类采用概率模型来表达聚类原型，

对 n 维样本空间 𝒳 中的随机向量 x ,若 x 服从高斯分布，其概率密度为

其中 μ 是 n 维均值向量， Σ 是 n × n 的协方差矩阵。 高斯分布完全由均值向量 μ 和协方差矩阵 Σ 这两个参数确定。为了显示高斯分布与相应参数的依赖关系，将概率密度函数记为

p(x|μ, Σ)

定义高斯混合分布

该分布共由 k 个混合成分组成，每个混合成分对应一个高斯分布，其中 μ_i, Σ_i 是第 i 个高斯混合成分的参数，而 α_i > 0 为相应的混合系数(mixture coefficient), .

假设样本的生成过程由高斯混合分布给出：首先，根据 α₁, α₂, ⋯, α_k 定义的先验分布选择高斯混合成分，其中 α_i 为选择第i 个混合成分的概率；然后，根据被选择的混合成分的概率进行采样，从而生成相应的样本。

常用EM算法对上述分布进行迭代优化求解，之前已详细讨论过EM算法，此处不再进行讨论。

5.密度聚类

密度聚类亦称基于密度的聚类(density-based clustering),此类算法假设聚类结构能通过样本分布的紧密程度确定。通常情形下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。

DBSCAN是一种著名的密度聚类算法，它基于一组邻域(neighborhood)参数 (ϵ, MinPts) 来刻画样本分布的紧密程度。给定数据集D = {x₁, x₂, ⋯, x_m},定义下面这几个概念：

• ϵ− 邻域：对 x_j ∈ D ，其 ϵ− 邻域包含样本集 D 中与 x_j 的距离不大于 ϵ 的样本，即N_ϵ(x_j) = {x_iinD| dist(x_i, x_j) ≤ ϵ}。

• 核心对象(core object): 若 x_j 的 ϵ− 邻域至少包含 MinPts 个样本，即|N_ϵ(x_j)| ≥ MinPts,则 x_j 是一个核心对象；

• 密度直达(directly density-reachable)：若 x_j 位于 x_i 的 ϵ− 邻域中，且 x_i 是核心对象，则称 x_j 由 x_i 密度直达；

• 密度可达(density-reachable)：对 x_i 与 x_j ,若存在样本序列 p₁, p₂, ⋯, p_n ,其中 p₁ = x_i, p_n = x_j 且 p_i + 1 由 p_i 密度直达，则称 x_j 由 x_i 密度可达；

• 密度相连(density-connected)：对 x_i 与 x_j ,若存在 x_k 使得 x_i 与 x_j 均由 x_k 密度可达，则称 x_i 与 x_j 密度相连。

下图给出上述概念的直观概念

上图中 MinPts = 3 ，虚线显示出 ϵ− 邻域, x₁ 是核心对象， x₂ 由 x₁ 密度直达， x₃ 由 x₁ 密度可达，x₃ 与 x₄ 密度相连。

基于这些概念，DBSCAN将簇定义为：由密度可达关https://zhuanlan.zhihu.com/p/577060385系导出的最大的密度相连样本集合。形式化地说，给定邻域参数 (ϵ, MinPts) ，簇 C ⊆ D 是满足以下性质的非空样本子集:

• 连接性(connectivity)： x_i ∈ C, x_j ∈ C ⇒ x_i 与 x_j 密度相连

• 最大性(maximality): x_i ∈ C, x_j 由 mathbfx_i 密度可达  ⇒ x_j ∈ C

若 x 为核心对象，由 x 密度可达的所有样本组成的集合记为X = {x^′ ∈ D|x^′   density − reachable   by   x},则不难证明 X 即为满足连接性与最大性的簇。

于是，DBSCAN算法先任选数据集中的一个核心对象为种子(seed),再由此出发确定相应的聚类簇，算法描述如下。算法先根据给定的邻域参数 (ϵ, MinPts) 找出核心对象；然后以任一核心对象为出发点，找出其密度可达的样本生成聚类簇，直到所有核心对象均被访问为止。

输入：样本集D = {x₁, x₂, ⋯, x_m},邻域参数 (ϵ, MinPts) ,样本距离度量方式

输出：簇划分

1. 初始化核心对象集合 Ω = ∅ ,初始化聚类簇数 k = 0 ，初始化未访问样本集合 Γ = D ，簇划分 C = ∅

2. 对于 j = 1, 2, ⋯, m 按下面的步骤找出所有的核心对象：

• 1. 通过距离度量方式，找到样本 x_j 的 ϵ− 邻域子样本集 N_ϵ(x_j)
• 2. 如果子样本集样本个数满足|N_ϵ(x_j)| ≥ MinPts,将样本 x_j 加入核心对象样本集合:Ω = Ω ∪ {x_j}

3. 如果核心对象集合 Ω = ∅ ，则算法结束，否则转入步骤4

4. 在核心对象集合 Ω 中，随机选择一个核心对象 o ,初始化当前簇核心对象队列Ω_cur = {o},初始化类别序号 k = k + 1 ,当初始化当前簇样本集合C_k = {o},更新未访问样本集合Γ = Γ − {o}

5. 如果当前簇核心对象队列 Ω_cur = ∅ ，则当前聚类簇 C_k 生成完毕。更新簇划分C = {C₁, C₂, ⋯, C_k},更新核心对象集合 Ω = Ω − C_k ,转入步骤3.

6. 在当前簇核心对象队列 Ω_cur 中取出一个核心对象 o^′ ,通过邻域距离阈值 ϵ 找出所有的 ϵ− 邻域子集样本 N_ϵ(o^′) ,令 Δ = N_ϵ(o^′) ∩ Γ ,更新当前簇样本集合 C_k = C_k ∪ Δ ,更新未访问样本集合 Γ = Γ − Δ ,更新 Ω_cur = Ω_cur ∩ (N_ϵ(o^′) ∩ Ω) ,转入步骤5.

5.1 DBSCAN小结

对于那些异常样本点或者说少量游离于簇外的样本点，这些点不在任何一个核心对象在周围，在DBSCAN中一般将这些样本点标记为噪音点。

在DBSCAN中，一般采用最近邻思想，采用某一种距离度量来衡量样本距离，比如欧式距离。对应少量的样本，寻找最近邻可以直接去计算所有样本的距离，如果样本量较大，则一般采用KD树或者球树来快速的搜索最近邻。

某些样本可能到两个核心对象的距离都小于 ϵ ，但是这两个核心对象由于不是密度直达，又不属于同一个聚类簇，此时DBSCAN采用先来后到，先进行聚类的类别簇会标记这个样本为它的类别。也就是说BDSCAN的算法不是完全稳定的算法。

DBSCAN的主要优点有：

1. 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

2. 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

3. 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

1. 如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

2. 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

3. 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值 ϵ ，邻域样本数阈值 MinPts 联合调参，不同的参数组合对最后的聚类效果有较大影响。

6.层次聚类

层次聚类(hierarchical clustering)试图在不同层次对数据集进行划分，从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略，也可采用“自顶向下”的分拆策略。

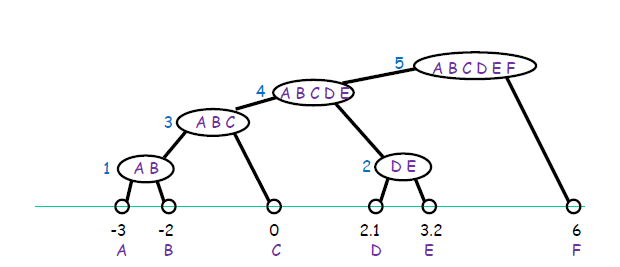
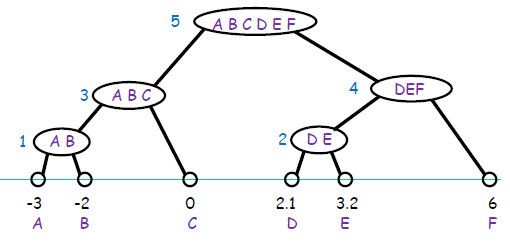
AGNES是一种采用自底向上聚合策略的层次聚类算法。它将数据集中的每个样本看做一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直到达到预设的聚类个数。这里的关键是如何计算聚类簇之间的距离。实际上，每一个簇是一个样本集合，因此，值需要采用关于集合的某种距离即可。例如，给定聚类簇 C_i 与 C_j ，可通过下面的式子来计算距离：

• 最小距离：d_min(C_i, C_j) = min_{x ∈ Ci, z ∈ Cj}dist(x, z)

• 最大距离：d_max(C_i, C_j) = max_{x ∈ Ci, z ∈ Cj}dist(x, z)

• 平均距离：

显然，最小距离由两个簇的最近样本决定，最大距离由两个簇的最远样本决定，而平均距离则由两个簇的所有样本共同决定。当聚类簇聚类由 d_min, d_max, d_avg 计算时，AGNES算法相应地称为单链接(Single-linekage),全链接(Complete-linkage),均链接(Average-linkage)算法。

单链接步骤如下图（1-5）

全链接步骤如下图（1-5）

AGNES算法描述如下：

输入样本集D = {x₁, x₂, ⋯, x_m},聚类距离度量函数 d ；聚类簇数 k;

1. 将每个对象当做一个簇进行初始化，C_j = {x_j}, j = 1, 2, ⋯, m

2. 设置当前聚类簇数 q = m

3. 计算每两个簇的距离，得到距离矩阵 M, M(i, j) = M(j, j) = d(C_i, C_j)

4. 当 q > k 时，找出距离最近的两个聚类簇C_i^*, C_j^*,合并C_i^*, C_j^*:C_i^* = C_i^*⋃C_j^*;对于j = j^* + 1, j^* + 2, ⋯, q的聚类簇 C_j 重编号为 C_j − 1;然后删除距离矩阵 M 的第j^*行和列；对于 j = 1, 2, ⋯, q − 1 ,计算M(i^*, j); 更新 q = q − 1 ，直到达到预设的聚类簇数。

输出：划分C = {C₁, C₂, ⋯, C_k}

AGNES算法简单，但遇到合并点选择困难的情况.一旦一组对象被合并，不能撤销,算法的复杂度为 O(n²) ，不适合大数据集计算.

DIANA算法

DIANA（Divisive Analysis）算法属于分裂的层次聚类，首先将所有的对象初始化到一个簇中，然后根据一些原则（比如最邻近的最大欧式距离），将该簇分类。直到到达用户指定的簇数目或者两个簇之间的距离超过了某个阈值。

DIANA用到如下两个定义：

1. 簇的直径：在一个簇中的任意两个数据点都有一个欧氏距离，这些距离中的最大值是簇的直径

2. 平均相异度（平均距离）

算法描述：

输入：包含 n 个对象的数据库，终止条件簇的数目k

输出：k 个簇，达到终止条件规定簇数目

1. 将所有对象整个当成一个初始簇

2. 在所有簇中挑选出具有最大直径的簇；找出所挑出簇里与其他点平均相异度最大的一个点放入splinter group，剩余的放入old party中。

3. 在old party里找出到splinter group中点的最近距离不大于old party中点的最近距离的点，并将该点加入splinter group

4. 重复 3 直到没有新的old party的点被分配给splinter group；

5. Splinter group 和old party为被选中的簇分裂成的两个簇，与其他簇一起组成新的簇集合

算法性能：

缺点是已做的分裂操作不能撤销，类之间不能交换对象。如果在某步没有选择好分裂点，可能会导致低质量的聚类结果。大数据集不太适用。

参考

1. 周志华 《机器学习》