LLM(十一)——Mamba

一、SSM(State Space Model)

1.1 State Space

下图中每个小框代表迷宫中的一个位置，并有某些隐式的信息，例如你距离出口有多远:

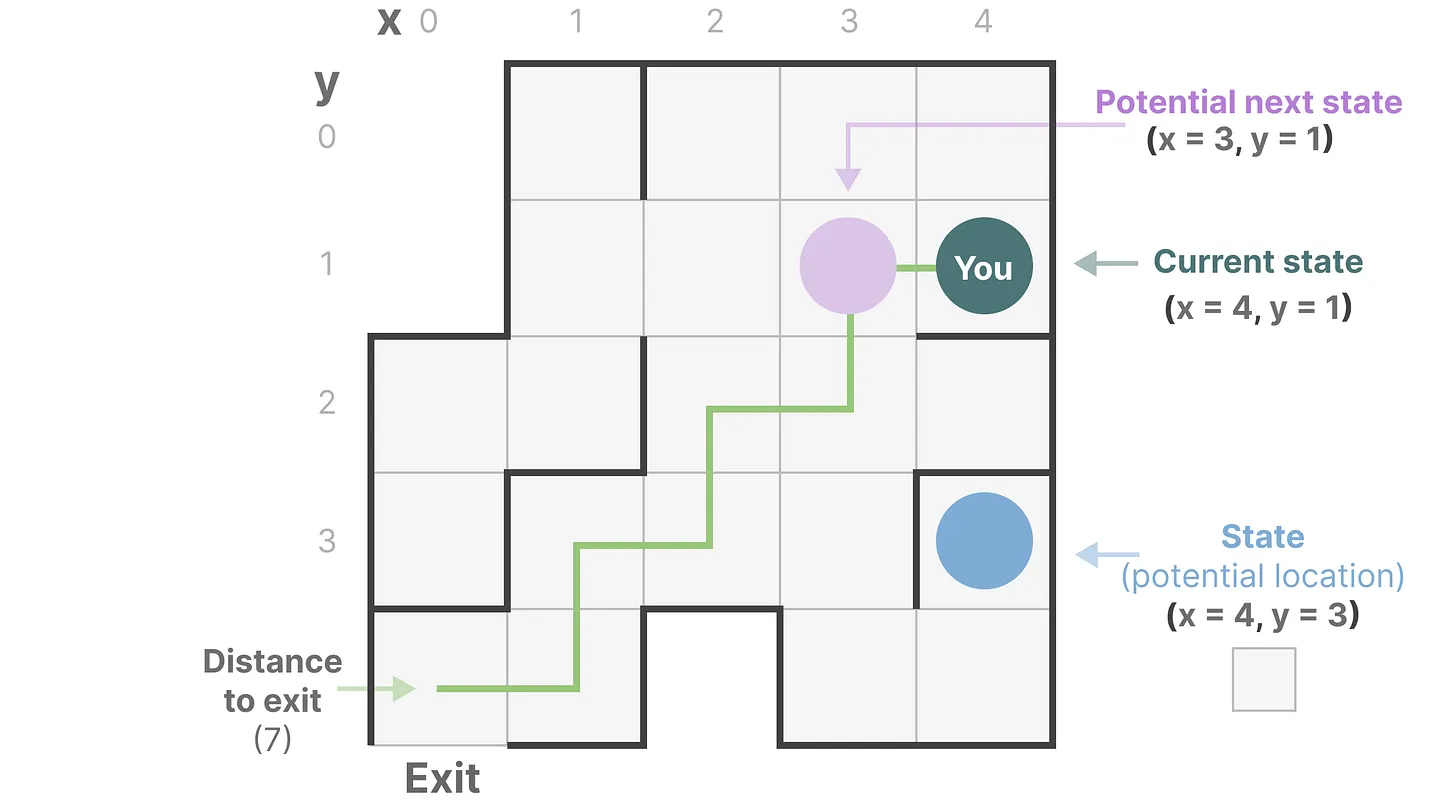
而上述迷宫可以简化建模为一个“状态空间表示state space representation”，每一个小框显示:

当前所在位置（当前状态Current State）
下一步可以前往哪里(未来可能的状态Possible Future States)
以及哪些变化会将你带到下一个状态(向右或向左)

而描述状态的变量(在上述示例中为 X 和 Y 坐标以及到出口的距离)可以表示为“状态向量state vectors”。

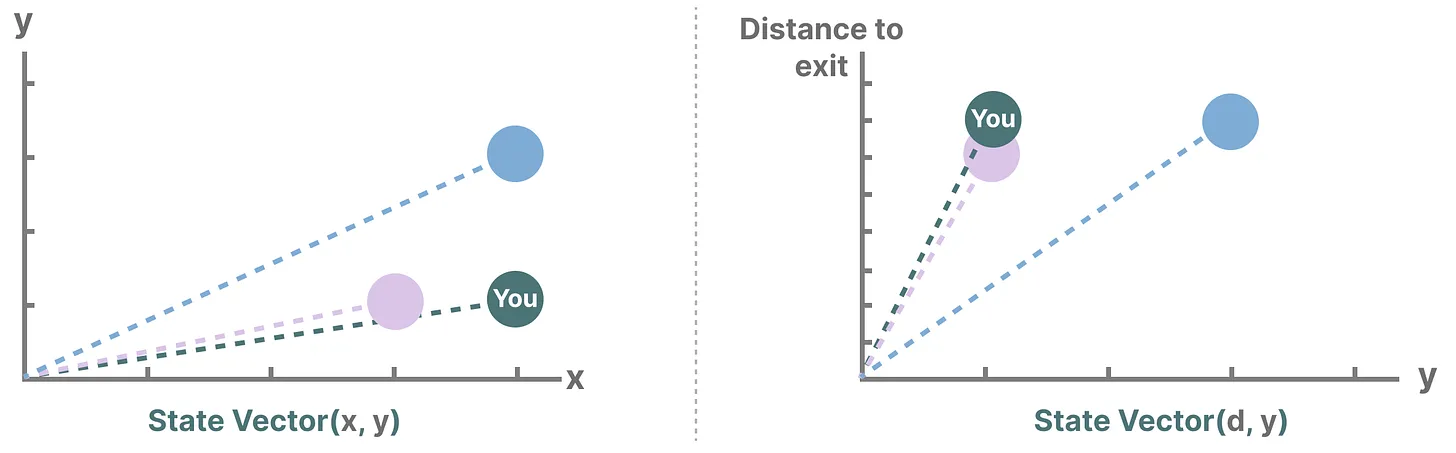
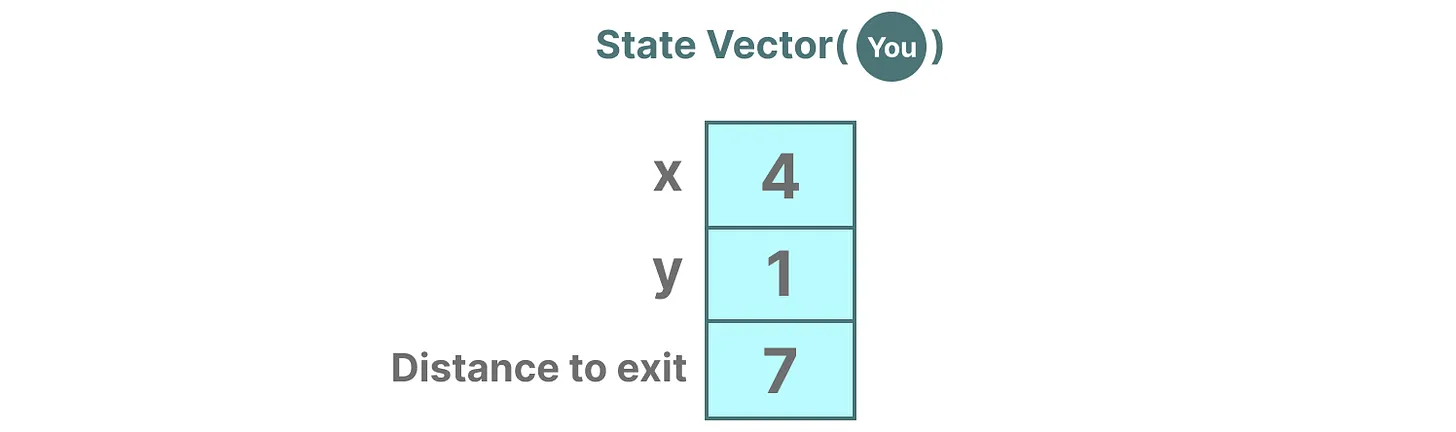
在语言模型中的嵌入或向量也经常用于描述输入序列的“状态”。例如，当前位置的向量（状态向量）可能看起来有点像这样：

1.2 SSM

SSM 是用于描述状态表示并根据某些输入预测其下一个状态可能是什么的模型，在t时刻，SSMs可描述为：

映射输入序列x(t)，比如在迷宫中向左和向下移动
到潜在状态表示h(t)，比如距离出口距离和 x/y 坐标
并导出预测输出序列y(t)，比如再次向左移动以更快到达出口

然而，SSM不使用离散序列（如向左移动一次），而是将连续序列作为输入并预测输出序列。

SSM 假设动态系统（例如在 3D 空间中移动的物体）可以通过两个方程从其在时间t时的状态进行预测。

RNN的循环结构: h(t) = tanh (Wh_t − 1 + Ux_t)和上面的第一个方程非常类似，都是通过上一个隐藏状态和当前输入综合得到当前的隐藏状态，只是两个权重W, U换成了A, B两个系数，且去掉了非线性的激活函数tanh 。
A就是存储着之前所有历史信息的浓缩精华(可以通过一系列系数组成的矩阵表示之)，以基于A更新下一个时刻的空间状态hidden state

通过求解这些方程，假设可以揭示统计原理，以根据观察到的数据（输入序列和先前状态）预测系统的状态。

1.2.1 状态方程与输出方程

SSM的目标是找到状态表示h(t)，以便结合其与输入序列预测输出序列。

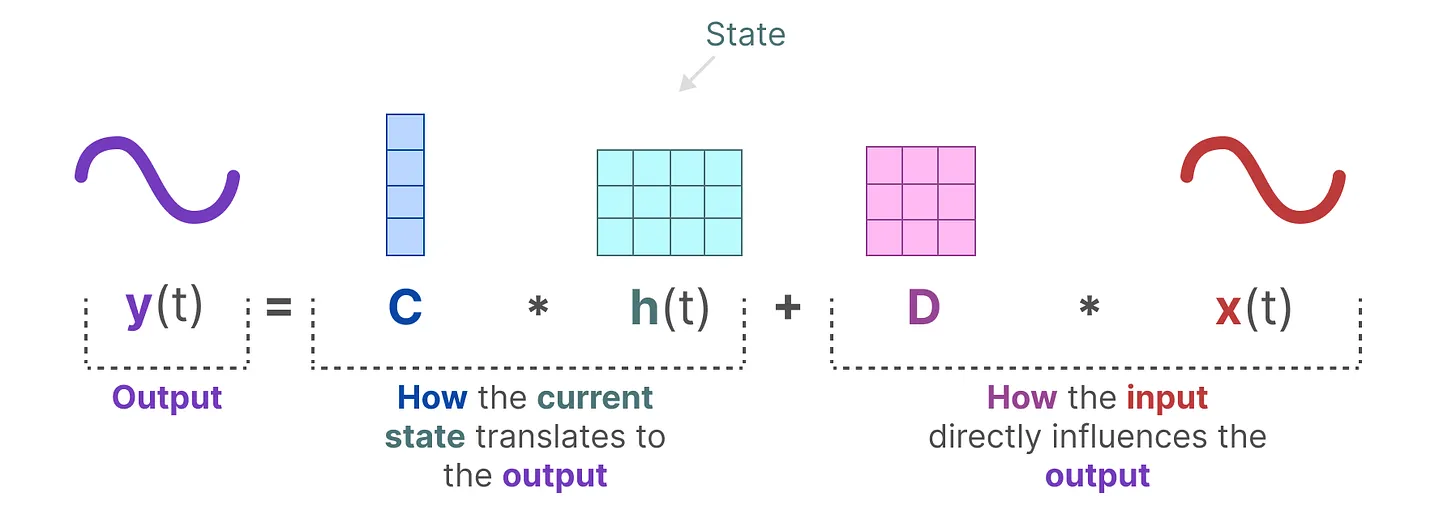
这两个方程是SSM的核心。矩阵A, B, C, D是可学习的,此处的四个矩阵在不同的输入之下是固定不变的，后续的改进版本mamba中则这4个矩阵都是随着输入不同而可变的参数。

状态方程

矩阵B与输入x(t)相乘之后，再加上矩阵A与前一个状态h(t)相乘的结果。

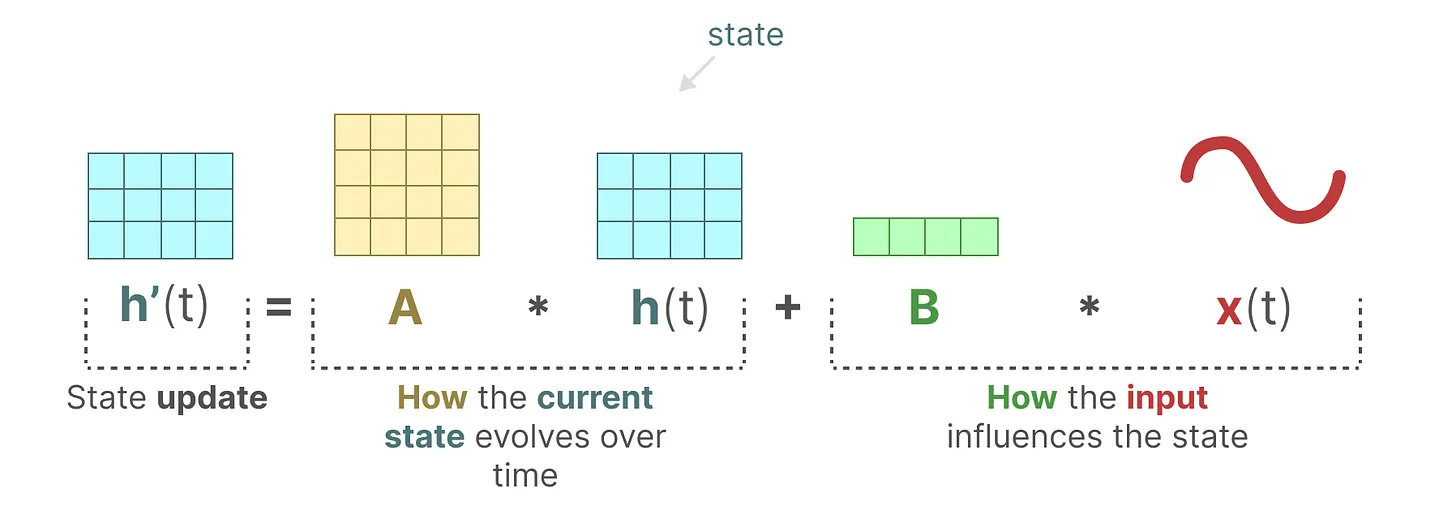
换言之，B矩阵影响输入x(t)，A矩阵影响前一个状态h(t)，而h(t)指的是任何给定时间t的潜在状态表示(latent state representation)，而x(t)指的是某个输入。表示成这样更好：h(t) = Ah(t − 1) + Bx(t)。

输出方程

描述了状态如何转换为输出(通过矩阵C)，以及输入如何影响输出(通过矩阵D)

1.2.2 SSM架构

上述两个方程可以统一成以下架构：

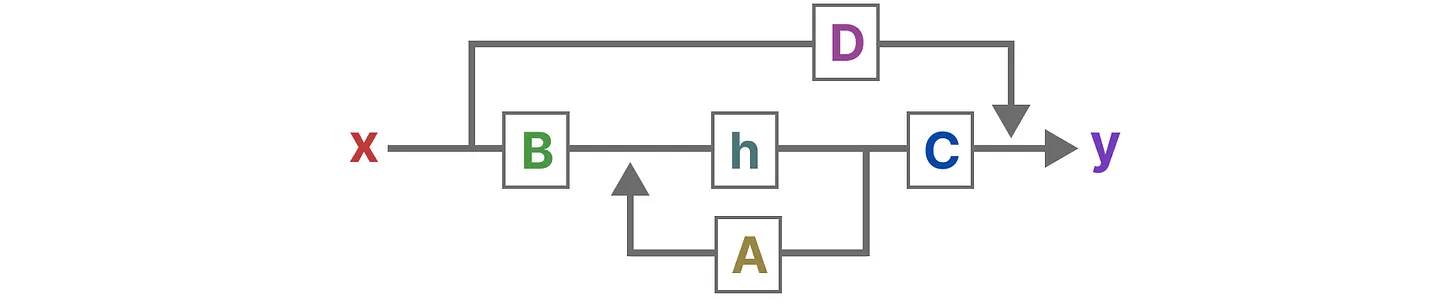
下面通过逐步拆解，以了解这些矩阵如何影响学习过程。

假设我们有一些输入信号x(t)，该信号首先乘以矩阵B

上面第一步的结果，加上上一个状态与矩阵A相乘(矩阵A描述了所有内部状态如何连接)的结果，用来更新状态state

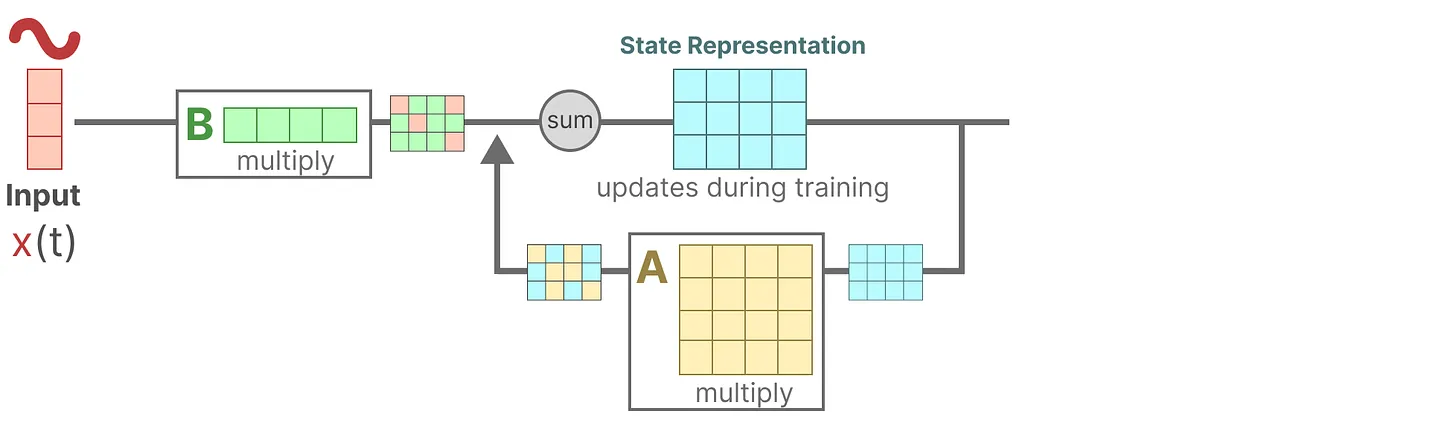
然后，使用矩阵C来将状态转换为输出

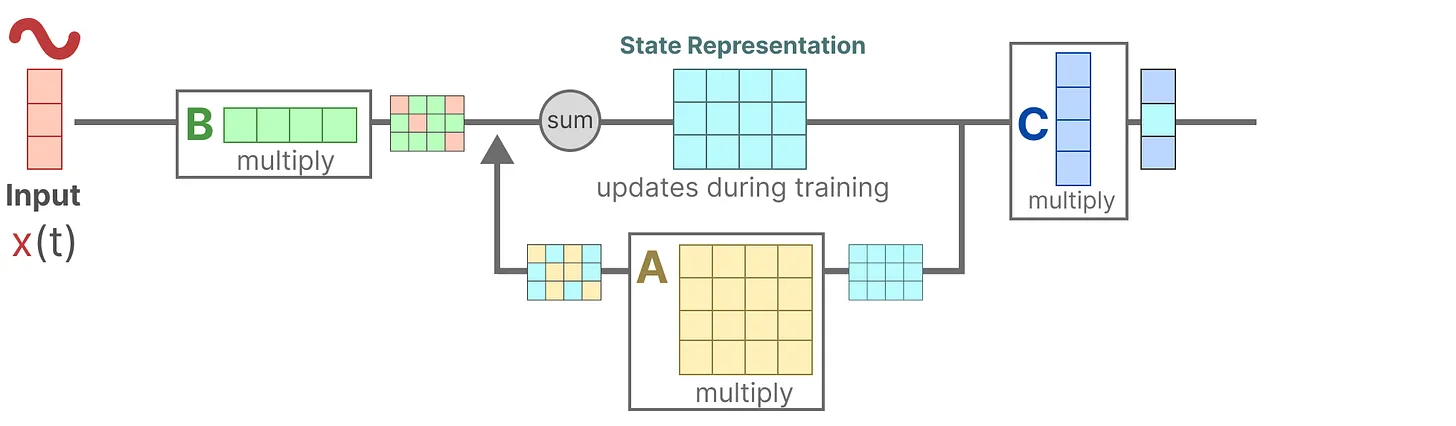
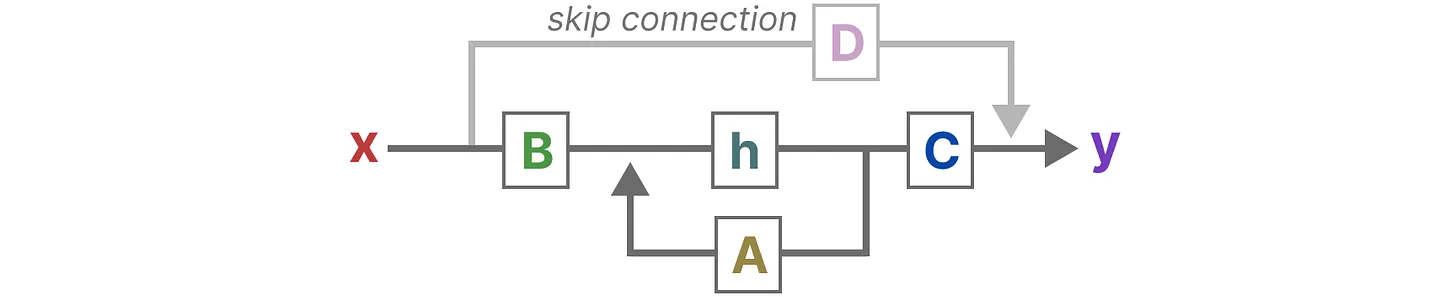
最后，再利用矩阵D提供从输入到输出的直接信号，这通常也称为跳跃连接skip-connection

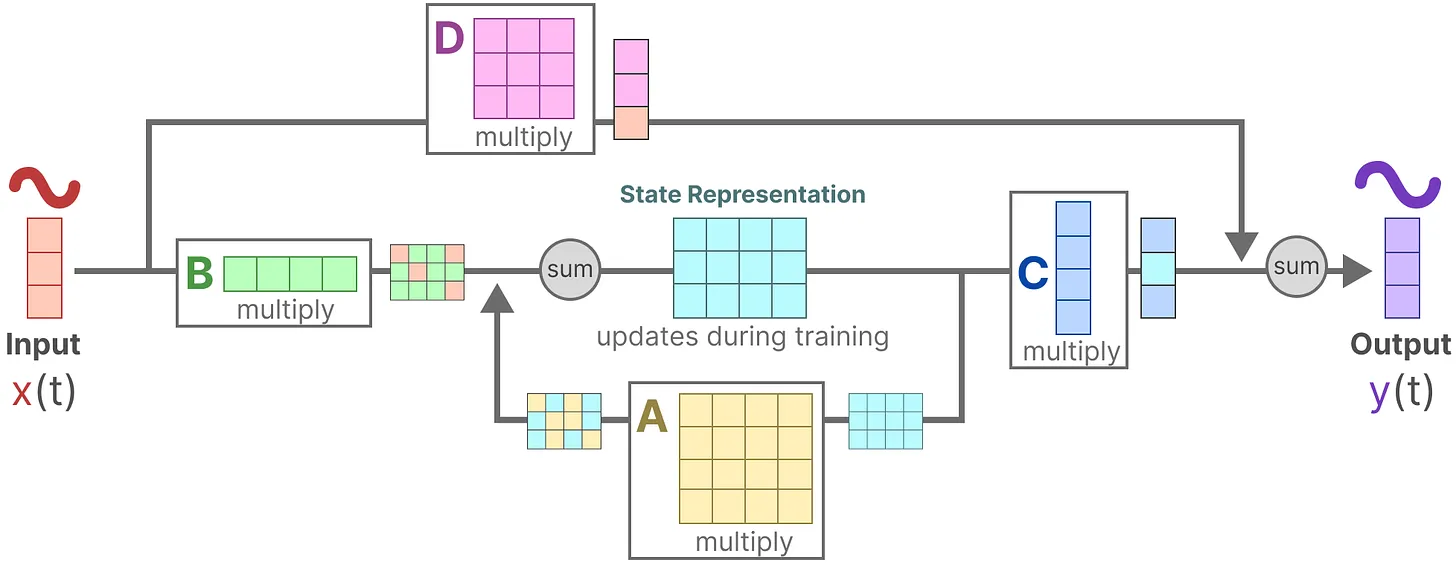
由于矩阵D类似于跳跃连接，因此在没有跳跃连接的情况下，SSM 通常被视为如下

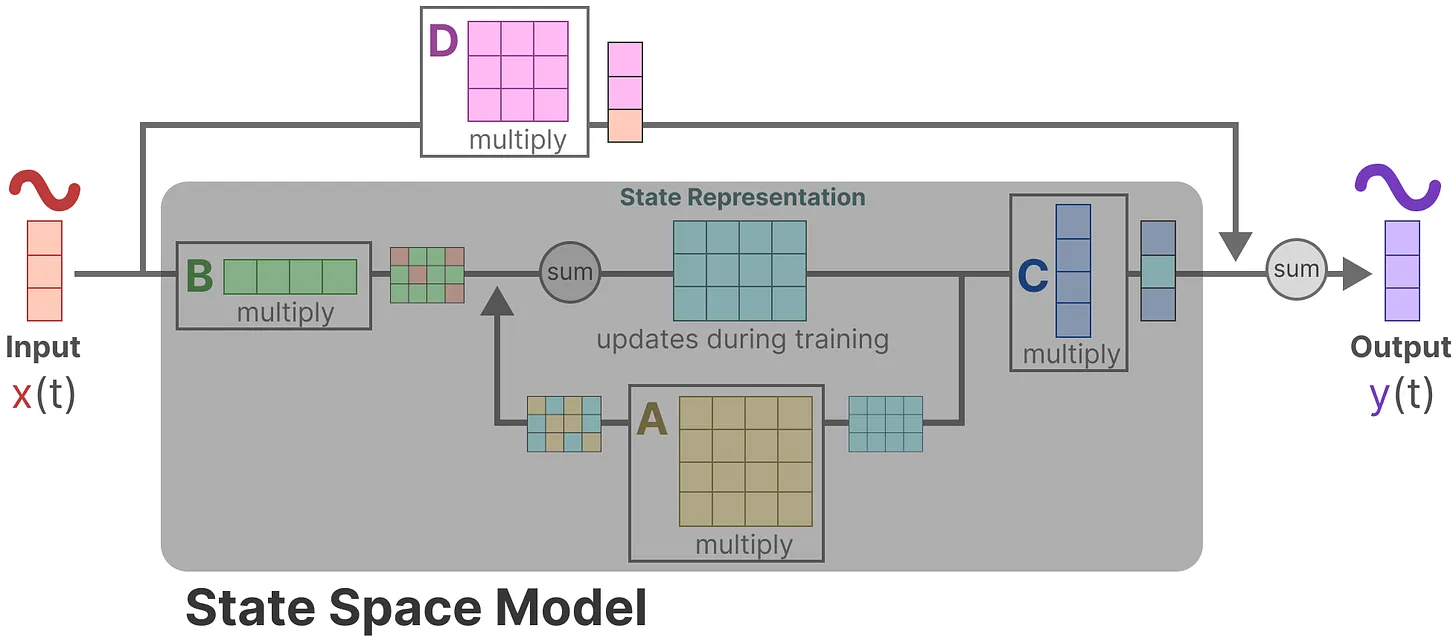
回到简化视角，现在可以关注只矩阵A, B, C构建的SSM核心

这两个方程共同旨在根据观测数据预测系统的状态，且考虑到输入一般都是连续的，因此SSM的主要表示是连续时间表示( continuous-time representation )。

1.3 从SSM到S4

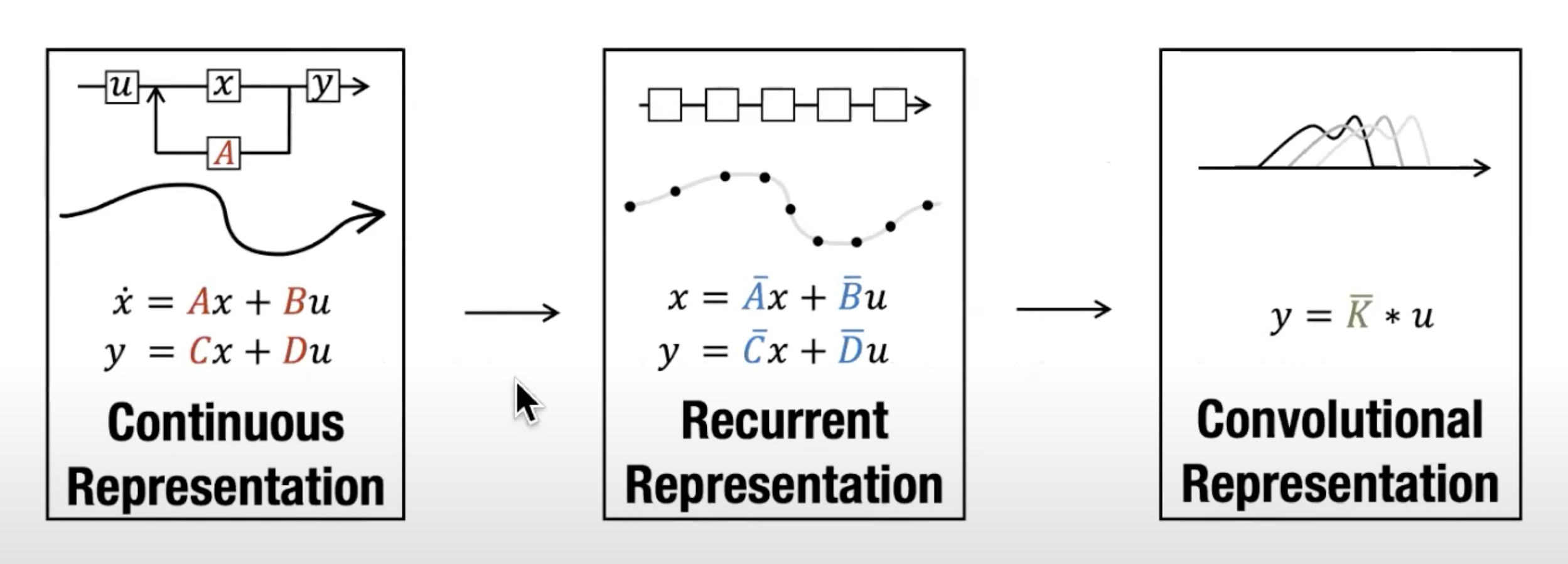
1.3.1 从连续到离散

由于除了连续的输入之外，还会通常碰到离散的输入(如文本序列)，不过，就算SSM在离散数据上训练，它仍能学习到底层蕴含的连续信息，因为在SSM眼里，sequence不过是连续信号signal的采样，或者说连续的信号模型是离散的序列模型的概括。

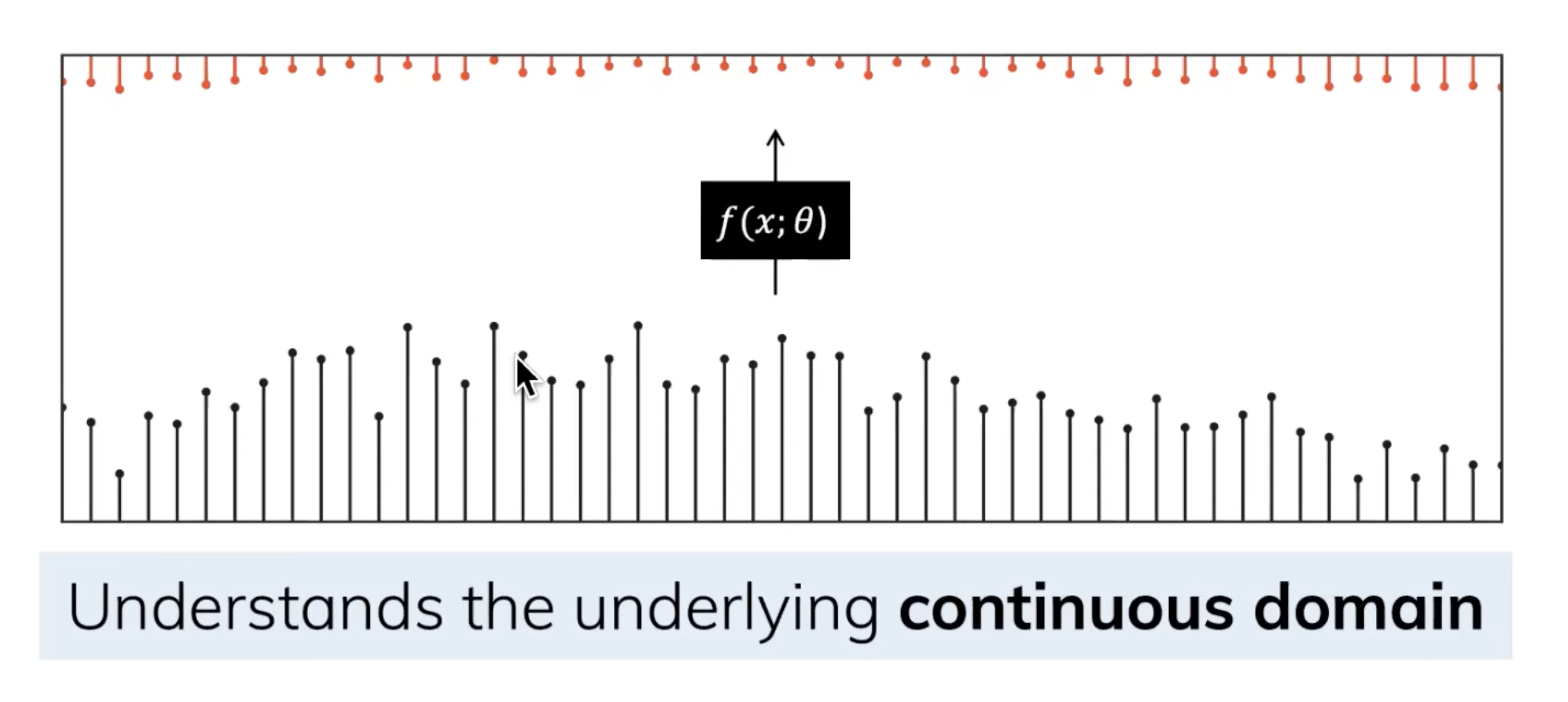
利用零阶保持技术(Zero-order hold technique)处理离散化数据。

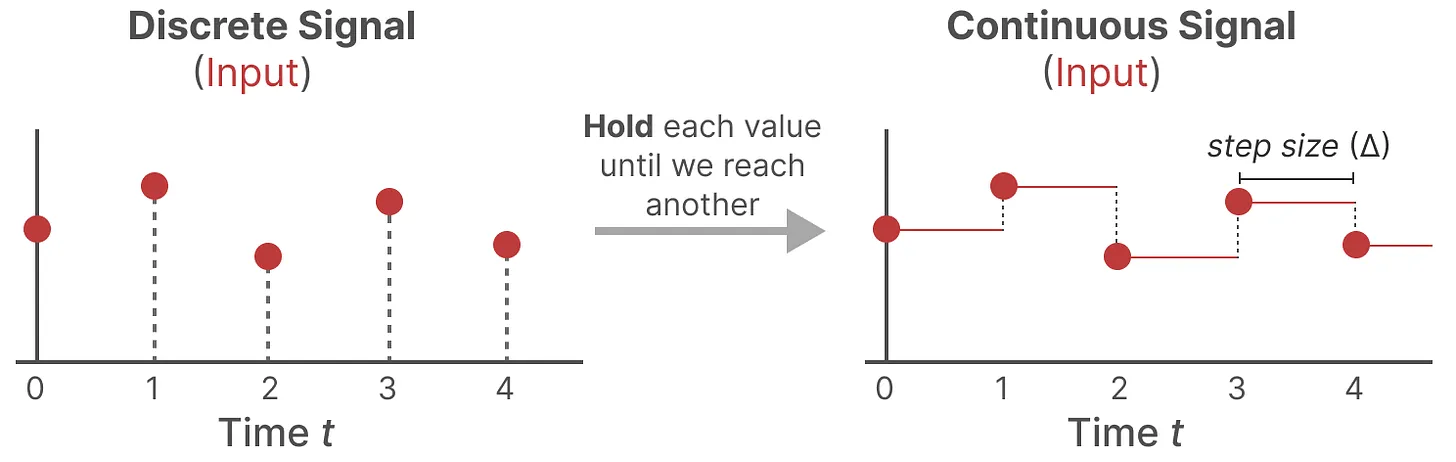
首先，每次收到离散信号时，都会保留其值，直到收到新的离散信号。此过程会创建 SSM 可以使用的连续信号
保持该值的时间由一个新的可学习参数表示，称为步长Δ，它代表输入的阶段性保持(resolution)
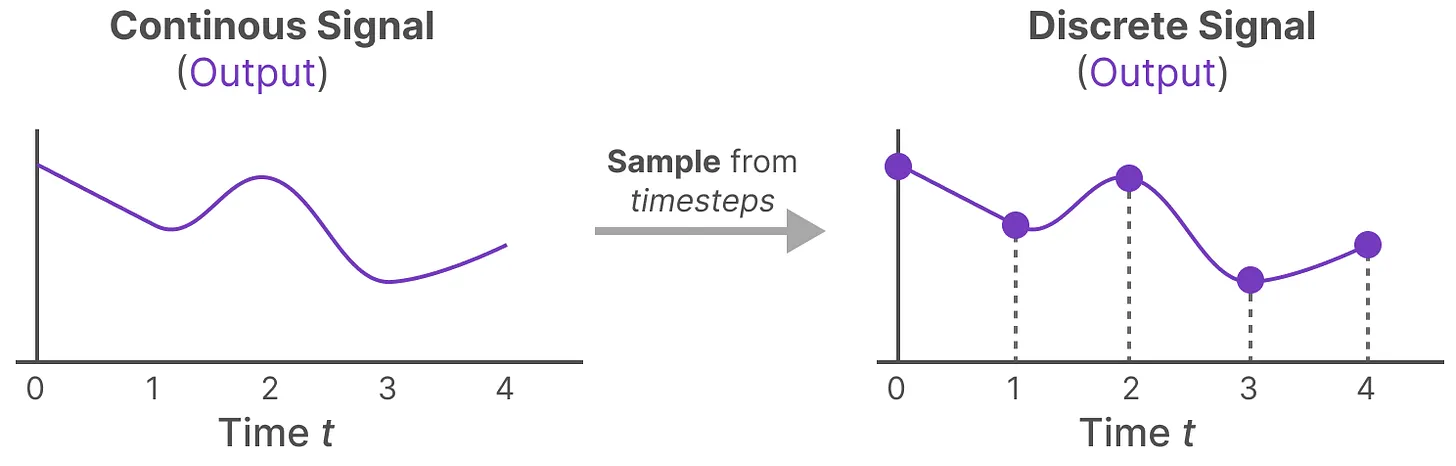
有了连续的输入信号后，便可以生成连续的输出，并且仅根据输入的时间步长对值进行采样

最终够从连续 SSM 转变为离散SSM，使得不再是函数到函数x(t) → y(t)，而是序列到序列x_k → y_k，所以你看到，矩阵Ā和B̄现在表示模型的离散参数，且这里使用k，而不是t来表示离散的时间步长

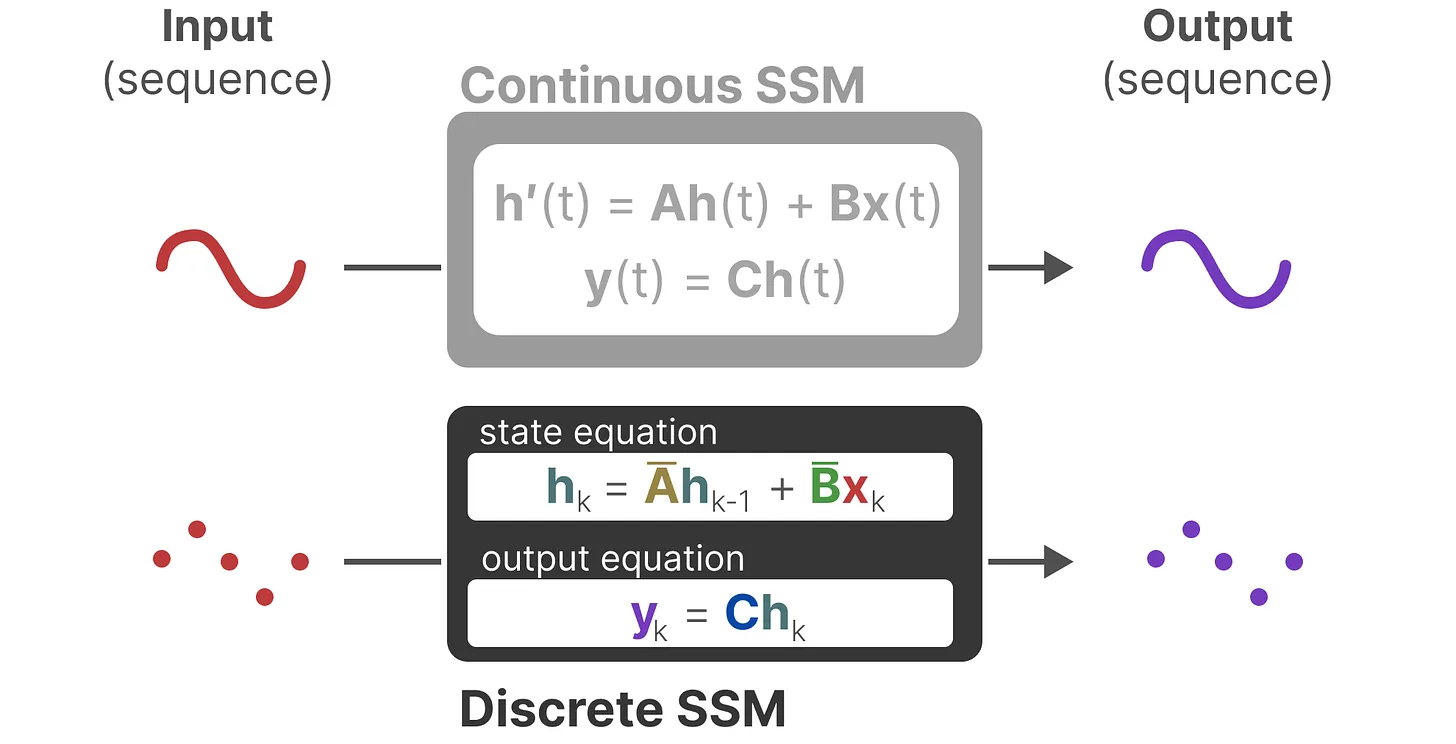
在保存时，仍然保存矩阵A的连续形式(而非离散化版本)，只是在训练过程中，连续表示被离散化(During training, the continuous representation is discretized)

1.3.2 循环结构表示：方便快速推理

总之，离散 SSM 允许可以用离散时间步长重新表述问题

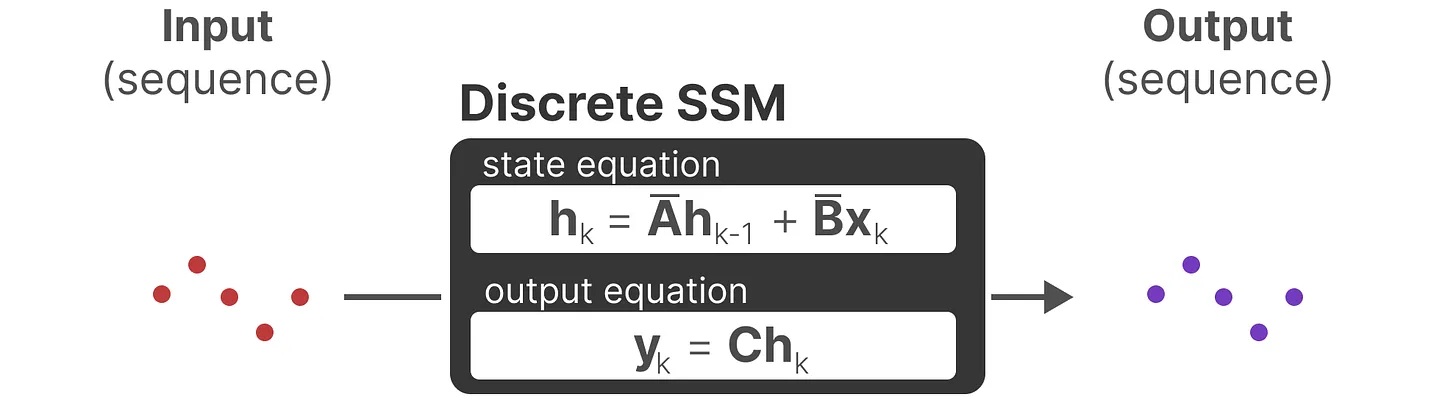
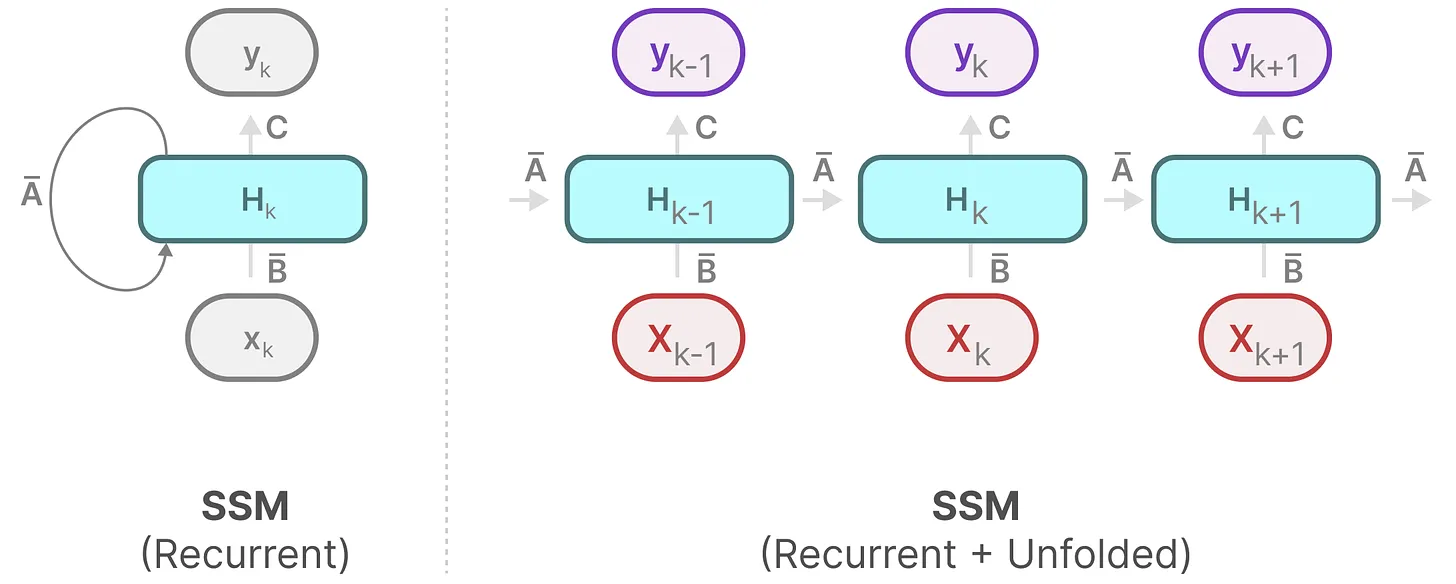
在每个时间步，都会涉及到隐藏状态的更新(比如h_k取决于B̄x_k和Āh_k − 1的共同作用结果，然后通过Ch_k预测输出y_k)

展开一下y₂s

如此，便可以用RNN的结构来处理

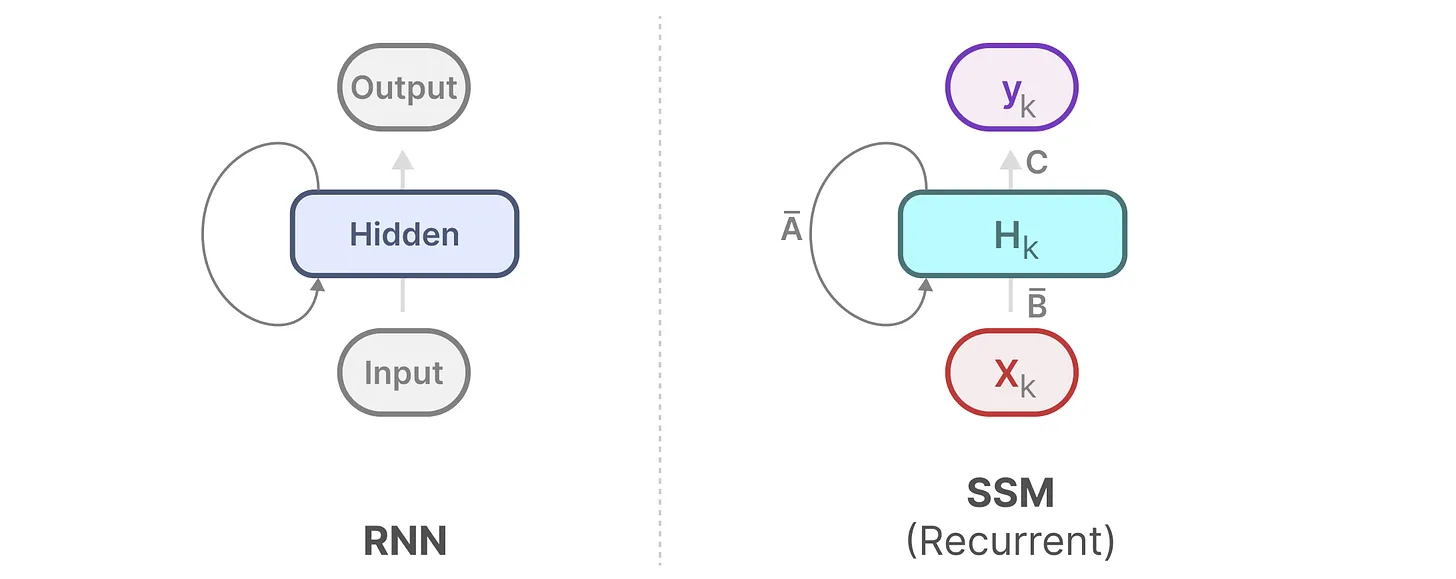
然后可以这样展开(其中，h_k始终是B̄x_k和Āh_k − 1的共同作用之下更新的)

1.3.3 卷积结构表示：方便并行训练

在经典的图像识别任务中，用过滤器(即卷积核kernels)来导出聚合特征，而SSM也可以表示成卷积的形式

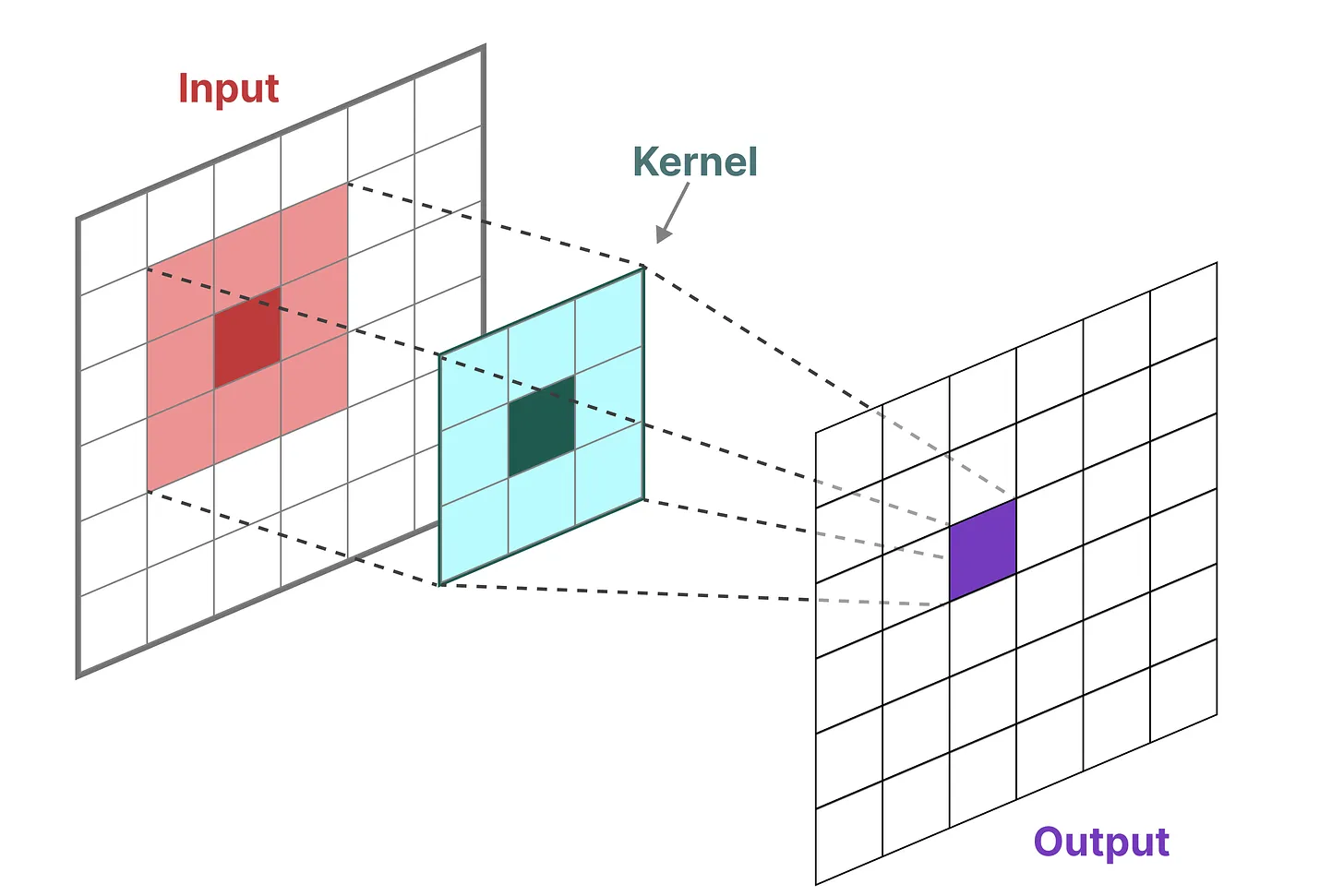
由于处理的是文本而不是图像，因此需要一维视角

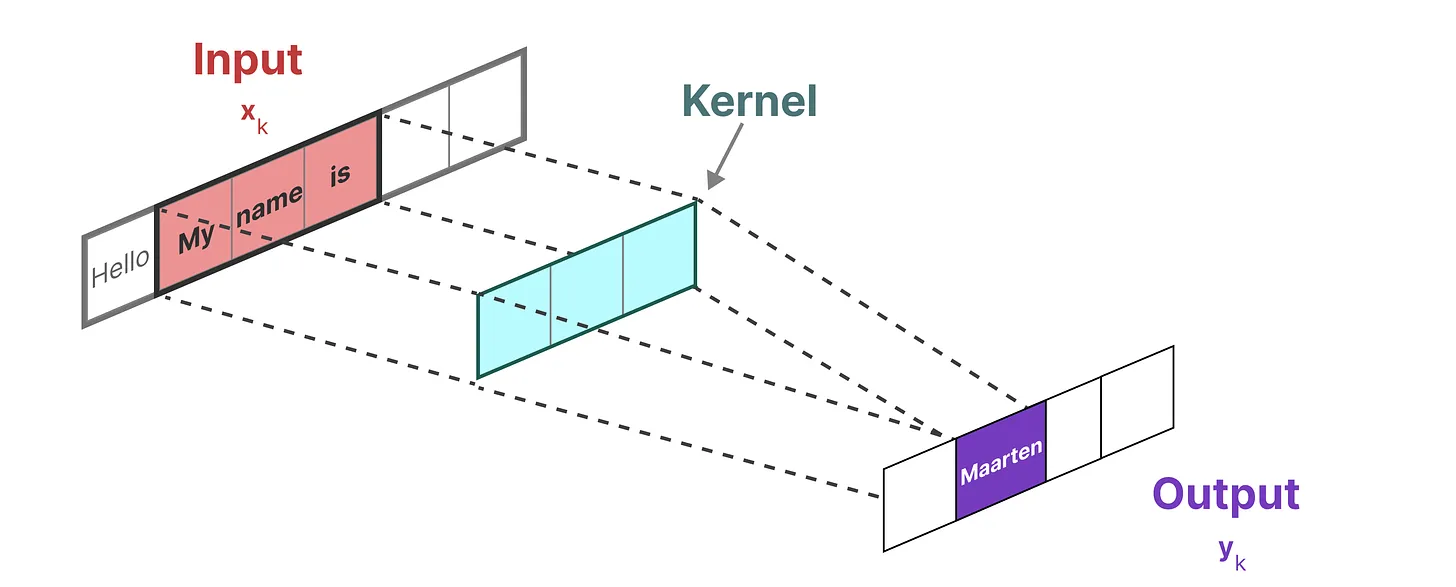
而用来表示这个“过滤器”的内核源自 SSM 公式

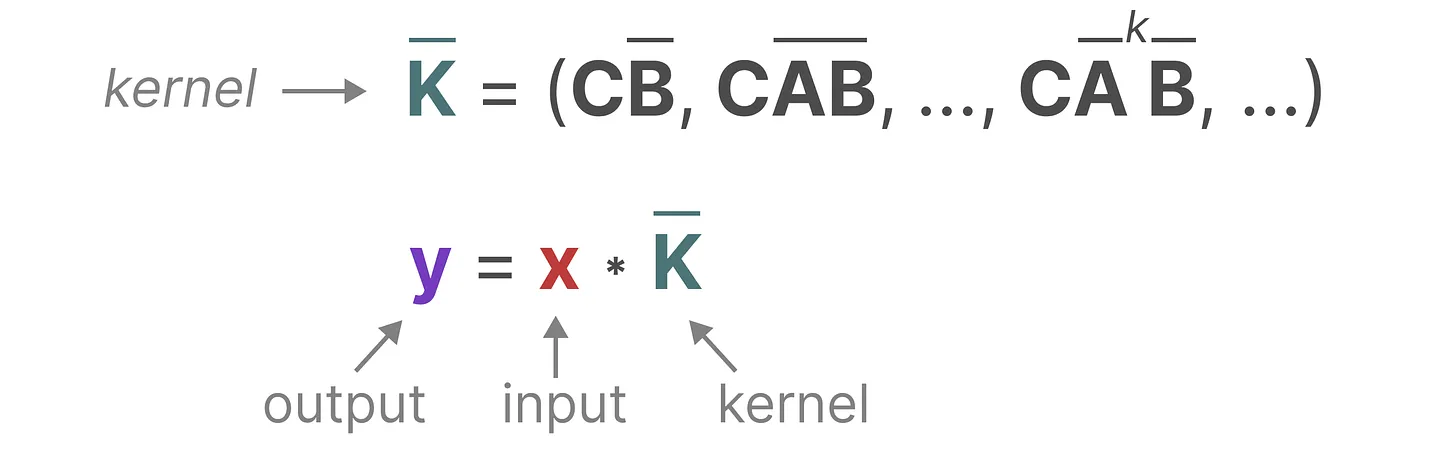
与卷积一样，可以使用 SSM 内核来检查每组token并计算输出

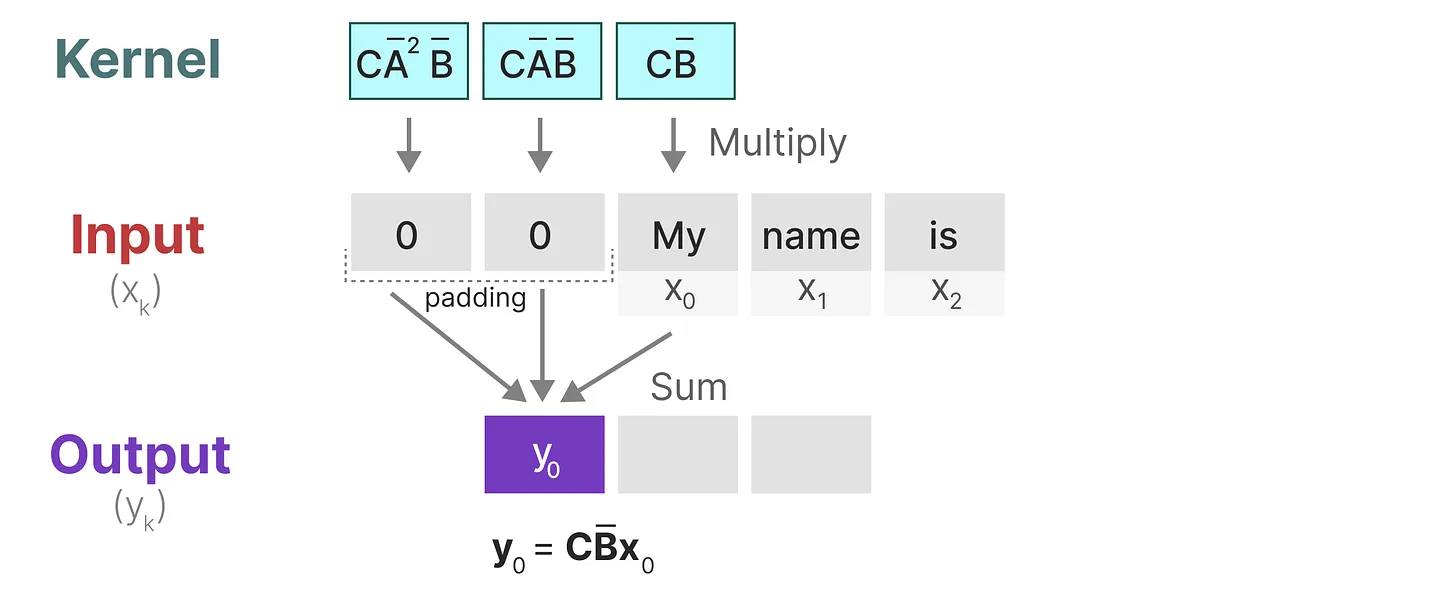
内核将移动一次以执行下一步的计算

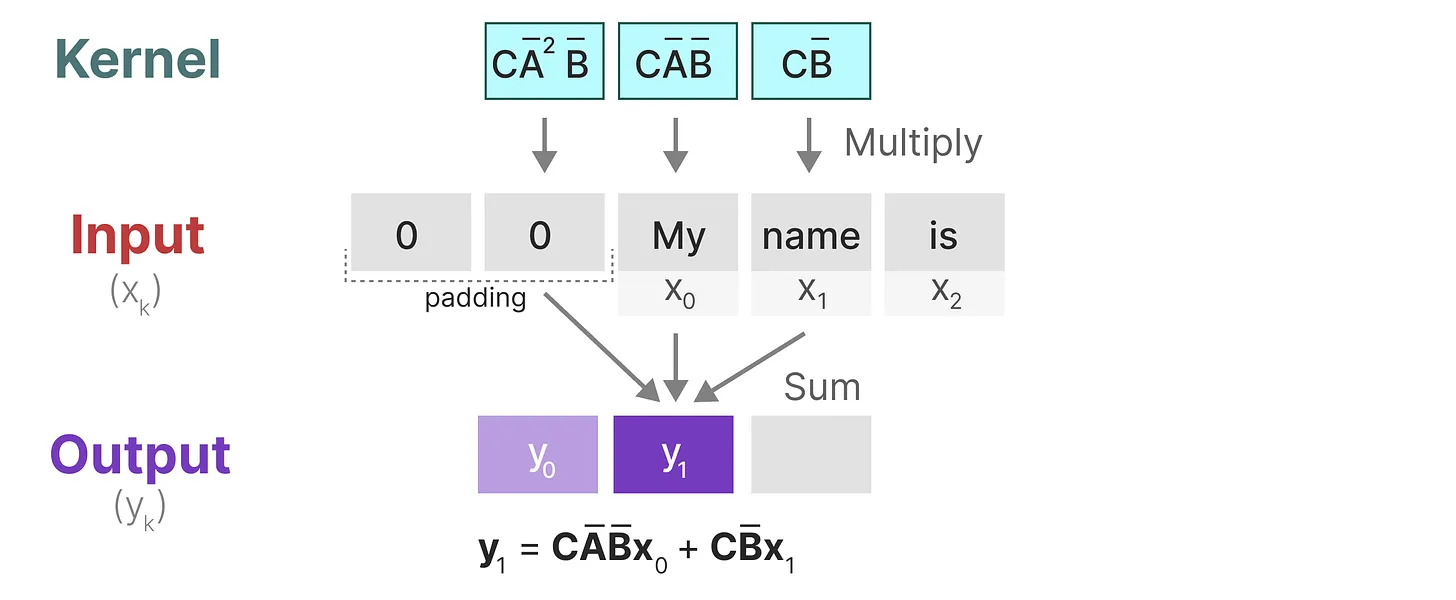
最后一步，可以看到内核的完整效果：

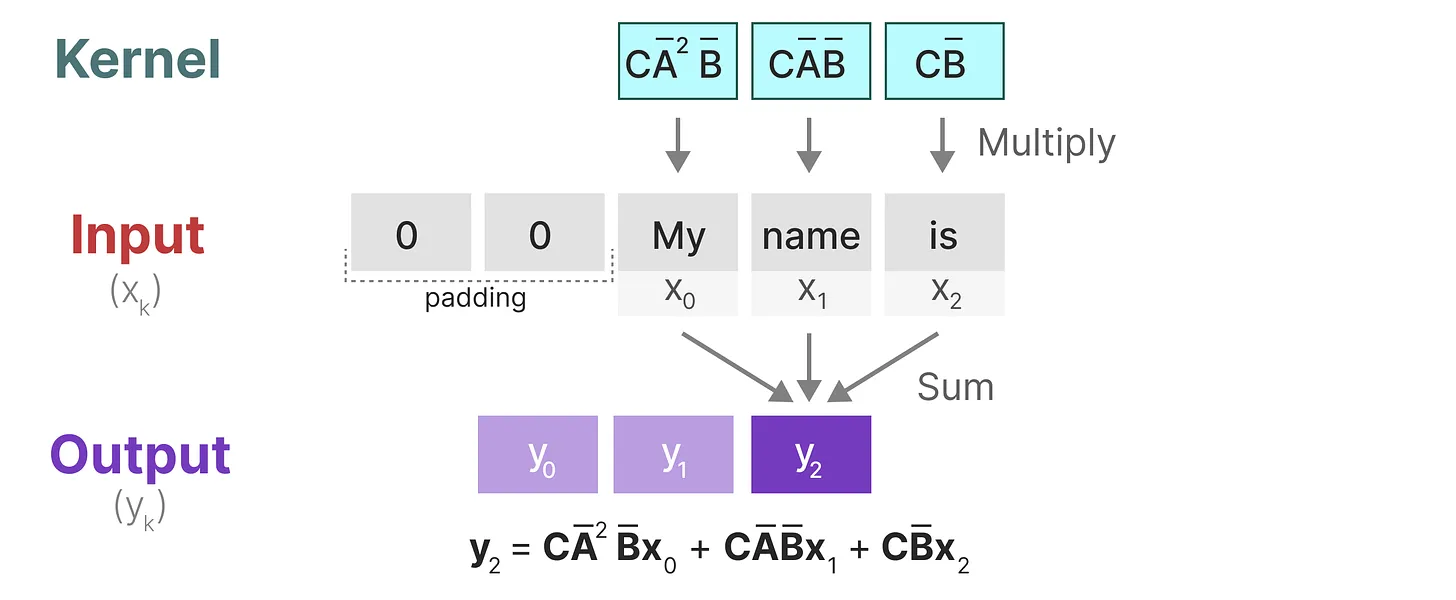
至于上图中的y_2是咋计算得到的，利用上面推导出来的以此内推，可得换个形式看，是不意味着y₃实际上可以计算为点积，其中右侧向量是输入x 由于其中三个离散参数A, B, C都是常数，因此我们可以预先计算左侧向量并将其保存为卷积核，这为我们提供了一种使用卷积超高速计算y的简单方法，如以下两个方程所示

至此，总结一下，将 SSM 表示为卷积的一个主要好处是它可以像卷积神经网络CNN一样进行并行训练。然而，由于内核大小固定，它们的推理不如 RNN 那样快速

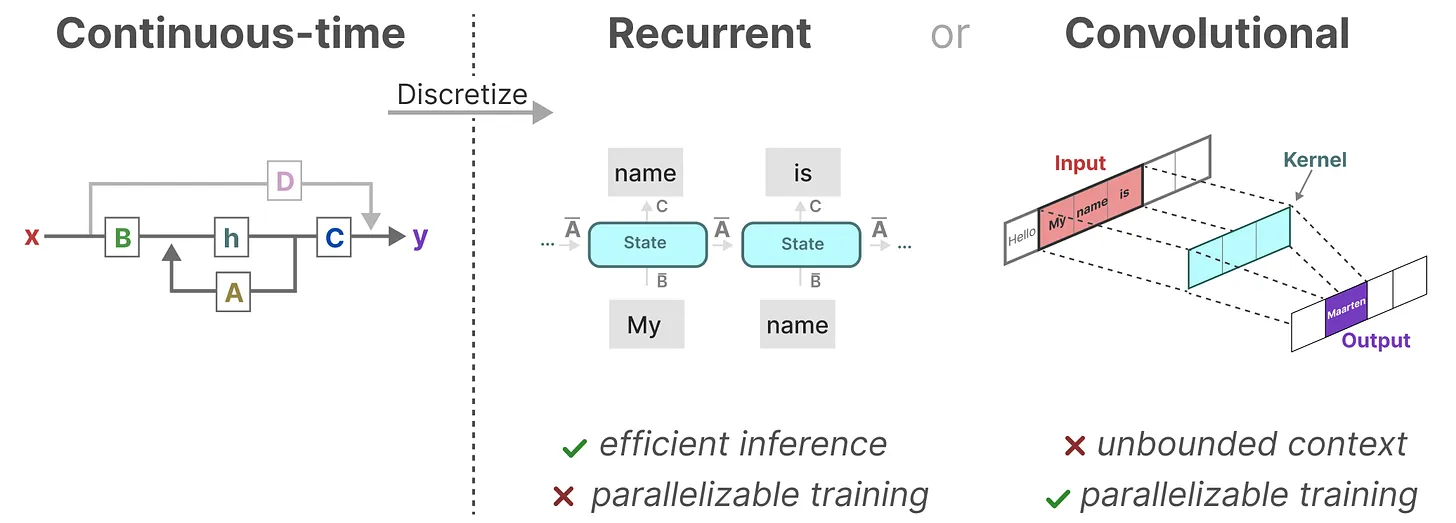
现在可以使用循环 SSM 进行有效推理，并使用卷积 SSM 进行并行训练。

作为从输入信号到输出信号的参数化映射，SSMs可以当做是RNN与CNN的结合:即推理用RNN结构，训练用CNN结构

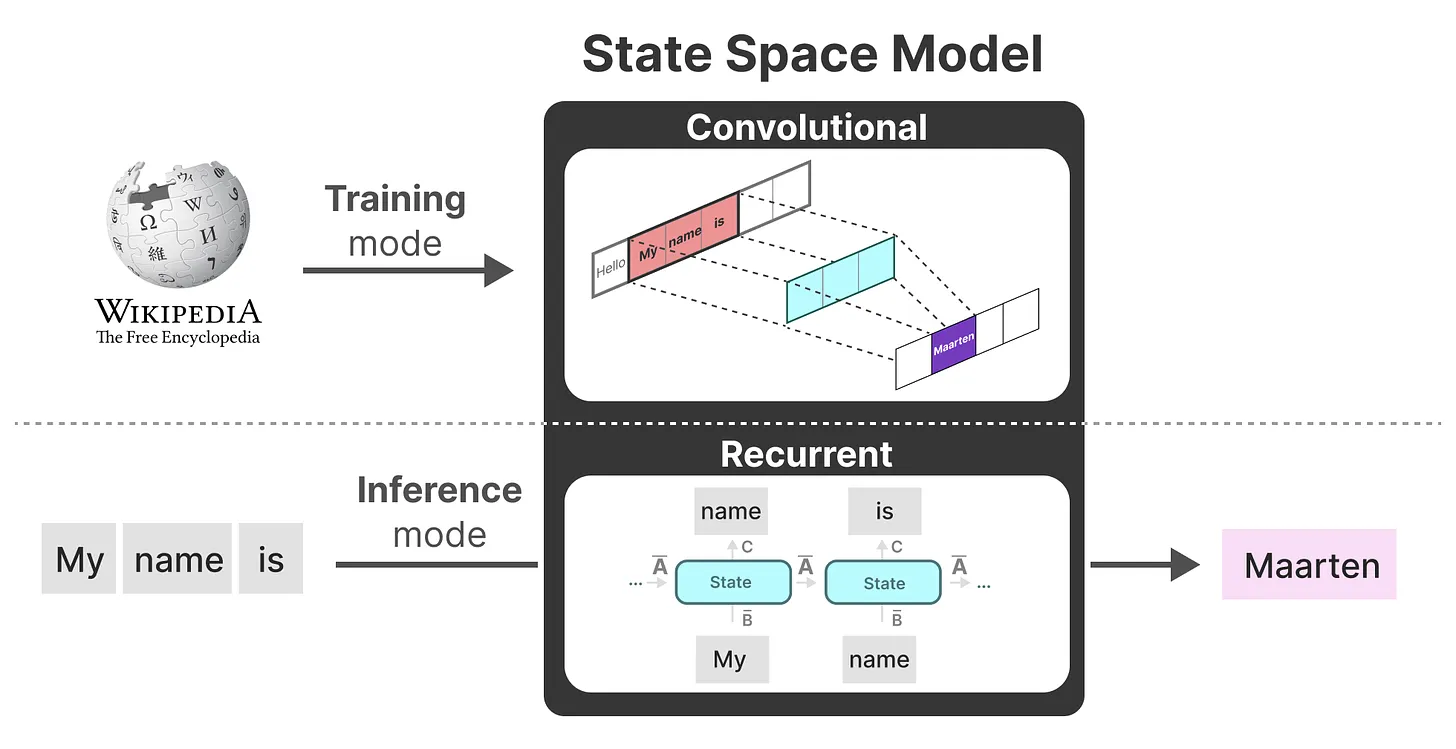
该模型称为线性状态空间层 (Linear State-Space Layer,LSSL)

总之，这类模型可以非常高效地计算为递归或卷积，在序列长度上具有线性或近线性缩放

1.3.4 长距离依赖问题的解决之道——HiPPO

如我们之前在循环表示中看到的那样，矩阵A捕获先前previous状态的信息来构建新状态(h_k = Āh_k − 1 + B̄x_k，当k = 5时，则有h₅ = Āh₄ + B̄x₅)

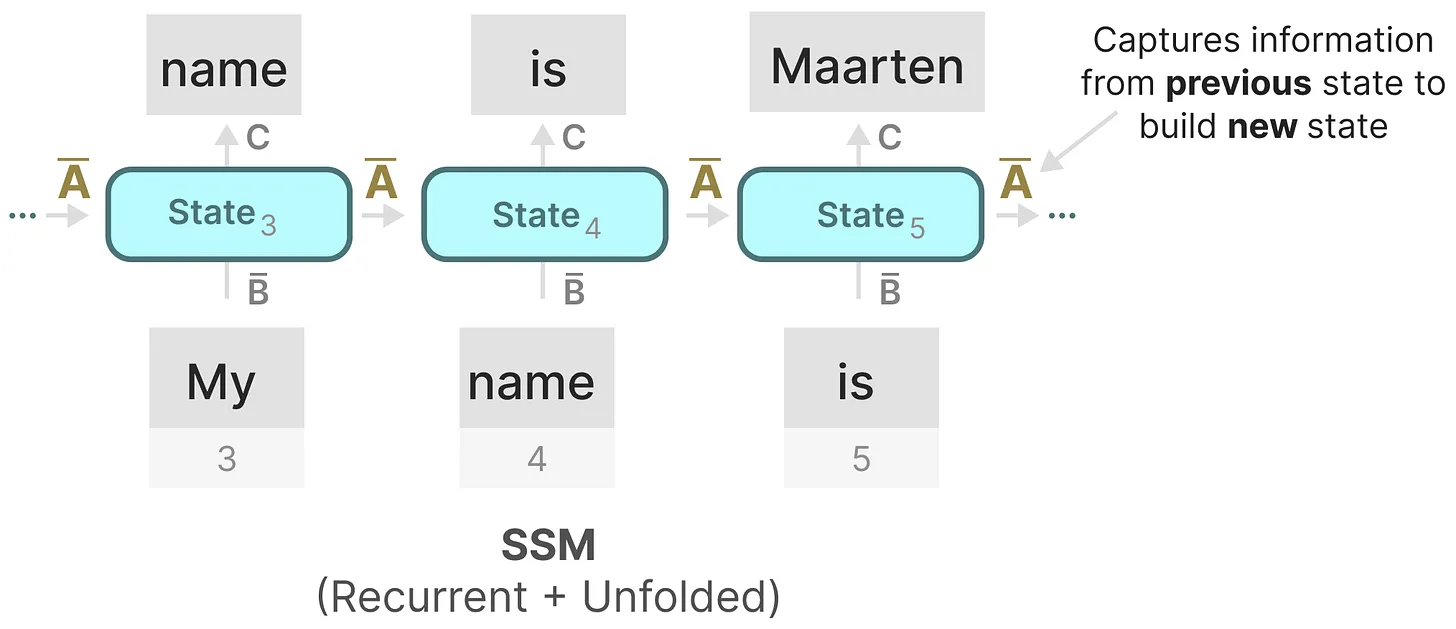
其实，某种意义上，算是矩阵A产生了隐藏状态

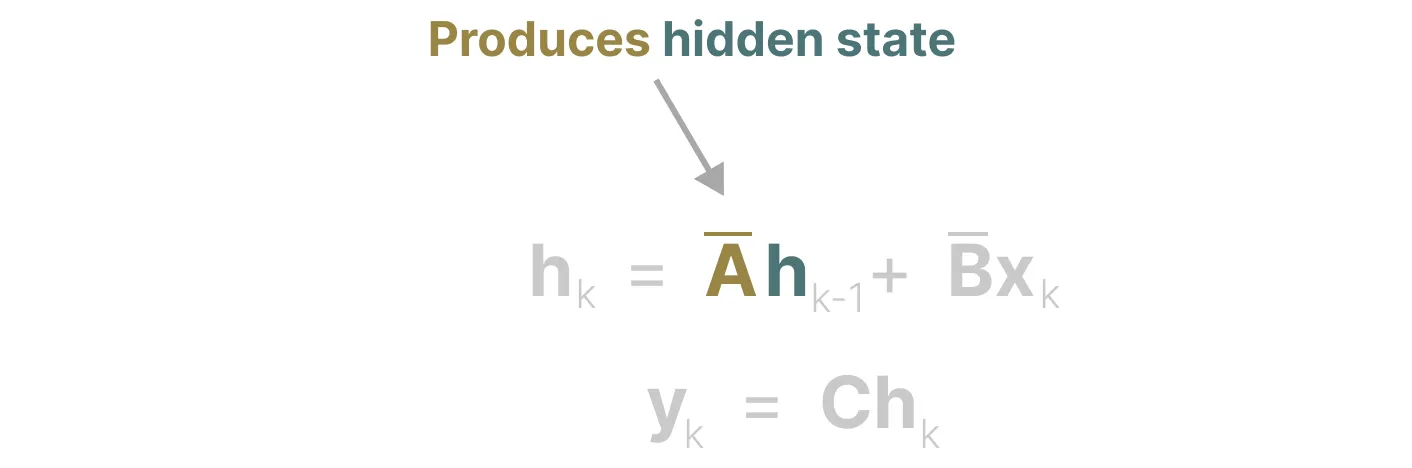
由于矩阵A只记住之前的几个token和捕获迄今为止看到的每个token之间的区别，特别是在循环表示的上下文中，因为它只回顾以前的状态。

怎样才能以保留比较长的memory的方式创建矩阵A

可以使用Hippo(Hippo的全称是High-order Polynomial Projection Operator，其对应的论文为：HiPPO: Recurrent Memory with Optimal Polynomial Projections)，解决如何在有限的存
HiPPO尝试将当前看到的所有输入信号压缩为系数向量

它使用矩阵A构建一个状态表示，可以很好地捕获最近的token并衰减旧的token。说白了，通过函数逼近产生状态矩阵A的最优解，其公式可以表示如下

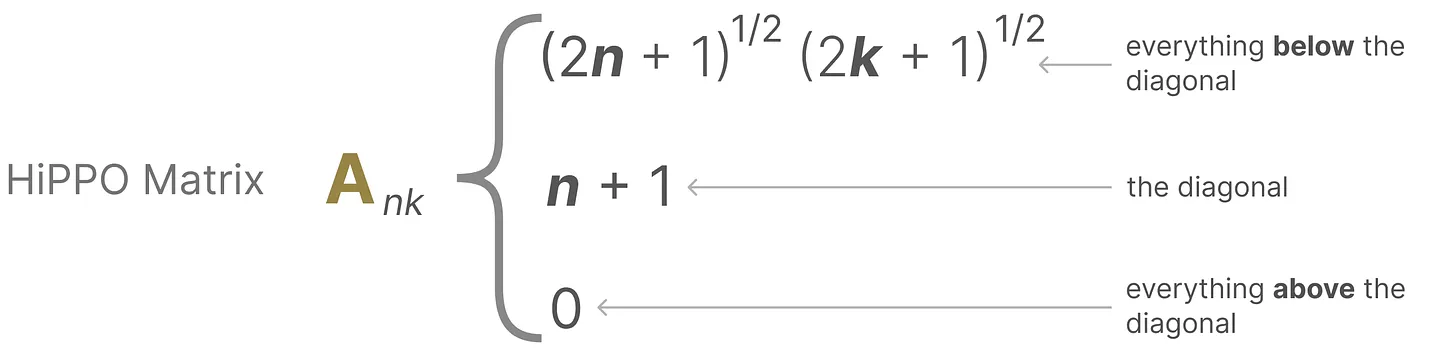
具体表示可以如下图所示

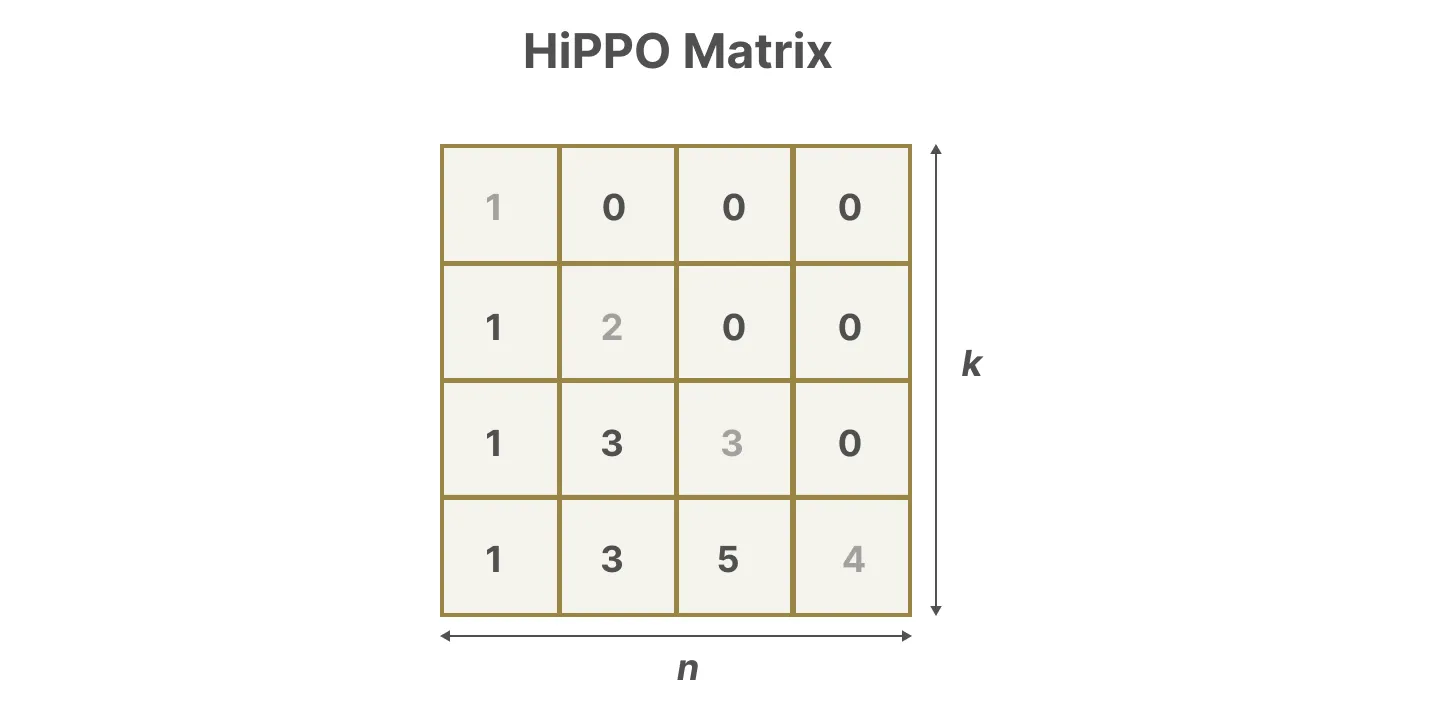
正由于HiPPO 矩阵可以产生一个隐藏状态来记住其历史(从数学上讲，它是通过跟踪Legendre polynomial的系数来实现的，这使得它能够逼近所有以前的历史)，使得在被应用于循环表示和卷积表示中时，可以处理远程依赖性

如此，S4的定义就出来了：序列的结构化状态空间——Structured State Space for Sequences，一类可以有效处理长序列的 SSM(S4所对应的论文为：Efficiently Modeling Long Sequences with Structured State Spaces)

且对矩阵A做了改进

所有 HiPPO 矩阵都具有正态加低秩 (Normal Plus Low-Rank,NPLR) 表示 A = VΛV^* − PQ^⊤ = V(Λ − (V^*P)(V^*Q)^*)V^* 对于单位V ∈ ℂ^N × N、对角线Λ 和低秩分解P, Q ∈ ℝ^N × r。这些矩阵 HiPPO- LegS、LegT、LagT 都满足r = 1 或r = 2。

1.4 SSM的问题：矩阵不随输入不同而变化，无法针对输入做针对性推理

1.4.1 SSM的问题

首先，Linear Time Invariance(LTI)规定 SSM中的A, B, C不随输入不同而不同。这意味着

于 SSM 生成的每个token，矩阵A, B, C都是相同的
使得SSM无法针对输入做针对性的推理

此外，如下图所示，无论输入x是什么，矩阵B都保持完全相同，因此与x无关

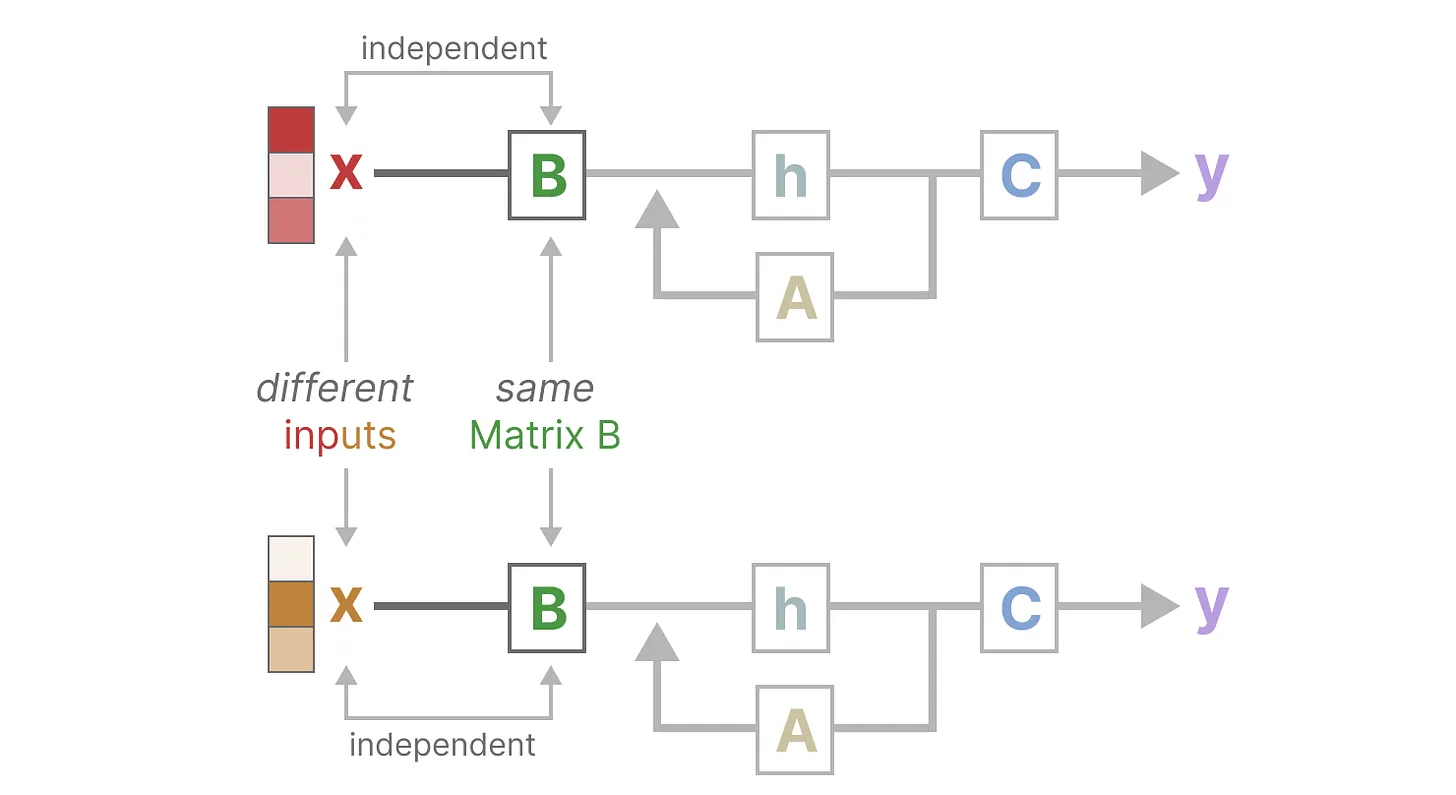
同样，无论输入如何，A和C也保持固定

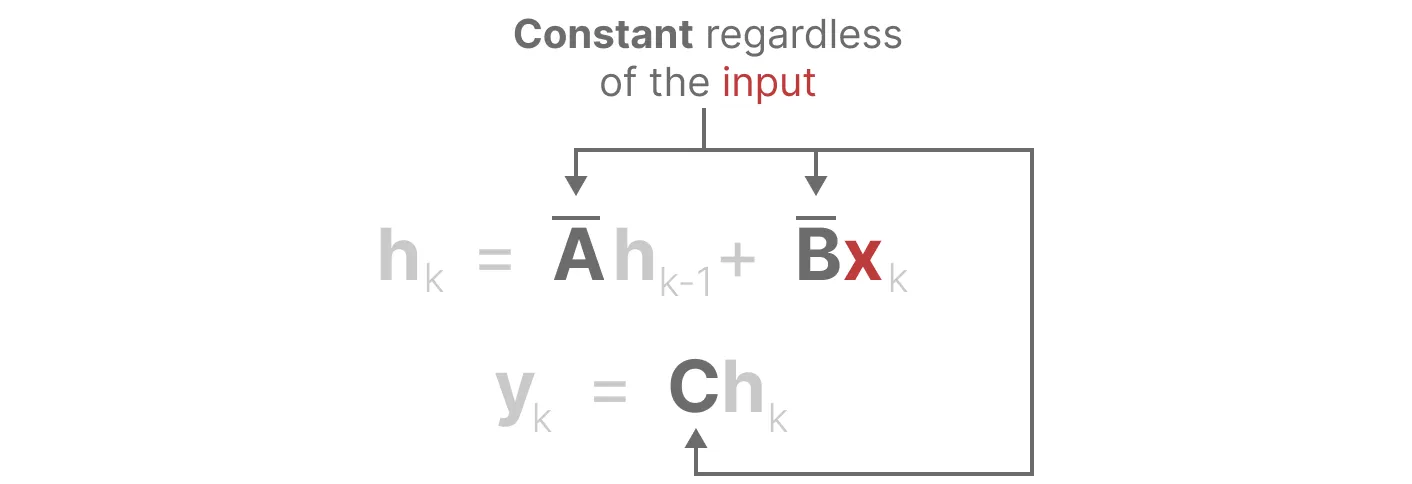
这里的不变性特指：推理时不随输入变化而变化，但在训练过程中，矩阵是可以根据需要去做梯度下降而变化的，具体来说，对于SSM和S4模型：

首先，对于训练过程：在训练时，模型会接收输入数据，并尝试预测输出。模型的参数(矩阵A, B, C的值)在每次迭代中通过梯度下降等优化算法进行调整，以便减少预测误差这意味着矩阵的值会随着训练的进行而逐渐变化，以更好地适应数据
其次，对于推理过程：一旦模型训练完成，进入推理阶段，此时矩阵A, B, C的值将固定为训练结束时学习到的值。即在推理时，模型使用这些固定的矩阵来处理新的输入数据并生成预测

即无论是SSM，还是mamba，训练时参数肯定会变这点毫无疑问

但推理时，SSM不会随着输入的不同做针对性的推理，即任何输入都是一视同仁，至于参数也不会变
但mamba会对输入做选择性推理，虽然推理时本身的参数也不会变，但会对不同的输入给予不同的有区别的对待，比如有的重点关注，有的选择性忽略

虽然Mamba模型在推理时参数本身也不变，但由于其设计中引入的选择性机制，使得模型能够根据输入数据的特点进行有区别的对待，这与SSM模型相比是一个显著的进步。且Mamba这种选择性是通过训练阶段的参数学习来实现的(根据训练阶段学习到的参数对不同的输入给予不同的处理)，而不是在推理阶段动态调整参数

1.4.2 如何改进S4

比如 “I want to order a hamburger.”这句

如果没有选择性，S4会花费相同的“精力”来处理每个单词：

但如果是一个试图对这句话的意图进行分类的模型，它可能会想更多地“关注”order、hamburger，而不是want、to 如下图所示，而通过使模型参数成为输入的函数，模型就可以做到“专注于”输入中对于当前任务更重要的部分，而这正是mamba的创新点之一

凡事也有利有弊，虽然mamba可以“专注于”输入中对于当前任务更重要的部分，但坏处是没法再通过CNN做并行训练了，原因在于：

之前计算的卷积核

在S4中，我们可以预先计算该内核、保存，并将其与输入x相乘，因为离散参数是恒定的

但在Mamba中，这些矩阵会根据输入而变化。因此，我们无法预计算，也无法使用CNN模式来训练我们的模型。从而下面这个式子用不上了

说白了，如果想要选择性，得用RNN模式进行训练，而偏偏RNN的训练速度非常慢，所以需要找到一种无需卷积的并行训练方式。

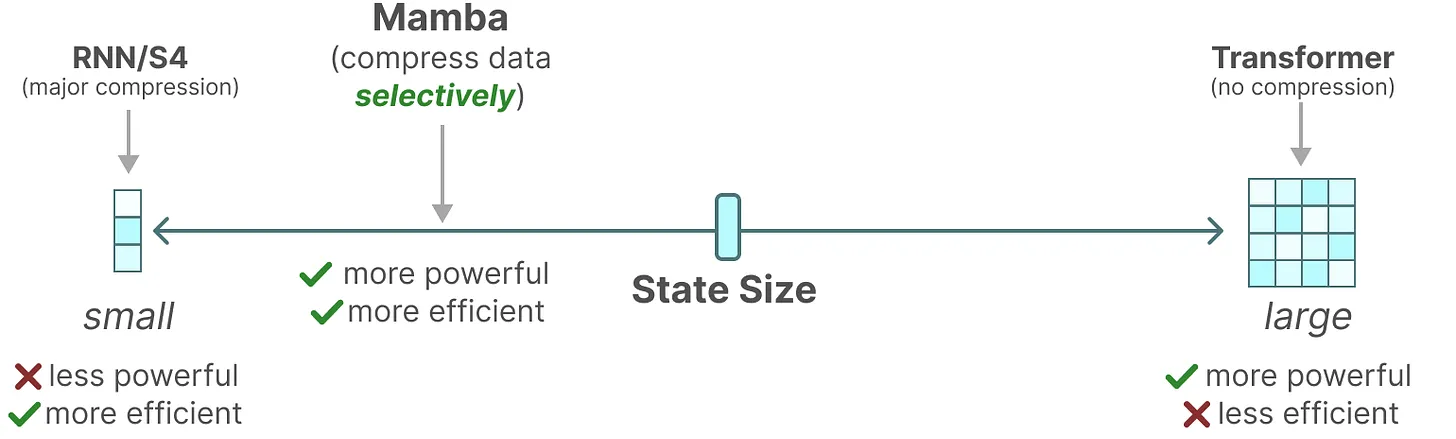
二、Mamba

Mamba(其对应论文为：Mamba: Linear-Time Sequence Modeling with Selective State Spaces，GitHub代码)，在语言、音频、DNA序列模态上都实现SOTA，在最受关注的语言任务上，Mamba-3B超越同等规模的Transformer，与两倍大的Transformer匹敌，并且相关代码、预训练模型checkpoint都已开源

简言之，Mamba是一种状态空间模型(SSM)，建立在更现代的适用于深度学习的结构化SSM (简称S6)基础上，与经典架构RNN有相似之处。

与先前的研究相比，Mamba主要有三点创新：

对输入信息有选择性处理(Selection Mechanism)
硬件感知的算法(Hardware-aware Algorithm) 该算法采用“并行扫描算法”而非“卷积”来进行模型的循环计算(使得不用CNN也能并行训练)，但为了减少GPU内存层次结构中不同级别之间的IO访问，它没有具体化扩展状态当然，这点也是受到了S5(Simplified State Space Layers for Sequence Modeling)的启发
更简单的架构将SSM架构的设计与transformer的MLP块合并为一个块，来简化过去的深度序列模型架构，从而得到一个包含selective state space的架构设计

2.1 有选择处理信息

作者认为，序列建模的一个基础问题是把上下文压缩成更小的状态，从这个角度来看

transformer的注意力机制虽然有效果但效率不算很高，毕竟其需要显式地存储整个上下文(storing the entire context，也就是KV缓存)，直接导致训练和推理消耗算力大好比，Transformer就像人类每写一个字之前，都把前面的所有字+输入都复习一遍，所以写的慢
RNN的推理和训练效率高，但性能容易受到对上下文压缩程度的限制。好比，RNN每次只参考前面固定的字数，写的快是快，但容易忘掉更前面的内容
而SSM的问题在于其中的矩阵不随输入不同而不同，即无法针对不同的输入针对性的推理
最终，Mamba的解决办法是，相比SSM压缩所有历史记录，mamba设计了一个简单的选择机制，通过“参数化SSM的输入”，让模型对信息有选择性处理，以便关注或忽略特定的输入这样一来，模型能够过滤掉与问题无关的信息，并且可以长期记住与问题相关的信息。好比，Mamba每次参考前面所有内容的一个概括，越往后写对前面内容概括得越狠，丢掉细节、保留大意

总之，序列模型的效率与效果的权衡点在于它们对状态的压缩程度：

高效的模型必须有一个小的状态(比如RNN或S4)
而有效的模型必须有一个包含来自上下文的所有必要信息的状态(比如transformer)

而Mamba为了兼顾效率和效果，选择性的关注必须关注的、过滤掉可以忽略的

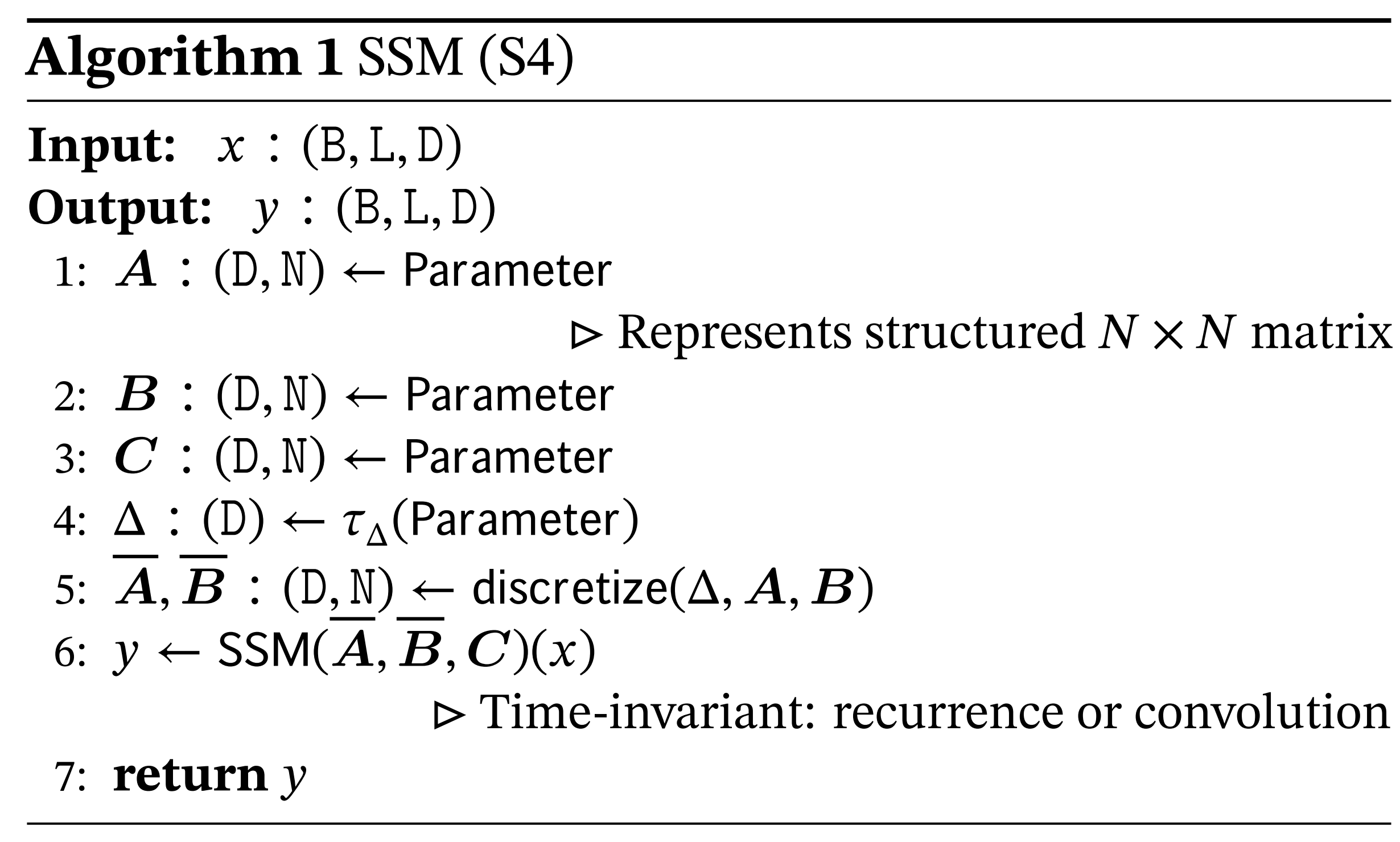
2.1.1 S4的4个参数的不随输入不同而不同

具体来说，S4 模型由四个参数 (Δ, A, B, C) 定义，它们分两个阶段定义了序列到序列的转换。

且它们不随输入变化(即与输入无关)，这些参数控制了以下两个阶段

第一阶段(1a 1b)通过固定公式和将“连续参数”(Δ, A, B)转换为“离散参数”，其中对(f_A, f_B)称为离散化规则，且可以使用多种规则来实现这一转换。

例如下述方程中定义的零阶保持(ZOH)
第二阶段(2a 2b，和3a 3b)，在参数由(Δ, A, B, C)变换为后，模型可以用两种方式计算，即线性递归(2)或全局卷积(3)

如之前所说的
- 模型通常使用卷积模式(3)可以进行高效的并行化训练其中整个输入序列提前看到，为何可以做高效的并行化呢，因为该模式能够绕过状态计算，并实现仅包含(B, L, D)的卷积核(3a)
- 并切换到循环模式(2)以高效的自回归推理(其中输入每次只看到一个时间步)

2.1.2 S4中三个矩阵的维度表示、维度变化

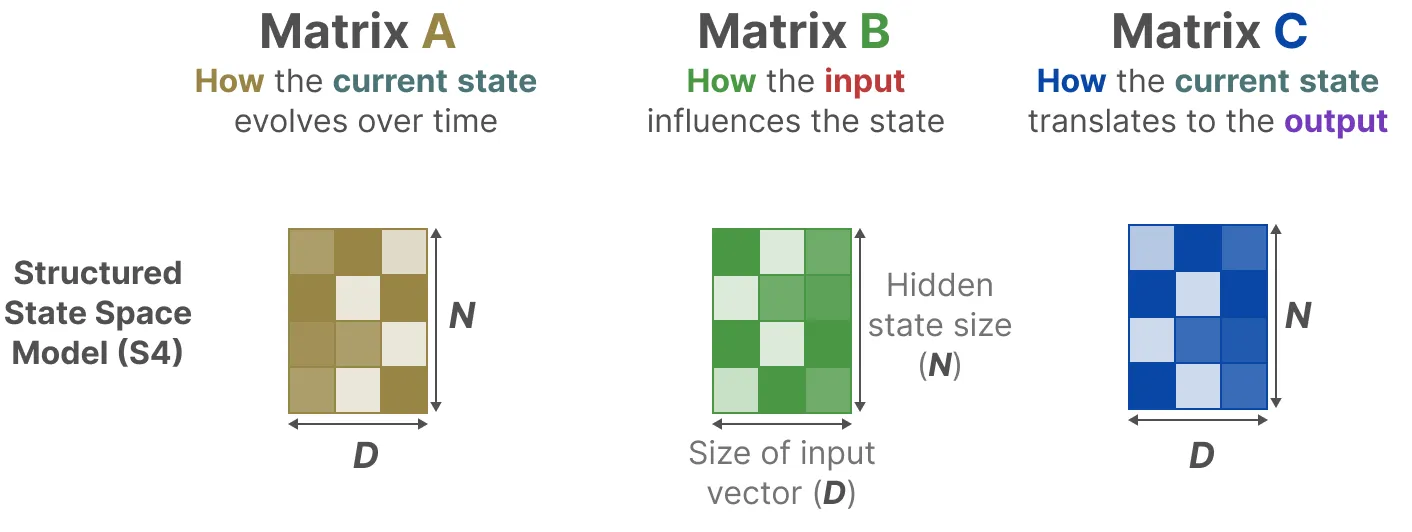
再回顾一下，通过之前的讲解，可知A ∈ ℝ^N × N, B ∈ ℝ^N × 1, C ∈ ℝ^1 × N 矩阵都可以由N个数字表示：

但为了对批量大小为B、长度为L(N ≪ L，比如类似上文举的例子中，N = 64 L = 10000)、具有D个通道的输入序列x进行操作(虽然在之前的示例中，每个token的维度设定的1，比如拿一个 64 × 64维的矩阵A 去记 10000 × 1维的数字，但实际上，经常会遇到一个token不止一个维度的，比如颜色便有R G B三个通道，即embedding的dimension是D)。x, y则是输入和输出，和 Transformer 里面一样, 他们的大小是 (batch size B x sequence length L x embedding dim D)

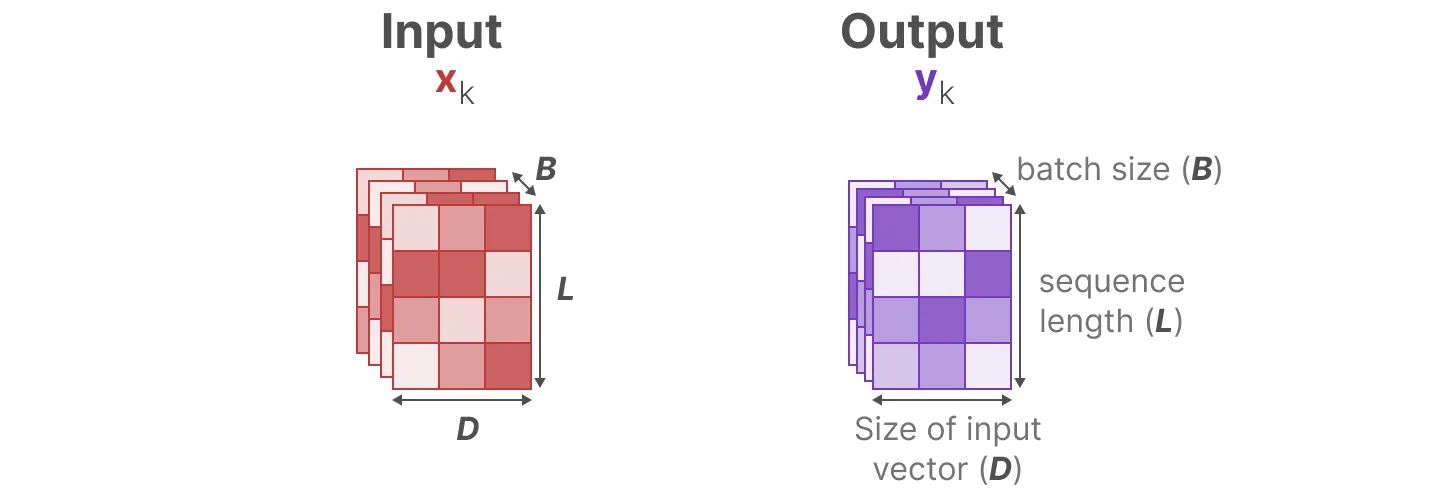
Mamba的处理方式是，给这 D 个 dimension的每个 dimension 都搞一个独立的 SSM，即SSM被独立地应用于每个通道。

这就解释了为什么下图中的A, B, C三个矩阵的第一个维度是都是 D

请注意，在这种情况下，每个输入的总隐藏状态具有DN维，在序列长度上计算它需要O(BLDN)的时间和内存。

2.1.3 Mamba：从S4到S6的算法变化流程

在Mamaba中，作者让B矩阵、C矩阵、Δ成为输入的函数，让模型能够根据输入内容自适应地调整其行为

从S4到S6的过程中
- 影响输入的B矩阵、影响状态的C矩阵的大小从原来的(D, N)变成了(B, L, N)，D指的是输入向量的维度，比如一个颜色的变量一般有R G B三个维度，N指SSM的隐藏层维度hidden dimension，当然一般设的比较小，远小于L，L指的是序列长度。
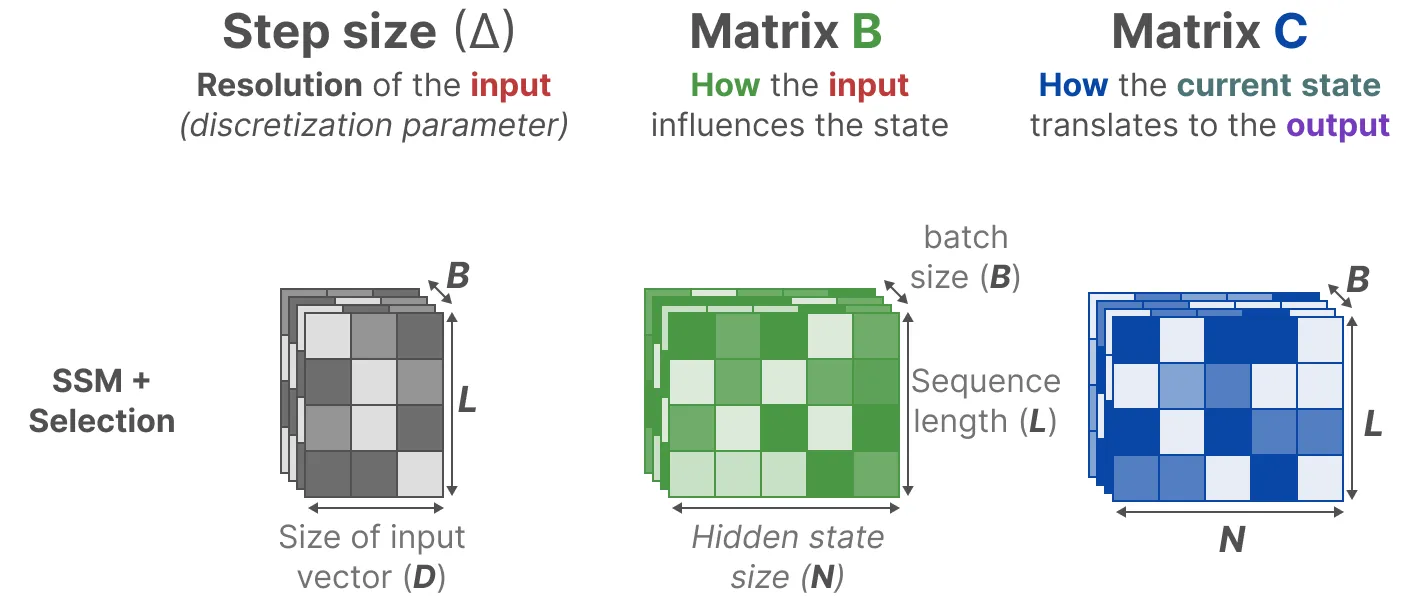
- 且Δ的大小由原来的D变成了(B, L, D)意味着对于一个batch里的每个token(总共有 B × L 个)都有一个独特的Δ且每个位置的B矩阵、C矩阵、Δ都不相同，这意味着对于每个输入token，现在都有独特不同的B矩阵、C矩阵，可以解决内容感知问题

推理时参数本身还是不变，但由于参数是数据依赖的，模型在推理时可以根据输入数据的特点进行有区别的对待，即对不同的输入token应用不同的B、C和Δ值，换言之，Mamba模型在推理时，可根据不同的输入数据动态计算矩阵B、C和步长Δ的值，但用于这些计算的参数(即决定如何计算这些矩阵和步长的函数或映射)是固定不变的。这些参数在训练阶段确定，并在推理阶段被重用(推理过程中不会对模型的参数进行重新训练或调整，而是简单地应用训练阶段学到的参数来生成预测)

维度上的变化具体执行时，是通过s_B(x) = Linear_N(x)、s_C(x) = Linear_N(x)、s_Δ(x) = Broadcast_D(Linear₁(x)) 和 τ_Δ = softplus，其中 Linear_d 是参数化投影到维度 d。选择 s_Δ 和 τ_Δ 是因为与RNN门控机制有关。
虽然A没有进行维度变化，但是通过SSM的离散化操作之后会经过outer product变成(B, L, N, D)的张量，算是以一种parameter efficient的方式来达到维度变化的目的

A离散化后，Δ的维度变化能够让整体的维度变化。

Δ，类似遗忘门这个量跟RNN里的gating有着深刻的联系，跟RNN的forgetgate的功能类似，Δ大则关注，小则忽略。

较小的步长会忽略当前输入，而更多地使用先前的上文，而较大的步长Δ会更多地关注当前输入而不是上文

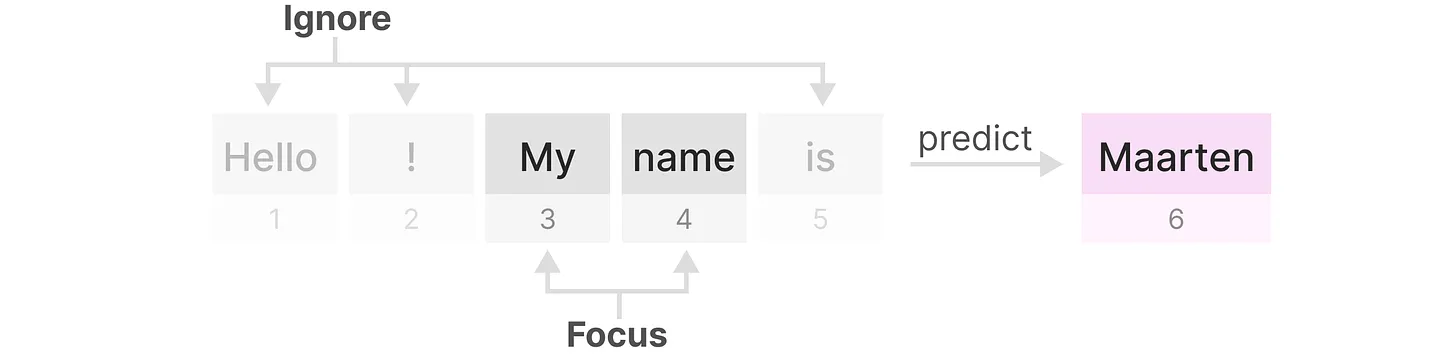
如果某个输入比较重要它的步长就更长些，被重点关注。如果某个输入不太重要它的步长就短，被直接忽略从而对于不同的输入，达到选择性关注或忽略的目标，做到详略得当主次分明。
B起到的作用类似于：进RNN的memory。C起到的作用类似于：取RNN的memory

修改B和C可以允许模型更精细地控制是否让输入x进入状态 h，或状态h进入输出 y，所以B和 C 类似于 RNN 中的输入门和输出门

A意味着对应这个维度的SSM来说，A在每个hidden state维度上的作用可以不相同，起到multi-scale/fine-grained gating的作用，这也是LSTM网络里面用element-wise product的原因

Mamba通过合并输入的序列长度和批量大小来使矩阵B和C，甚至步长Δ取决于输入(其意味着对于每个输入token，现在有不同的B和C矩阵，可以解决内容感知问题)，从而达到选择性地选择将哪些内容保留在隐藏状态以及忽略哪些内容的目标

2.2 硬件感知的设计：并行扫描(parallel scan)

由于A, B, C这些矩阵现在是动态的了，因此无法使用卷积表示来计算它们(CNN需要固定的内核)，因此，只能使用循环表示，如此也就而失去了卷积提供的并行训练能力。

为了实现并行化：

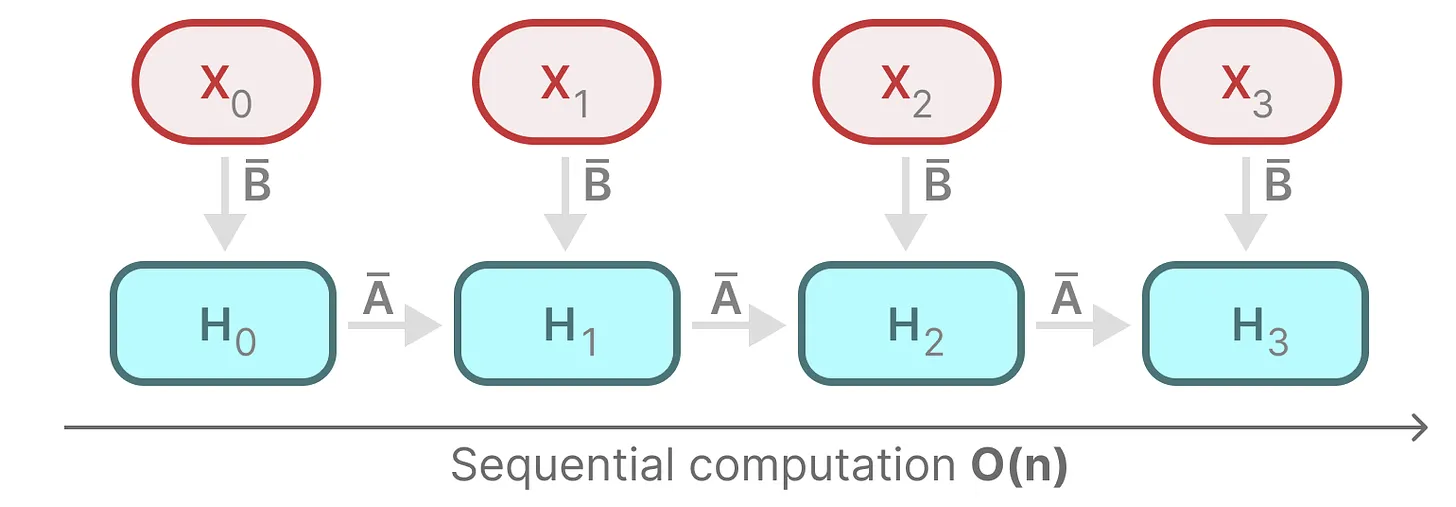
每个状态比如H₁都是前一个状态比如H₀乘以，加上当前输入X₁乘以的总和，这就叫扫描操作(scan operation)，可以使用 for 循环轻松计算，然这种状态之下想并行化是不可能的

Mamba通过并行扫描(parallel scan)算法使得最终并行化成为可能，其假设执行操作的顺序与关联属性无关因此，可以分段计算序列并迭代地组合它们，即动态矩阵B和C以及并行扫描算法一起创建选择性扫描算法(selective scan algorithm)

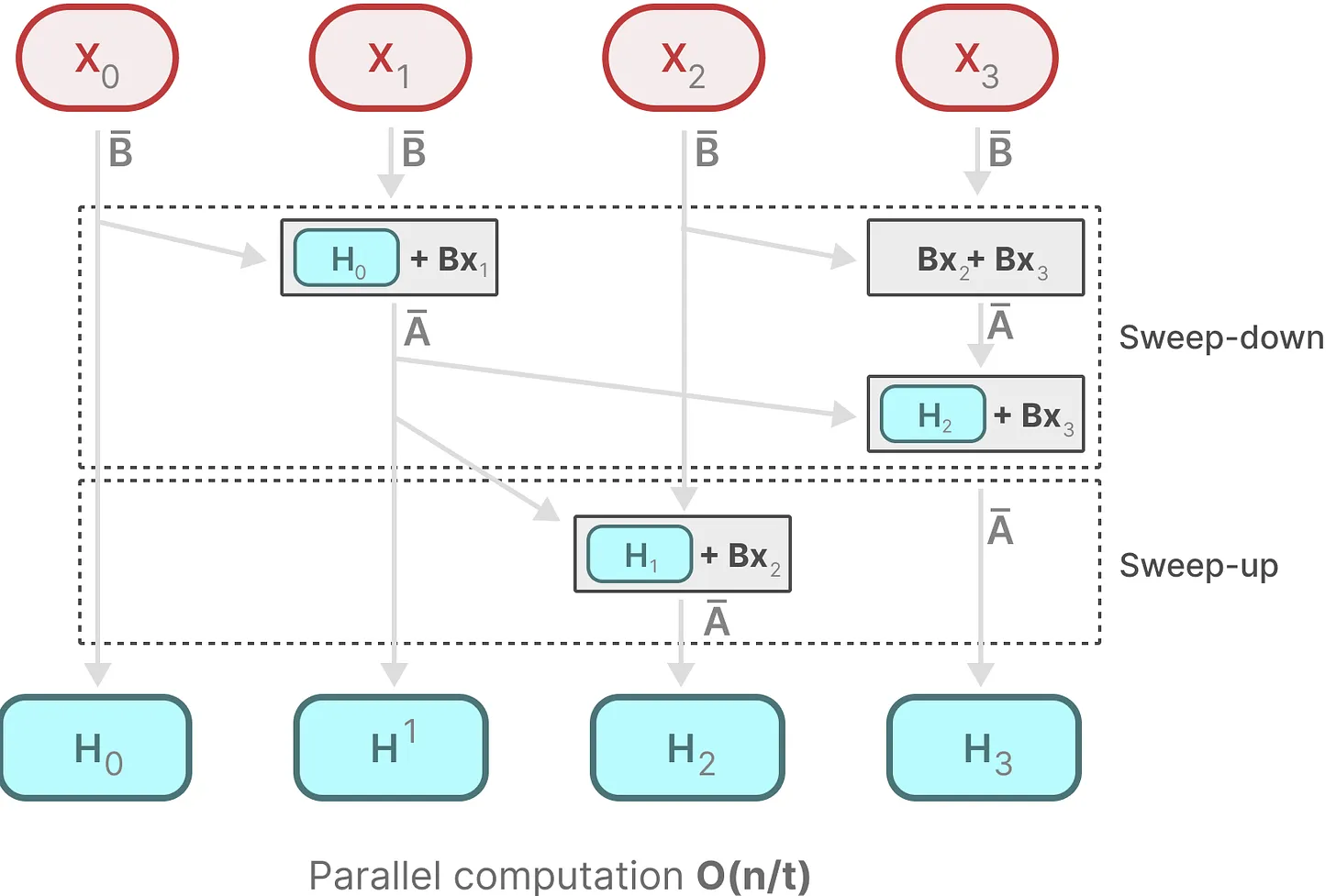
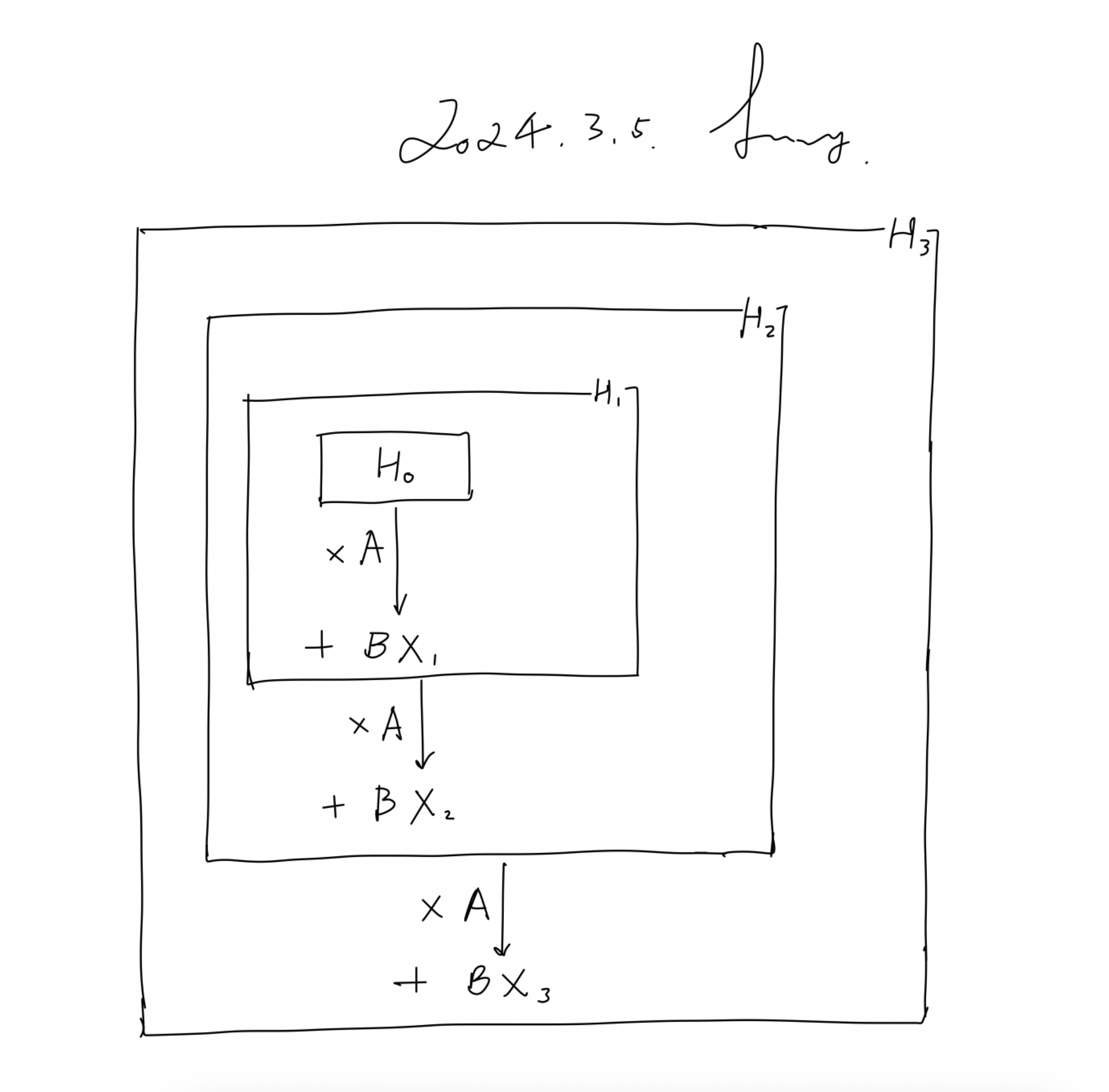
时间复杂度 O(n/t) 中的 t ，通常代表用于执行任务的处理器或计算单元的数量。所以才有，如果一个任务在单核上运行需要 O(n) 时间，则在 t 核上并行运行时，理想情况下可以将时间复杂度降低到O(n/t)

把相关推导再拆解一下，以更一目了然

首先，H₁和H₂的计算很简单，如下所示

* 其次，H₃可以由H₂计算得来，可以由H₁甚至H₀计算得来

最后，H₃最终包含了之前H₂、H₁以及X₁, X₂, X₃的信息，只是做了整体的压缩

此外，为了让传统的SSM在现代GPU上也能高效计算，Mamba中也使用了Flash Attention技术

简而言之，利用内存的不同层级结构处理SSM的状态，减少高带宽但慢速的HBM内存反复读写这个瓶颈
具体而言，就是限制需要从 DRAM 到 SRAM 的次数(通过内核融合kernel fusion来实现)，避免一有个结果便从SRAM写入到DRAM，而是待SRAM中有一批结果再集中写入DRAM中，从而降低来回读写的次数

2.3 简化的SSM架构及最终的整体流程

将大多数SSM架构比如H3的基础块，与现代神经网络比如transformer中普遍存在的门控MLP相结合，组成新的Mamba块，重复这个块，与归一化和残差连接结合，便构成了Mamba架构。

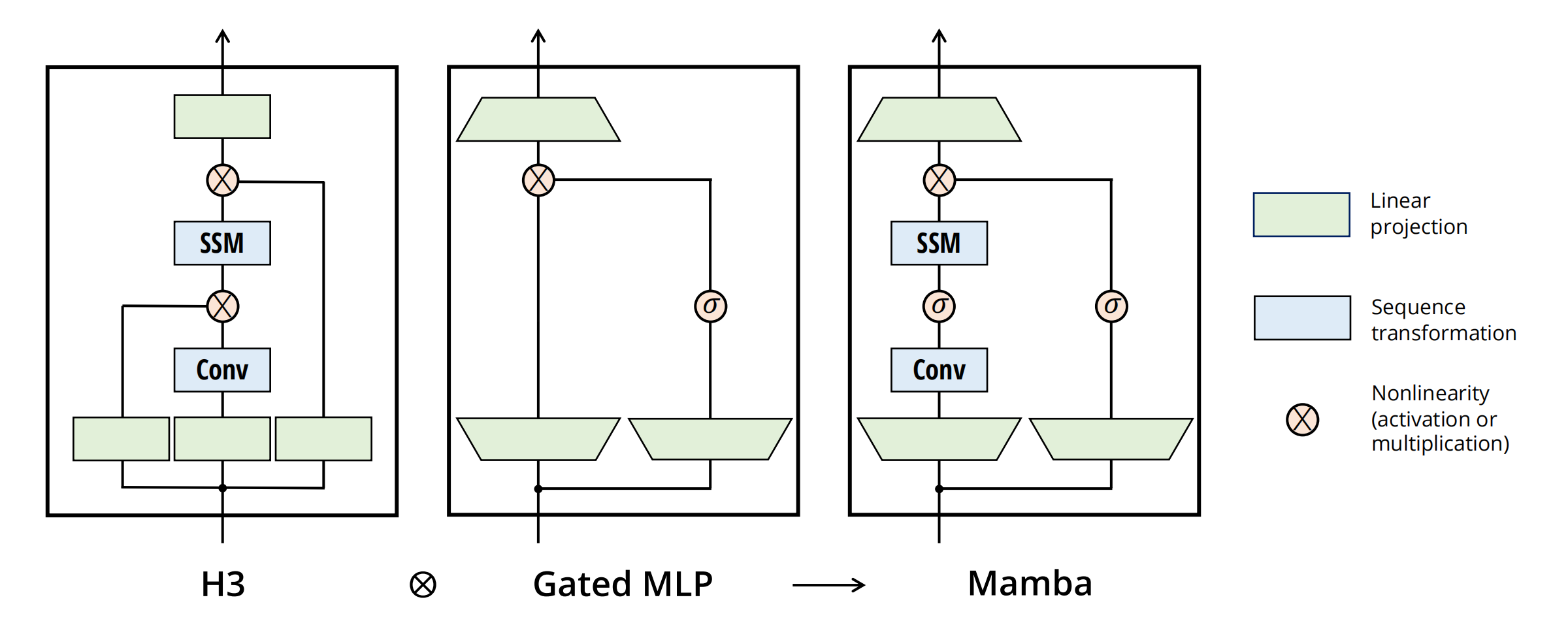
关于mamba的整体架构，有两点值得强调下

为何要做线性投影

经过线性投影后，输入嵌入的维度可能会增加，以便让模型能够处理更高维度的特征空间，从而捕获更细致、更复杂的特征。
为什么SSM前面有个卷积本质是对数据做进一步的预处理，更细节的原因在于：
- SSM之前的CNN负责提取局部特征(因其擅长捕捉局部的短距离特征)，而SSM则负责处理这些特征并捕捉序列数据中的长期依赖关系，两者算互为补充
- CNN有助于建立token之间的局部上下文关系，从而防止独立的token计算。毕竟如果每个 token 独立计算，那么模型就会丢失序列中 token 之间的上下文信息。通过先进行卷积操作，可以确保在进入 SSM 之前，序列中的每个 token 已经考虑了其邻居 token 的信息。这样，模型就不会单独地处理每个 token，而是在处理时考虑了整个局部上下文

最终在更高速的SRAM内存中执行离散化和递归操作，再将输出写回HBM，具体来说

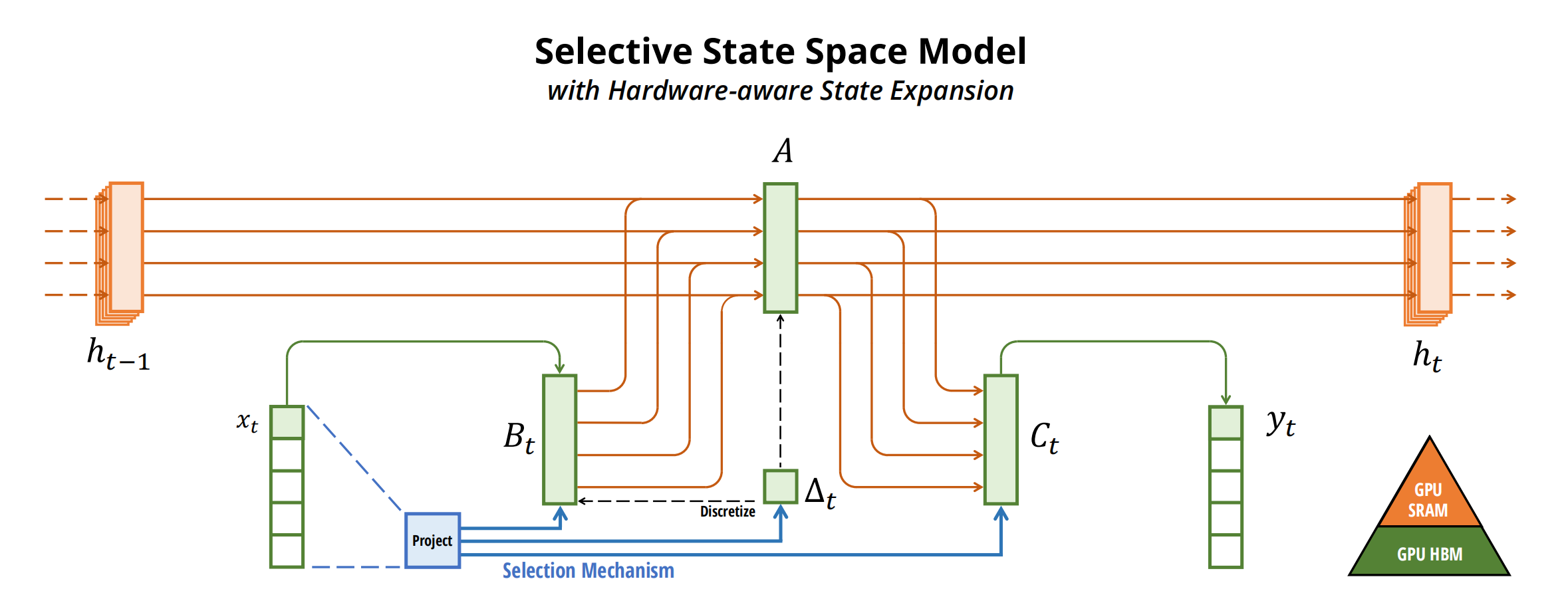
不是在GPU HBM(高带宽内存)中将大小为(B, L, D, N)的扫描输入进(A, B)，而是直接将SSM参数(Δ, A, B, C)从慢速HBM加载到快速SRAM中
然后，在SRAM中进行离散化，得到(B, L, D, N)的
接着，在SRAM中进行scan得到(B, L, D, N)的输出
最后，multiply and sum with C，得到(B, L, D)的最终输出写回HBM

2.4 Mamba的应用实例

2.4.1 通过mamba预测下一个token的示例

首先进行线性投影以扩展输入嵌入，然后，在应用选择性 SSM之前先进行卷积(如上节所说，以防止独立的token计算)

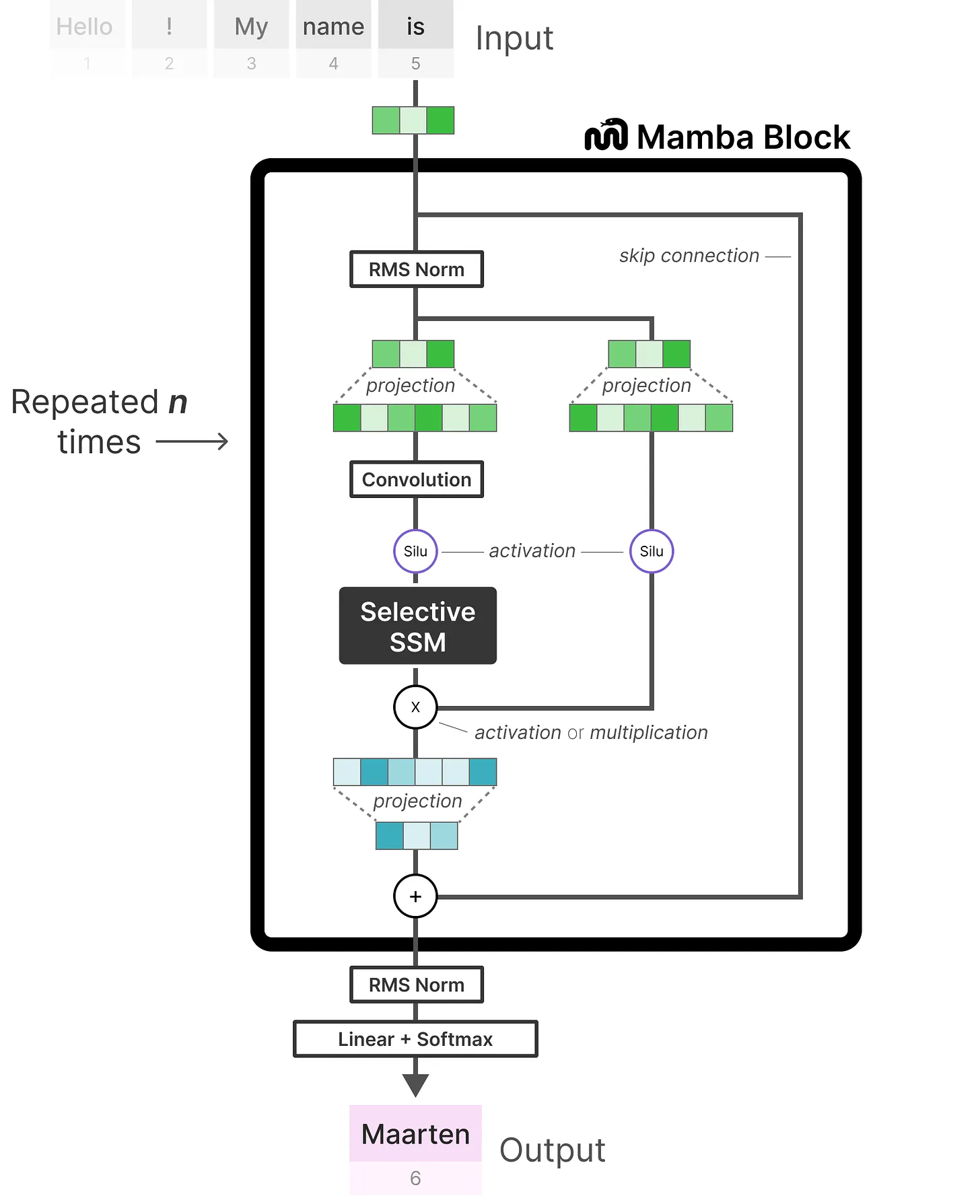
其中的“选择性SSM(即Selective SSM)”具有以下属性

Recurrent SSM通过离散化创建循环SSM
HiPPO对矩阵A进行初始化A以捕获长程依赖性
选择性扫描算法(Selective scan algorithm)选择性压缩信息
硬件感知算法(Hardware-aware algorithm)加速计算

最后，包含归一化层和用于选择“预测的token”的softmax

2.4.2 三个任务的对比：coping、selective copying、induction heads

如下图所示，有三个任务

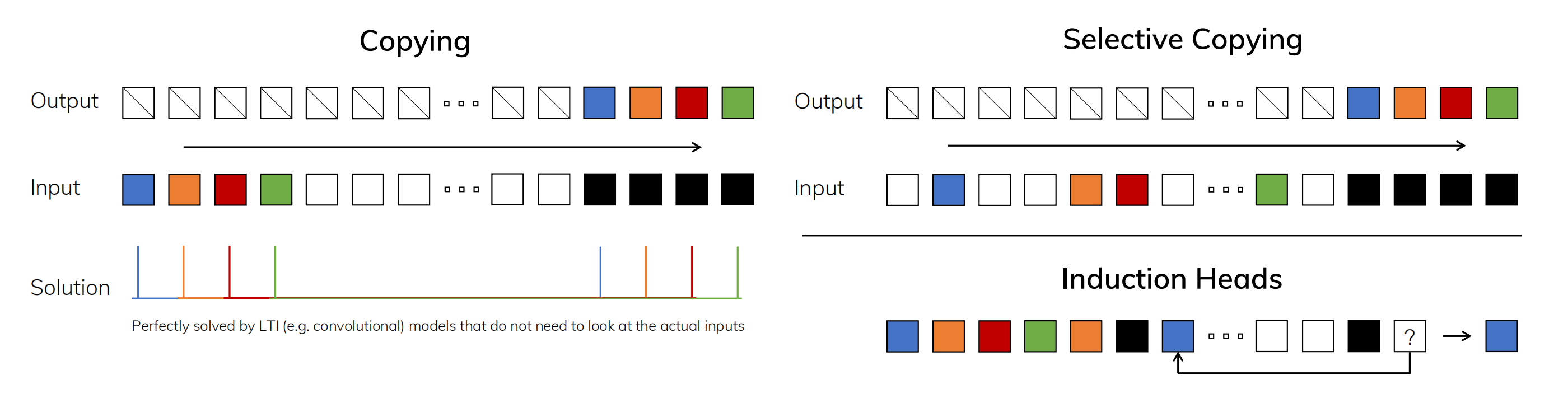
(左)复制任务的标准版本涉及输入和输出元素之间的固定间距，可以通过线性递归和全局卷积等时不变模型轻松解决
(右上)选择性复制任务在输入之间具有随机间距，需要使用时变模型，在内容上能够灵活地选择记忆或忽略输入相当于选择性复制任务通过改变“要记忆的tokens的位置”来改进纯粹的复制任务。它需要内容感知推理，以便能够记住相关的标记(有色)，并过滤掉不相关的标记(白色)。
(右下)归纳头部任务是联想回忆的一个例子，需要根据上下文检索答案，这是LLM关键的能力其实，归纳头部任务是一种众所周知的机制，据推测可以解释LLMs的大部分上下文学习能力。它需要上下文感知的推理，以便知道何时在适当的上下文中产生正确的输出(黑色)。

三、 Mamba-2

Mamba-2(论文:Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality，GitHub代码)。

Mamba-2通过将结构化SSM（S4）与注意力变体连接起来，称之为结构化状态空间对偶 (State Space Duality，SSD)，该框架是通过结构化矩阵的抽象而形成的。作者提出了两个广泛的框架来表示序列模型，一个是矩阵变换，另一个是张量收缩，每种都揭示了对偶性的不同视角。技术贡献包括：

展示了SSM和半可分矩阵之间的等价性。计算状态空间模型的不同方法可以重新定义为结构化矩阵上的各种矩阵乘法算法。
改进了线性注意力理论，并推广到新的结构化掩蔽注意力（SMA）。
连接SSM和SMA，证明了它们之间有很大的交集，并且是彼此的对偶。

3.1 概述

Mamba-2 论文的要点是结构化状态空间对偶性（SSD），它指的是几个方面：

SSD 模型是指特定的独立层，例如注意力或 SSM，可以合并到深度神经网络中
SSD框架是推理该模型（以及更多理论联系）的通用框架
SSD算法是一种比以前的SSM更高效地计算SSD层的算法

3.1.1 线性 (SSM) 模式

SSD 从与 Mamba 相同的一组方程开始：

(Selective state space model(SSM))

结构化状态空间模型 (SSM)定义了x ∈ ℝ^T ↦ y ∈ ℝ^T 映射。将x_t和y_t视为标量，将隐藏状态h_t视为N维向量，其中N是一个独立的超参数，称为状态大小、状态维度或状态扩展因子。

选择性状态空间模型允许(A, B, C) SSM 参数随时间变化。它们形状分别为 A ∈ ℝ^{(T, N, N)}, B ∈ ℝ^(T, N), C ∈ ℝ^(T, N)的张量。与 Mamba-1 一样，将一切都置于实数ℝ之上，尽管与其他结构化 SSM（如 S4 谱系）一样存在复杂的变体。

结构化SSM需要A具有可有效计算的结构，例如最常用的对角线结构^[1] ^[2] ^[3] ^[4]。在这种情况下，A ∈ ℝ^(T, N)，其中仅存储N × N矩阵的对角线元素。

3.1.2 SSD：标量结构化 SSM

最初的 Mamba（或者更准确地说是其核心“S6”层）正是具有对角结构的选择性 SSM。Mamba-2 的 SSD 层仅做了一个小修改:它将对角线A进一步限制为标量倍恒等结构；换句话说，A的对角线元素必须都是相同的值。在这种情况下，A可以用形状(T)表示，也可以将A_t识别为只是一个标量（所以有时将其表示为a_t）。

多头SSMS

方程仅针对单维输入 x ∈ ℝ^T定义。如果X ∈ ℝ^(T, P)有P个单独的通道，可以为每个通道独立使用相同的动态（即相同的 SSM(A, B, C)）。这可以解释为SSM模型的单头。在这里，将X视为形状(T, P)的张量，其中T是序列（时间）维度，P是“头部尺寸”通常，在实现这些模型时会有一个额外的批量维度B，在整个演示中忽略它。

多个头可完全独立构造；假设正在使用一个头。请注意，这些头与多头注意力模型中的头的工作方式完全相同，并且在 Mamba-2 中，选择与现代 Transformer 类似的尺寸，例如P = 64或P = 128。（为了缩放到更大的模型宽度D = d_model，保持这个固定并增加独立头的数量。）可以将一般（选择性）状态空间模型表示为

Y^(T, P) = SSM(A^(T, ⋯), B^(T, N), C^(T, N))(X^(T, P))

一些变化轴包括

A上的结构影响其参数形状：
- ⋯ = (N, N)适用于一般（非结构化）SSM
- ⋯ = (N)用于对角 SSM（或其他结构，例如对角加低秩^[1]）
- ⋯ = () 用于标量 SSM（即 SSD）
状态维度N(d_state)
头部尺寸P(d_head)

结构化 SSM 还有其他变化轴（例如，时不变性与选择性、SISO 与 MIMO ^[4]、真实与复杂等）。

3.1.3 二次（注意力）模式

首先，暂时忘掉状态空间模型。给定上面相同的张量和相同的形状A ∈ ℝ^(T), B ∈ ℝ^(T, N), C ∈ ℝ^(T, N)，定义一个不同的对象。首先，定义以下矩阵

然后，定义以下矩阵

M = L ∘ CB^⊤ ∈ ℝ^(T, T)

最后，M编码序列变换x ∈ ℝ^T ↦ y ∈ ℝ^T，将一维输入映射到一维输出就像方程通过基本矩阵乘法y = Mx。这看起来与注意力计算非常相似。事实上，如果都是a_t = 1，那么L只是下三角因果掩模(causal mask)，而相当于因果线性注意力(causal linear attention)。

Y = (L ∘ QK^⊤)V

如果重命名(C, B, X) ↦ (Q, K, V)这与方程完全相同！

3.1.4 状态空间对偶性(State Space Duality,SSD)

所谓“对偶性”是指方程（对于标量恒等结构 A_t情况）和中定义的两个模型是实际上是完全相同的模型，可以将其视为特定的函数

(A^(T), B^(T, N), C^(T, N), X^(T, P)) ↦ Y^(T, P)

在通用 SSD 框架中，将以两种完全不同的方式展示这种等价性，这两种方式实际上都更加通用，并且都非常具有启发性。

SSD vs. SSM

与以前的 SSM 相比，SSD 与 Mamba 的核心层几乎相同，但在循环A矩阵上具有更多结构。

Mamba-1 (S6) 在A上使用对角线结构，而 Mamba-2 (SSD) 在A上使用标量乘以恒等结构。
Mamba-1 的头部尺寸为P = 1（即所有通道完全由单独的 SSM 独立控制），而 Mamba-2 使用的头部尺寸为P > 1（类似于P = 64）。

特别是，这可以通过两种方式被视为与权重相关：

通过将 A的对角结构限制为标量乘以恒等式，递归动态在状态空间的所有N元素之间共享。
这些动态也会在给定头部的所有P通道之间共享。

换句话说，单个 SSM 头具有总状态大小P × N，每个状态大小都由 Mamba-1 中单独的标量循环控制，但在 Mamba-2 中由单个共享循环控制。这些变化对于能够以二次注意力模式查看模型是必要的，这允许使用矩阵乘法。与 Mamba-1 相比，Mamba-2 允许更大的状态维度（从 Mamba-1 中的N = 16到N = 64到N = 256甚至 Mamba-2 中更高），同时在训练过程中速度更快。

SSD vs. Attention

与标准（自）注意力相比，SSD 也只有两点不同：

softmax 归一化被删除。
乘法应用单独的元素掩码矩阵。

第一个差异可以解释为将模型的有效状态大小从线性减小到恒定，并将其效率从二次提高到线性。第二个区别是 SSD 与标准线性注意力的区别。将掩码视为依赖于输入的相对位置编码的一种方法。由于中的掩码L，标准注意力分数⟨Q_i, K_j⟩被权重衰减

a_i : j^× = a_i⋯a_j + 1

这可以解释为基于位置i和j之间距离的“折扣系数” ^[5]。在其注意力形式中，这种依赖于输入的位置掩模可以被解释为编码Mamba“选择性”的关键因素。

3.2 SSD框架1：结构化矩阵变换

本节探讨了状态空间模型作为序列变换的不同视角，并概述了此类映射的属性和算法。本节的主要结果是关于状态空间模型与一类称为半可分矩阵的结构化矩阵之间的等价性。

3.2.1 矩阵变换

多序列模型，即序列变换X ∈ ℝ^(T, P) ↦ Y ∈ ℝ^(T, P)，可以写成单个矩阵乘法Y = M(X) ⋅ M的形式，其中M是一个矩阵，可以本身取决于X。称之为矩阵序列变换，简称矩阵变换。在文献中，序列变换也被称为“序列混合器”或“令牌混合器”，矩阵序列变换也被称为“矩阵混合器”。这样的例子有很多，它们通过M 矩阵的结构来区分。事实上的例子是自注意力本身，其中M = softmax(QK^⊤) 是注意力矩阵。其他示例包括 MLP-Mixer,FNet,Monarch Mixer

根据定义，h₀ = B₀x₀。通过归纳，

乘以 C_t 得到 y_t，并将方程在 t ∈ [T] 上矢量化，推导出 SSM 的矩阵变换形式。

SSM可以写成矩阵变换

Y = SSM(A, B, C)(X) = MX

其中M_ij = 0当i < j时（即它是下三角形），否则

M_ij = C_i^⊤A_i : j^×B_j ≔ C_i^⊤A_i⋯A_j + 1B_j

画出来，这个矩阵看起来像

(Matrix Transformation Representation of State Space Models)

3.2.2 半可分离矩阵(Semiseparable Matrices)

M 是称为半可分矩阵的一类矩阵的特殊表示。半可分矩阵是一种基本矩阵结构。

如果下三角部分（即对角线上或对角线下）包含的每个子矩阵的秩最多为 N，则 (下三角) 矩阵 M 是 N-半可分的。称 N 为半可分矩阵的阶或秩。半可分离矩阵有许多结构化表示，包括分层半可分离 (HSS)、顺序半可分离 (SSS) 和 Bruhat 形式^[7]。

定义算子 SSS 使得 M = SSS(A_0 : T, B_0 : T, C_0 : T)。半可分矩阵的一个基本结果是，它们与具有 SSS 表示的矩阵完全等价。具有表示上述公式的 N-SSS 矩阵 M 是 N-半可分的。

考虑任何非对角块 M_{i : i^′, j^′ : j}，其中 i^′ > i ≥ j > j^′。这具有明确的秩-N 分解为

每个 N-半可分矩阵都有一个 N-SSS 表示。使用 N-SS 来指代 SSS 形式的 N-半可分矩阵。

3.2.3 1-半可分矩阵：标量 SSM 递归

1-SS 矩阵的特殊情况。在这种情况下，C_i 和 B_j 是标量，1-SS 矩阵的基本表示是 M_ij = a_i : j或

(1 − semiseparable (1 − SS) matrix)

1-SS 矩阵的重要性在于它们等价于标量递归的最小形式——状态维度 N = 1 且无 (B, C) 投影的退化 SSM 的情况。请注意，乘法 y = Mx 可以通过递归计算

将矩阵乘以 1-SS 矩阵称为标量 SSM 递归 或 cumprodsum（累积乘积和；累积乘积和累积和的泛化）运算符。作为递归的基本形式，乘以 1-SS 矩阵非常重要作为主要算法的构建块。

3.2.4 状态空间模型是半可分的矩阵

状态空间模型变换 y = SSM(A, B, C)(x) 具有状态大小 N，与顺序半可分表示 y = SSS(A, B, C) ⋅ x 中 N-SS 矩阵的矩阵乘法相同。

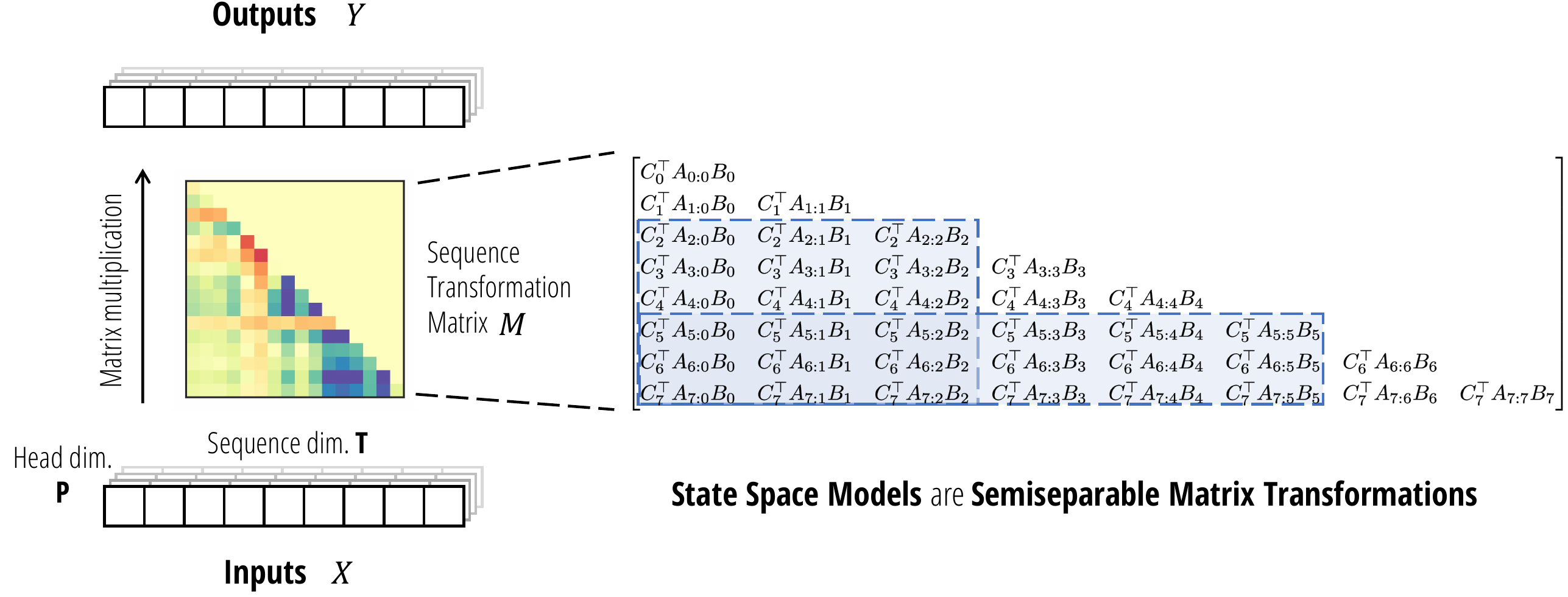
状态空间模型是半可分矩阵作为序列变换，状态空间模型可以表示为作用于序列维度 T 的矩阵变换 M ∈ ℝ^(T, T)，头部中的每个通道共享相同的矩阵 (左)。该矩阵是一个半可分矩阵 (右)，它是一个秩结构矩阵，其中对角线上下的每个子矩阵 (蓝色) 的秩最多为 N，等于 SSM 的状态维度。

3.2.5 通过结构化矩阵算法计算状态空间模型

半可分矩阵（即秩结构矩阵）是一种经典的结构化矩阵：

它们具有压缩表示，例如 SSS 形式，其仅具有 O(T) 而不是 O(T²) 参数。
它们具有直接在压缩表示上运行的快速算法。

大小为 T 的 N-SS 矩阵可以用 O(NT) 个参数表示，并且在时间和空间上具有矩阵向量乘法 O(NT)。

张量收缩算法：其中维度 S 等于 T收缩符号需要不同的符号。

这里，L ∈ ℝ^(T, T) 定义为 1SS(A)，或者换句话说，对于 i ∈ [N]，L_{0 : T, 0 : T} = 1SS(A_0 : T)。该算法涉及三个步骤，对于

扩展输入 X 乘以输入矩阵 B
展开独立标量 SSM 递归第二步
收缩隐藏状态 H 乘以输出矩阵 C

任何状态空间模型，其状态大小为 N，序列长度为 T，都可以在时间内计算出 O(TN)（不考虑潜在的预处理）。

3.3 SSD框架2：结构化注意力

节的主要结果是基于张量收缩的线性注意力的简单证明，以及在SMA中对结构化掩蔽注意力的广义抽象。

masked-attention为注意力变体建立了框架，特别关注内核注意力和掩蔽内核注意力。
linear-attention提供了的第一个主要注意力结果，即通过张量收缩的视角对线性注意力的简单证明。
structured-attention定义了结构化掩蔽注意力，这是通过结构化矩阵对先前注意力变体的概括。

3.3.1 Kernel Attention

将注意力定义为一个函数

(Q^(T, N), K^(S, N), V^(S, P)) ↦ Y^(T, P))

由成对矩阵乘法给出

Y = (QK^⊤) ⋅ V

将P = N视为头部尺寸；从技术上讲，请注意V头部尺寸P可以与QK头部尺寸N不同。将T视为目标序列维度，将S视为源序列维度。给这两个轴赋予不同的名称将使数学更加清晰，并且还涵盖更一般的注意力形式，例如交叉注意力，其中源和目标是具有不同长度的单独序列。然而，将假设自注意力设置为S = T。

通常的注意力形式Y = f(QK^⊤) ⋅ V（例如，其中f是softmax函数）可以，对于基本上所有函数f并且最多一些额外的处理，例如易于处理的行归一化，对于某些适当的特征图ψ（可能是无限维的）可写为Y = ψ(Q)ψ(K)^⊤ ⋅ V 。在这种情况下，可以简单地重新定义Q ← ψ(Q)并将N定义为注意力内核的特征维度。例如，Softmax 注意力可以用表示指数核的特定无限维特征图(N = ∞)来表示。

限制ψ有限的情况，这有时称为内核注意力。当序列长度T增长并且特征维度N较小时 - 通常，在ψ很简单（例如元素变换）的情况下，因此N是恒定的——那么注意力成本可以从T中的二次减少到线性。这是通过简单地以不同的顺序计算矩阵乘法得出的

Y = Q ⋅ (K^⊤V)

线性化注意力的最常见方法通常被视为矩阵乘法关联性的结果。

3.3.2 (Causal) Linear Attention

然而，一旦基本核注意力稍加修改，就不能再直接使用矩阵乘法的结合性了。

Linear Attention (LA)框架^[6]。表明它仍然可以扩展到将因果关系纳入注意力的重要情况，用于自回归设置（例如语言建模）。

更明确地了解它是如何工作的。因果线性注意力的二次形式是

Y = (L ∘ QK^⊤)V

其中

是因果掩模矩阵。

一旦L掩码合并到中，就不能再直接应用矩阵关联性！这是最初的线性注意力论文解决的问题。他们表明相当于一种不同的形式，避免了二次QK^⊤注意力矩阵的具体化，并且具有线性时间复杂度

Y = Q ⋅ cumsum(K^⊤V)

线性注意力中累积和的出现完全等同于因果掩码L作为矩阵乘法编码累积和的事实：

3.3.2.1 线性注意力的张量收缩(Tensor Contraction)证明

用张量收缩或 einsum 表示法非常明确地写出线性注意力的二次形式，并带有形状注释：

(Structured Masked Attention − Quadratic Form)

通过这个符号，可以注意到这个收缩序列可以写成一个单一的四向收缩

Y = contract(TN, SN, SP, TS → TP)(Q, K, V, L)

最后，它可以用任何其他收缩排序来计算。特别是，可以对顺序V, K, L, Q而不是Q, K, L, V执行成对归约

(Structured Masked Attention − Linear Form)

现在关键的观察是的第二行只是与L的矩阵乘法，可以通过累积和来计算。它的美妙之处在于不必写出单个求和，它被抽象为与L结构相结合的张量收缩。这表明线性注意力的效率可以变得更加普遍。

3.3.3 Structured Masked Attention

从掩蔽注意力的张量收缩角度来看，原始线性注意力的关键在于矩阵向量乘以因果掩码等同于累积和运算符。注意力掩码没有理由必须全部为 1。线性注意力要快速运行，只需要 L 是一个结构化矩阵，根据定义，结构化矩阵具有快速矩阵乘法。具体来说，可以使用任何具有次二次（理想情况下为线性）矩阵向量乘法的掩码矩阵 L，通过加速瓶颈方程，它将具有与标准线性注意力相同的复杂性。

结构化掩蔽注意力 (SMA)（或简称为结构化注意力）定义为对查询/键/值 Q, K, V 以及任何结构化矩阵 L（即具有次二次矩阵乘法）的函数，通过 4 向张量收缩

SMA二次模式算法是由定义的成对收缩序列，对应于标准（掩蔽）注意力计算。

SMA线性模式算法是由定义的成对收缩序列，其中步骤2通过次二次结构化矩阵乘法进行优化。

可以将结构化掩蔽注意力实例化为任何给定的矩阵结构类。一些示例包括：

线性注意力使用因果掩码。
RetNet 使用衰减掩码 L_ij = γ^i − j ⋅ 𝕀[j ≥ i]，其中衰减因子 γ ∈ [0, 1]。
对于某些可学习（或输入相关）参数集 α ∈ ℝ^T，衰减掩码可以推广到 Toeplitz 矩阵 L_ij = α_i − j。这可以解释为一种相对位置编码的形式，让人想起 AliBi 等其他方法，但采用乘法而不是加法。
另一种变体可以使用傅里叶矩阵 L_ij = ω^ij/T 以不同的方式对位置结构进行编码。

在ssd中，考虑半可分离 SMA，它定义了的主要 SSD 模型。

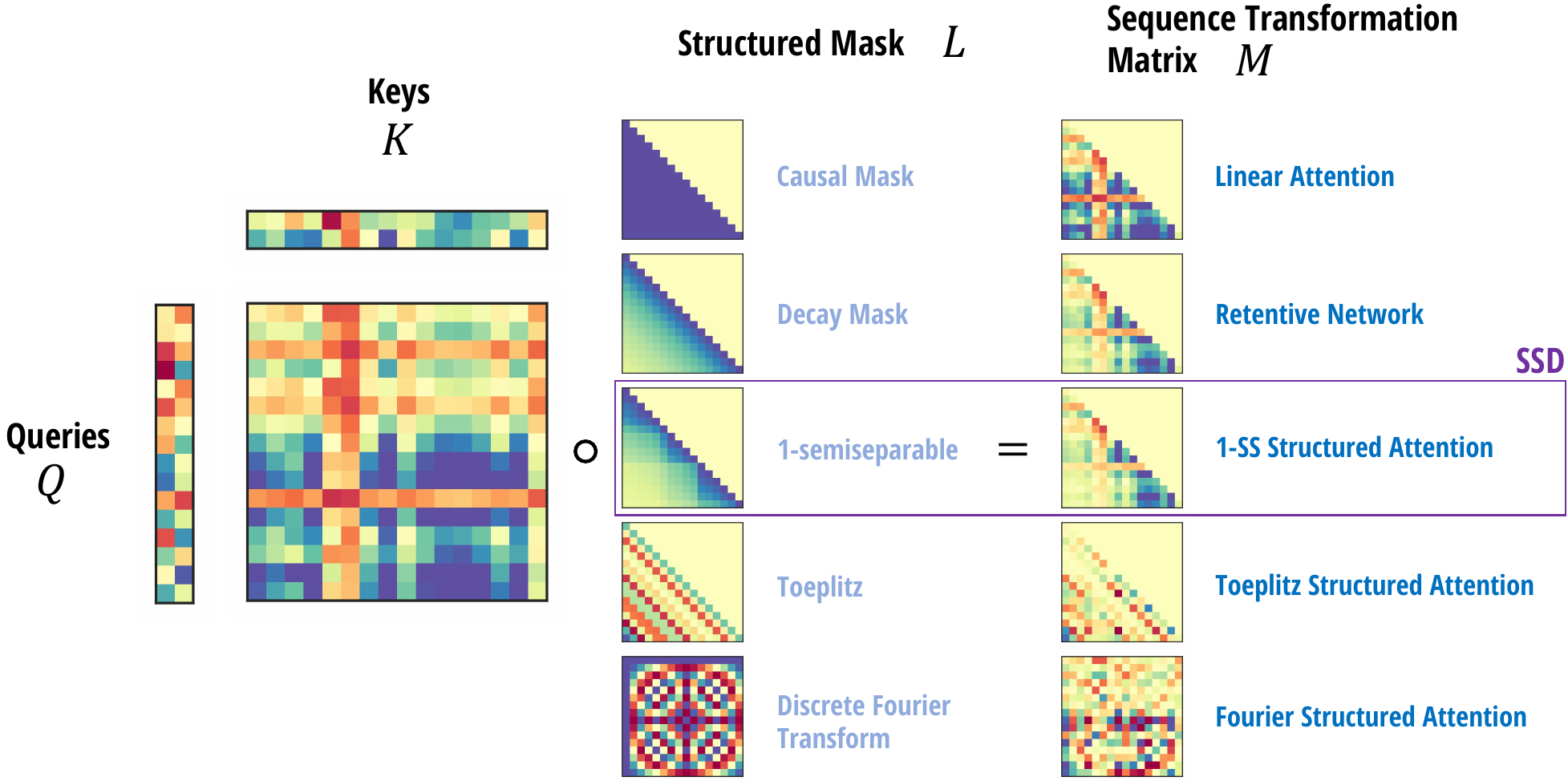
SMA 为任何结构化矩阵 L 构建了一个掩蔽注意力矩阵 M = QK^⊤ ∘ L，它定义了一个矩阵序列变换 Y = MV。SMA 的所有实例都具有由不同收缩顺序引起的对偶次二次形式，并结合了有效的结构化矩阵乘以 L。之前的示例包括线性注意力~RetNet。除了本文的重点 SSD（1-半可分离 SMA）之外，结构化注意力的许多其他潜在实例也是可能的。

掩盖注意力的双重形式

标准（掩蔽核）注意力机制通常被混为一谈，既是函数又是算法。区分这种区别可以清晰地理解注意力机制的不同变体。

将 maskedtention 视为一个特定的function。
标准 quadratictention 计算可视为一种计算该函数的algorithm。
Lineartention是计算相同函数的另一种算法。

此外，在这种情况下

掩蔽注意力函数仅仅是四个项的特定收缩。
二次和线性注意力算法仅仅是执行收缩的两种不同顺序。

众所周知，收缩顺序会对计算复杂度造成巨大影响，从而导致二次与线性分裂。正如状态空间模型是一种可以通过多种方式计算的变换，具有对偶二次与线性形式，线性注意力具有由两个收缩顺序产生的类似对偶性。

3.4 State Space Duality

在attention中，定义了结构化状态空间模型和结构化注意力，讨论了它们的属性，并表明它们都有二次算法和线性算法。本节将它们联系在一起。主要结果是表明结构化状态空间模型的一个特定情况与结构化注意力的一个特定情况相吻合，并且线性时间 SSM 算法和二次时间核注意力算法是彼此的对偶形式。

3.4.1 标量恒等结构状态空间模型

现在让考虑 A_i 只是一个标量的情况；换句话说，结构化 SSM 的实例，其中 A 矩阵是极其结构化的：对于标量 a 和单位矩阵 I，A = aI。然后可以重新排列

这可以矢量化为

其中 B, C ∈ ℝ^(T, N)。使用此公式，完整输出 Y = MX 的计算方式精确为

其中 S = T。但这与 masked kerneltention 的原始定义完全相同.

因此，通过具体化半可分矩阵 M 并执行二次矩阵向量乘法来天真地计算标量结构化 SSM —— 与二次掩蔽核注意力完全相同。

3.4.2 1-半可分离结构化掩蔽注意力

1-SS SMA（具有 1-半可分结构矩阵 L 的掩蔽注意力）是对角 SSM的一个特例，其中对角矩阵是恒等矩阵的标量倍数。

1-半可分离结构化注意力是 SMA 最重要的情况，因为它：

具有输入相关递归的线性注意力的自然泛化。
一般半可分离注意力的最简单情况，相当于有效的自回归注意力。
对角状态空间模型的特殊情况。

3.4.3 结构化状态空间对偶 (SSD)

总结一下结果：

结构化状态空间模型通常通过线性时间递归定义。但是，通过扩展表征其线性序列到序列变换的矩阵公式，可以得出二次形式。
注意力变体是通过二次时间成对交互定义的模型。但是，通过将其视为四向张量收缩并以不同的顺序减少，可以得出线性形式。
每一个的自然特例—— 更准确地说，在 A 矩阵上具有标量恒等结构的状态空间模型，以及在其 L 掩码上具有 1 半可分离结构的结构化掩码注意力 ——是彼此的对偶，具有完全相同的线性和二次形式。

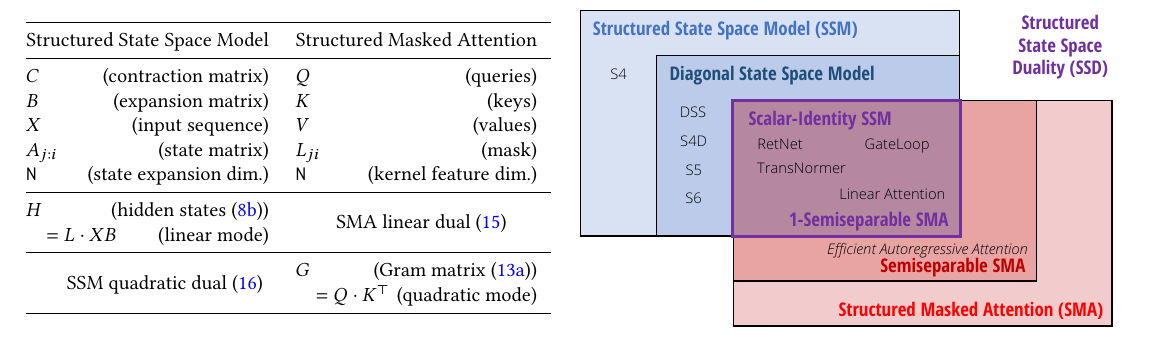
结构化状态空间对偶

状态空间对偶描述了状态空间模型和掩蔽注意力之间的密切关系。(左) 一般 SSM 和 SMA 都具有线性和二次形式，符号上有直接类似物。(右) SSM 和 SMA 在一大类状态空间对偶模型(SSD) 中相交，这些模型将许多序列模型作为特例捕获。

3.5 SSD 模型的硬件高效算法

首先，将矩阵 M 划分为一个个子矩阵网格，每个子矩阵的大小为 Q × Q，其中块大小为 Q。请注意，根据半可分矩阵的定义性质，非对角块的秩较低。请注意，即使分区大小不同，块分解仍然有效，例如如果，但为了简单起见，假设偶数可分性。

最简单的例子是，T = 9 分解为长度为 Q = 3 的块。阴影单元是半可分矩阵非对角线块的低秩分解。

从这里可以将问题简化为这两个部分。这也可以解释为将“块”y_{jQ : (j + 1)Q}的输出分为两个部分：块x_{jQ : (j + 1)Q}内的输入的影响，以及块x_0 : jQ之前的输入的影响。

3.5.1 Diagonal Blocks

对角块很容易处理，因为它们只是较小规模的自相似问题。第 j 个块表示计算范围 R = jQ : (j + 1)Q = (jQ, jQ + 1, …, jQ + Q − 1) 的答案 SSM(A_R, B_R, C_R)(x_R)。关键是可以使用任何所需的方法来计算此块。特别是，对于小块长度 Q，使用对偶二次 SMA 形式可以更有效地计算此问题。此外，可以并行计算块。

这些子问题可以解释为：假设初始状态（对于块而言）为 0，则每个块的输出是多少。换句话说，对于块 j，这仅考虑块输入 x_{jQ : (j + 1)Q} 即可计算正确的输出。

3.5.2 Low-Rank Blocks

低秩分解由 3 个项组成，因此计算有 3 个部分。在此分解中，将使用术语

像这样的项被称为右因子或 B-block-factors。
像 A_5 : 2 这样的项被称为中心因子或 A-block-factors。
像这样的项被称为左因子或 C-block-factors。

Right Factors.

此步骤计算低秩分解的右 B 个块因子的乘积。请注意，对于每个块，这是一个 (N, Q) 乘以 (Q, P) 矩阵乘法，其中 N 是状态维度，P 是头部维度。结果是每个块的 (N, P) 张量，其维度与扩展隐藏状态 h 相同。

这可以解释为：假设初始状态（对于块）为 0，则每个块的最终状态是什么。换句话说，假设 x_0 : jQ = 0，计算 h_{jQ + Q − 1}。

enter Factors.

此步骤计算低秩分解中的中心 A 块因子项的影响。在上一步中，每个块的最终状态具有总体形状 (T/Q, N, P)。现在将其乘以由 A_{2Q − 1 : Q − 1}^×, A_{3Q − 1 : 2Q − 1}^×, …, A_{T − 1 : T − Q − 1}^× 生成的 1-SS 矩阵。

此步骤可以通过任何计算 1-SS 乘法的算法（也称为标量 SSM 扫描或运算符）来计算。

这可以解释为：每个块的实际最终状态是什么 考虑到所有先前的输入；换句话说，这将计算真实隐藏状态 h_jQ，其中考虑了所有 x_{0 : (j + 1)Q}。

Left Factors.

此步骤计算低秩分解的左 C 个块因子的乘积。对于每个块，这可以用矩阵乘法contract(QN, NP → QP) 表示。

这可以解释为：每个块的输出是多少 考虑到正确的初始状态 h_jQ − 1，假设输入 x_{jQ : (j + 1)Q} 为 0。换句话说，对于块 j，这仅考虑先前的输入 x_0 : jQ 即可计算正确的输出。

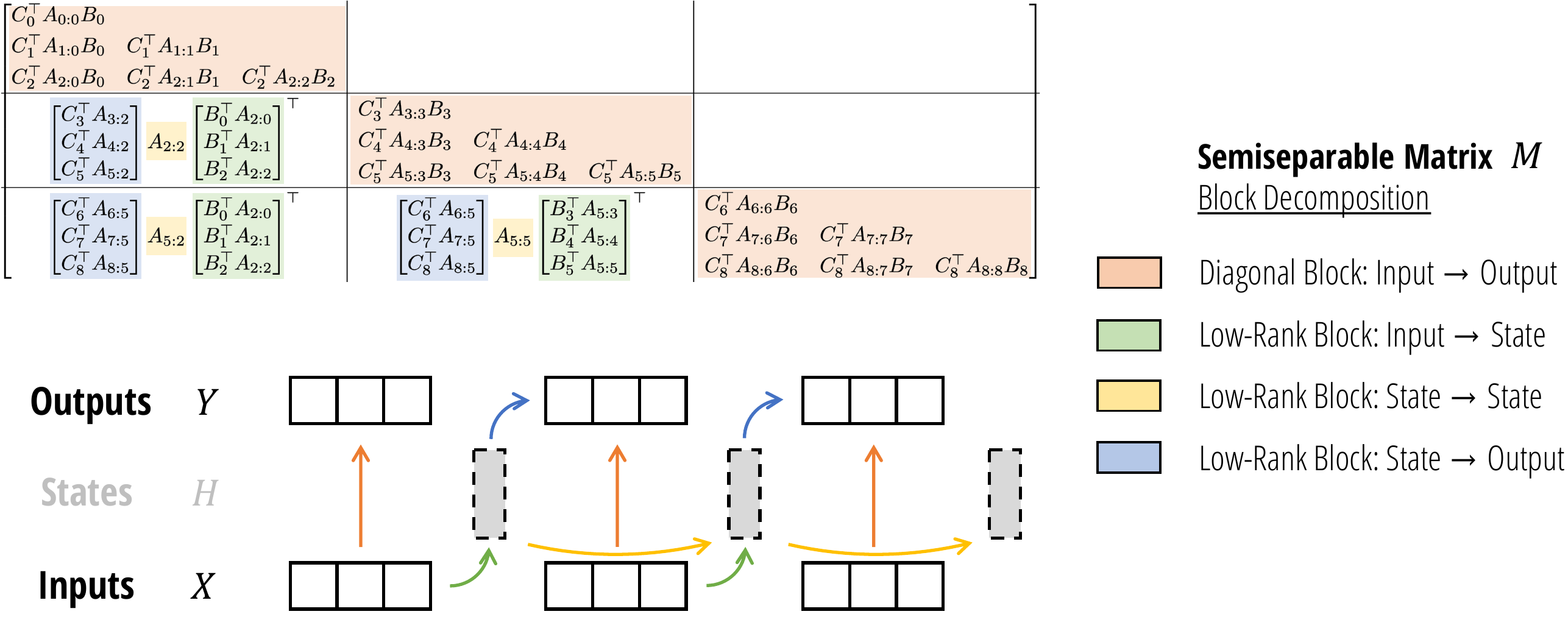
SSD算法：分块矩阵分解 离散化；可以随心所欲地计算这个乘法；特别是，使用 SSD 的二次（类似注意力）形式。

（绿色）总共只有 T/Q个不同的绿色块，因为其中许多是共享的。这些可以使用批处理 matmul 来计算。
（黄色）请注意，黄色项本身形成一个 1-半可分离矩阵；换句话说，这一步相当于SSM扫描（在某些修改的A因素上）！
（蓝色）与绿色类似，这些可以使用批处理 matmul 来计算。

SSD 算法：分块和状态传递

该算法的另一种解释涉及推理 SSM 如何对实际序列进行操作。首先将输入序列分割成大小为Q的块（或块）。步骤就有解释了 1. 块内输出：计算每个块的本地输出（假设（块的）初始状态为 0，每个块的输出是多少？） 2. 块状态：计算每个块的最终状态（假设（块的）初始状态为 0，每个块的最终状态是什么？） 3. 通过状态：计算所有块的最终状态的递归 - 使用任何所需的算法，例如并行或顺序扫描（考虑到所有先前的输入，每个块的实际最终状态是什么？） 4. 输出状态：对于每个块，给定其真实的初始状态（在步骤 3 中计算），计算初始状态对输出的贡献

不管怎样，大多数算法（步骤 1、2 和 4）利用了 matmuls（以及张量核心），并且也可以完全并行计算！只有第 3 步需要扫描，但它的操作序列要短得多，并且通常只需要整个算法时间的一小部分。

3.5.3 Computational Cost

定义符号 BMM(B, M, N, K) 来定义批量矩阵乘法 contract(MK, KN → MN)，批量维度为 B。从这个符号可以推断出效率的三个方面：

计算成本：总计 O(BMNK) FLOPs。
内存成本：总计 O(B(MK + KN + MN)) 空间。
并行化：更大的 M、N、K 项可以利用现代加速器上的专门矩阵乘法单元。

def segsum(x):
    """Naive segment sum calculation. exp(segsum(A)) produces a 1-SS matrix,
       which is equivalent to a scalar SSM."""
    T = x.size(-1)
    x_cumsum = torch.cumsum(x, dim=-1)
    x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
    mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
    x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
    return x_segsum

def ssd(X, A, B, C, block_len=64, initial_states=None):
    """
    Arguments:
        X: (batch, length, n_heads, d_head)
        A: (batch, length, n_heads)
        B: (batch, length, n_heads, d_state)
        C: (batch, length, n_heads, d_state)
    Return:
        Y: (batch, length, n_heads, d_head)
    """
    assert X.dtype == A.dtype == B.dtype == C.dtype
    assert X.shape[1] % block_len == 0

    # Rearrange into blocks/chunks
    X, A, B, C = [rearrange(x, "b (c l) ... -> b c l ...", l=block_len) for x in (X, A, B, C)]

    A = rearrange(A, "b c l h -> b h c l")
    A_cumsum = torch.cumsum(A, dim=-1)

    # 1. Compute the output for each intra-chunk (diagonal blocks)
    L = torch.exp(segsum(A))
    Y_diag  = torch.einsum("bclhn,bcshn,bhcls,bcshp->bclhp", C, B, L, X)

    # 2. Compute the state for each intra-chunk
    # (right term of low-rank factorization of off-diagonal blocks; B terms)
    decay_states = torch.exp((A_cumsum[:, :, :, -1:] - A_cumsum))
    states = torch.einsum("bclhn,bhcl,bclhp->bchpn", B, decay_states, X)

    # 3. Compute the inter-chunk SSM recurrence; produces correct SSM states at chunk boundaries
    # (middle term of factorization of off-diag blocks; A terms)
    if initial_states is None:
        initial_states = torch.zeros_like(states[:, :1])
    states = torch.cat([initial_states, states], dim=1)
    decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0))))
    new_states = torch.einsum("bhzc,bchpn->bzhpn", decay_chunk, states)
    states, final_state = new_states[:, :-1], new_states[:, -1]

    # 4. Compute state -> output conversion per chunk
    # (left term of low-rank factorization of off-diagonal blocks; C terms)
    state_decay_out = torch.exp(A_cumsum)
    Y_off = torch.einsum('bclhn,bchpn,bhcl->bclhp', C, states, state_decay_out)

    # Add output of intra-chunk and inter-chunk terms (diagonal and off-diagonal blocks)
    Y = rearrange(Y_diag+Y_off, "b c l h p -> b (c l) h p")
    return Y, final_state

Center Blocks.

二次 SMA 计算的成本包括三个步骤：

计算核矩阵 C^⊤B，其成本为 BMM(T/Q, Q, Q, N)。
乘以掩码矩阵，这是对形状为 (T/Q, Q, Q) 的张量的元素运算。
乘以 X 值，其成本为 BMM(T/Q, Q, P, N)

Low-Rank Blocks: Right Factors.

此步骤是长度为 T/Q 的标量 SSM 扫描（或 1-SS 乘法），在 (N, P) 个独立通道上进行。此扫描的工作量为 TNP/Q，与其他因素相比可以忽略不计。

请注意，由于阻塞将序列长度从 T 缩短为 T/Q，此扫描的成本比纯 SSM 扫描（例如 Mamba 的选择性扫描）小 Q 倍。因此，在大多数问题长度上，其他算法scan可能更有效或更容易实现，而不会出现明显的减速。例如，通过 1-SS 矩阵乘法实现的简单实现成本为 BMM(1, T/Q, NP, T/Q)，这比简单的递归/扫描实现更容易实现，而且效率更高。

Low-Rank Blocks: Left Factors.

此步骤是单矩阵乘法，成本为 BMM(T/Q, Q, P, N)。

Total Cost.

如果设置 N = P = Q（换句话说，状态维度、头部维度和块长度相等），那么上述所有 BMM 项都变为 BMM(T/N, N, N, N)。其计算特性如下：

总 FLOP 数为 O(TN²)。
总内存为 O(TN)。
工作主要包括形状为 (N, N) 的矩阵的矩阵乘法。

请注意，内存消耗很紧；输入和输出 x, y 的形状为 (T, P) = (T, N)。同时，Flop 计数反映了额外的 N 因子，这是自回归状态大小产生的成本，并且是所有模型所共有的。

除了 matmuls 之外，还有一个标量 SSM 扫描，扫描 NP = N² 个特征和序列长度 T/Q。这花费了 O(T/QN²) FLOP 和 O(log (T/Q)) 深度。虽然它不使用矩阵乘法，但它仍然是可并行的，并且与其他步骤相比，完成的总工作量可以忽略不计；这在 GPU 实现中成本可以忽略不计。

Comparison to Pure SSM and Attention Models.

二次注意力机制也非常高效地利用了硬件，因为它只利用了矩阵乘法，但总 FLOP 为 T²N。它在训练和推理时计算速度较慢，这可以直接看作是状态规模较大的结果——标准注意力机制的状态规模会随序列长度 T 而变化，因为它会缓存历史记录，而不会压缩状态。

线性 SSM 的总 FLOP 为 TNP = TN²，与 SSD 相同。然而，简单的实现需要状态扩展来实现额外的内存，以及标量运算，它不会利用矩阵乘法。

	Attention	SSM	SSD
State size	`T`	N	N
Training FLOPs	`T`²`N`	TN²	TN²
Inference FLOPs	`TN`	N²	N²
(Naive) memory	`T`²	`TN`²	TN
Matrix multiplication	✓		✓

许多其他矩阵分解都是可能的（例如，了解通过不同结构化矩阵分解进行 1-SS 乘法的算法概要）这可能导致更多 SSD 算法，这些算法可能更适合其他专门设置。更广泛地说，除了使用的 SSS 形式之外，半可分矩阵还有丰富的文献和更多的表示形式，甚至可能存在更高效的算法。

3.5.4 Stability

尝试 1：CUMPRODS 比率

第一次天真的尝试可能是注意到该矩阵的条目是累积乘积

然而，这会遇到严重的数字问题，因为这些乘积可能变得非常小(想象一下a_t ≈ 0.9并为其提供数千个序列长度T)

修复 1：段求和 ( SEGSUM ) 运算

第二次尝试是在日志空间中完成所有这些，因为所有a_t都是正数；因此产品变成了附加项，用 cumsum代替要处理的 cumprod 。然后，为了计算 1-SS 矩阵，只需计算每个段[i : j]的和。将其称为段和 (segsum) 原语，类似于累积和 (cumsum)。

尝试 2：CUMSUMS 的差异

再次执行此操作的明显方法是使用与上面相同的想法，但是在日志空间中

a_i : j^× = exp (log a_i + ⋯ + log a_j − 1) = ((log a)_i : T⁺ − (log a)_j : T⁺)

沿时间轴计算a的单个累积和，然后计算所有成对差异。在代码中，可以这样做

def segsum_unstable(x):
    """Naive segment sum calculation."""
    T = x.size(-1)
    x_cumsum = torch.cumsum(x, dim=-1)
    x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
    mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
    x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
    return x_segsum离散化

（然后 1-半可分离矩阵就是该输出的指数）。和/差比乘积/商稳定得多，所以这应该可行——对吧？

修复 2：删除所有减法

不幸的是，事实证明这仍然行不通。这个 1-SS 矩阵的值大致代表了 SSM 动态，它对a_t的这些值非常敏感，因此必须非常精确。即使在日志空间中，这些累积和也可能相当大，在相减时会导致灾难性的抵消。因此，确实必须找到一种方法来仅通过加法来计算这个矩阵，同时仍然对所有内容进行矢量化

尝试 3：稳定 SEGSUM

这引出了参考 SSD 代码中的辅助函数。找到了一种方法来使用一批独立的累加值，无需减法即可立即产生正确的答案，而不是计算单个累加值然后进行减法。

这些细节很重要！如果没有正确实现这些原语，基本 SSD 算法会在训练期间立即生成 NaN（即使使用 FP32）。

离散化

这种结构化状态空间模型的谱系是从 S4 及其前身发展而来的，它们被视为连续时间系统。然而，在 Mamba 中，不再真正认为 SSM 是连续的。事实上，正如原始论文的讨论（第 5 节）中提到的，Mamba 在建模不同类型的数据时与 S4 进行了权衡：

S4 是一种连续时间模型，擅长对连续数据进行建模，例如感知信号，例如音频波形和像素级视觉。
Mamba 是一种离散时间模型，擅长对离散数据进行建模，例如标记化数据，例如语言。

然而，Mamba 的参数化仍然使用与先前结构化 SSM 相同的离散化步骤，其中有另一个参数Δ正在建模。这样做是因为离散化步骤有其他副作用，例如正确标准化激活这对于性能很重要。

先前关于结构化 SSM 的理论的初始化和参数化仍然是开箱即用的，那么为什么要修复没有损坏的东西呢？

尽管如此，离散化步骤对于 Mamba 来说并不是真正必要的。在 Mamba-2 论文中，选择直接使用“离散参数” A和B，在之前的所有结构化 SSM 论文（包括 Mamba-1）中均表示为(Ā, B̄)并通过附加转换定义

这不会造成任何问题：要使用连续 SSM 参数化，只需在插入上面的 SSD 代码之前通过上述公式转换参数即可。

在完整的 Mamba-2 代码中，还保留了与 Mamba 相同的参数化和离散化步骤——同样，为什么要修复没有损坏的东西？——但假设“以离散为中心”的变体（例如 LRU和 Griffin 的伽玛归一化）应该同样有效。

### 3.6 Mamba-2 Architecture

通过连接 SSM 和注意力机制，SSD 框架能够为两者开发一个共享的词汇表和技术库。在本节中，将讨论一些使用最初为 Transformers 开发的想法来理解和修改 SSD 层的示例。

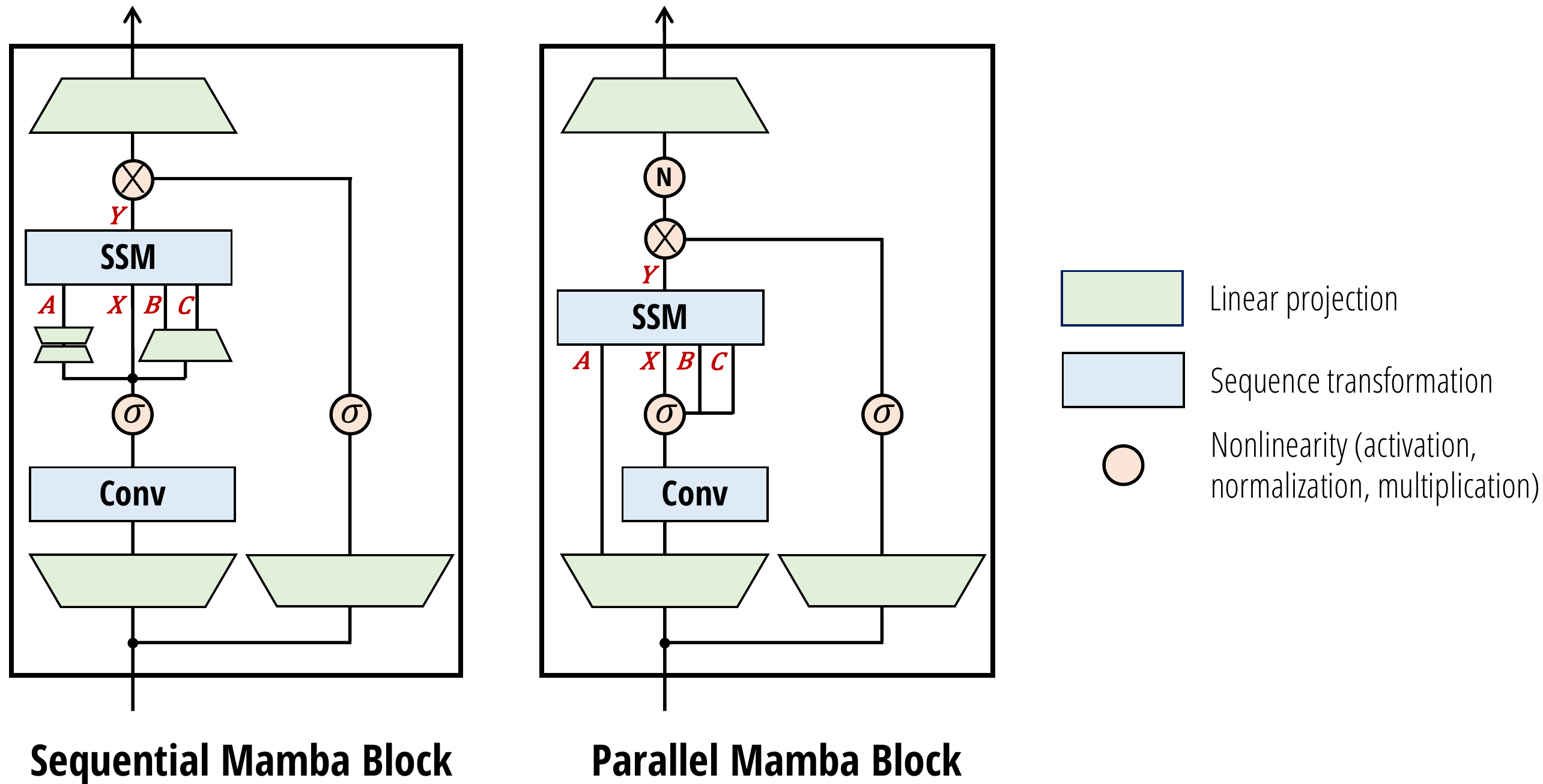
Mamba-2 块通过删除连续线性投影简化了 Mamba 块；SSM 参数 A、B、C 在块的开头生成，而不是作为 SSM 输入 X 的函数。像在 NormFormer中一样添加了一个额外的规范化层，以提高稳定性。B 和 C 投影只有一个在 X 个头之间共享的头，类似于多值注意力 (MVA)。

3.6.1 Block Design

首先讨论对独立于内部序列混合层（即核心 SSD 层之外）的神经网络块的修改。

Parallel Parameter Projections.

Mamba-1 的动机是 SSM 中心观点其中选择性 SSM 层被视为从 X ↦ Y 的映射。SSM 参数 A、B、C 被视为辅助参数，是 SSM 输入 X 的函数。因此，定义 (A, B, C) 的线性投影发生在初始线性投影之后，以创建 X。

在 Mamba-2 中，SSD 层被视为从 A、X、B、C ↦ Y 的映射。因此，在块开头与单个投影并行生成 A、X、B、C 是有意义的。请注意与标准注意架构的类比，其中 X、B、C 对应于并行创建的 Q、K、V 投影。

请注意，通过使用标准 Megatron 分片模式，对 SSM 的 A, B, C, X 输入采用并行投影会稍微减少参数，更重要的是，它更适合较大模型的张量并行性。

Extra Normalization.

在初步实验中，发现较大的模型容易出现不稳定性。能够通过在最终输出投影之前向块添加额外的规范化层（例如 LayerNorm、GroupNorm 或 RMSNorm）来缓解这种情况。这种规范化的使用与 NormFormer 架构最直接相关，该架构还在 MLP 和 MHA 块的末尾添加了规范化层。

还注意到，这种变化类似于从线性注意观点得出的与 Mamba-2 相关的其他最新模型。原始线性注意公式通过分母项进行规范化，该分母项模拟标准注意中 softmax 函数的规范化。TransNormerLLM和 RetNet发现这种规范化是不稳定的，并在线性注意层之后添加了额外的 LayerNorm 或 GroupNorm。额外规范化层与这些略有不同，它出现在乘法门分支之后而不是之前。

3.6.2 Multihead Patterns for Sequence Transformations

回想一下，SSM 被定义为序列变换其中：

A, B, C 参数具有状态维度 N。
它们定义了一个序列变换 ℝ^T → ℝ^T，例如可以表示为矩阵 M ∈ ℝ^(T, T)。
此变换对输入序列 X ∈ ℝ^(T, P) 进行操作，独立于 P 轴。

可以将其视为定义序列变换的一个head。多头序列变换由 H 个独立头组成，总模型维度为 D = d_model。参数可能跨头绑定，从而产生头模式。

状态大小 N 和头部维度 P 分别类似于注意力机制的 QK 头部维度和 V 头部维度。就像在现代 Transformer 架构中一样，在 Mamba-2 中，通常选择这些常数约为 64 或 128；当模型维度 D 增加时，增加头部数量，同时保持头部维度 N 和 P 不变。为了描述如何做到这一点，可以迁移和概括多头注意力机制中的思想，为 SSM 或任何一般序列变换定义类似的模式。

Multihead SSM (MHS) / Multihead Attention (MHA) Pattern.

经典的 MHA 模式假设头部维度 P 除以模型维度 D。头部数量定义为 H = D/P。然后，通过创建每个参数的 H 个独立副本来创建核心序列转换的 H 个副本。请注意，虽然 MHA 模式最初是为注意序列转换而描述的，但它可以应用于与sequence-transformation兼容的任何事物。例如，多头 SSD 层将接受具有符合方程Multi-head SSM形状的输入，其中 SSD 算法在 H = n_heads 维度上广播。

Multi-contract SSM (MCS) / Multi-query Attention (MQA) Pattern.

多查询注意力是一种巧妙的注意力优化方法，可以显著提高自回归推理的速度，它依赖于缓存 K 和 V 张量。这种技术只是避免给 K 和 V 额外的头部维度，或者换句话说，在 Q 的所有头部上广播单个 (K, V) 头部。

使用状态空间对偶，可以将 MQA 的等效 SSM 版本定义为方程Multi-contract SSM。这里，X 和 B（注意力的 V 和 K 的 SSM 类似物）在 H 个头部之间共享。也称之为多契约 SSM (MCS)头部模式，因为控制 SSM 状态收缩的 C 参数每个头部都有独立的副本。

可以类似地定义一个多键注意 (MKA) 或多扩展 SSM (MES) 头部模式，其中 B（控制 SSM 扩展）是每个头部独立的，而 C 和 X 则在各个头部之间共享。

Multi-input SSM (MIS) / Multi-value Attention (MVA) Pattern.

虽然 MQA 因其 KV 缓存而适合用于注意力机制，但它并不是 SSM 的自然选择。在 Mamba 中，X 被视为 SSM 的主要输入，因此 B 和 C 是跨输入通道共享的参数。Multi-input SSM方程中定义了多输入 SSM (MIS) 模式的新多值注意力 (MVA)，它可以再次应用于任何序列转换，例如 SSD。

有了这个词汇表，可以更准确地描述原始的 Mamba 架构。

Mamba 架构的选择性 SSM（S6）层可以被视为具有:

头部维度 P = 1：每个通道都有独立的 SSM 动态 A。
多输入 SSM (MIS) 或 多值注意 (MVA) 头部结构：B, C 矩阵（对应注意对偶中的 K, Q）在输入 X（对应注意中的 V）的所有通道之间共享。

当应用于 SSD 时，还可以消除这些头部模式变体。有趣的是，尽管在参数数量和总状态维度方面受到控制，但下游性能仍存在明显差异。通过经验发现，最初在 Mamba 中使用的 MVA 模式表现最佳。

Grouped Head Patterns.

多查询注意力的思想可以扩展到分组查询注意力：除了 1 个 K 和 V 头，还可以创建 G 个独立的 K 和 V 头，其中 1 < G 且 G 整除 H。这样做的动机既是为了弥合多查询和多头注意力之间的性能差异，也是为了通过将 G 设置为分片数量的倍数来实现更高效的张量并行。

类似地，Mamba-2 中使用的多输入 SSM 头模式可以轻松扩展到分组输入 SSM (GIS)，或同义地分组值注意力 (GVA)。概括很简单，为了简单起见，省略了细节。

3.6.3 Other SSD Extensions from Linear Attention

将内核特征图的选择视为 Mamba-2 架构中的超参数，并期望其他受注意力机制启发的简单修改也有可能实现。

Kernel Attention Approximations to Softmax Attention.

线性注意力或核注意力的许多变体都是通过将注意力得分 softmax(QK^⊤) 视为由以下部分构成的：

指数核 Z = exp (QK^⊤)，对于某些核特征图，可以通过 Z = ψ(Q)ψ(K)^⊤ 来近似。
通过 M = G/G11^⊤ 对核进行归一化，使得行总和为 1，其中除法按元素进行，并且 1 是全 1 的向量。

在 Mamba-2 中，整合了一个灵活的内核特征图，并将其应用于 B 和 C 分支（对应于注意力中的 K 和 V 分支）。为简单起见和对称性，特征图也可以选择性地应用于 X (V) 分支。这在architecture中由任意非线性表示。默认情况下，仅选择 ψ 作为元素级 Swish / SiLU 函数。

Incorporating a Normalization (Denominator) Term.

为了找到分母项，只需计算 M1。但请记住，模型的最终输出只是 Y = MX。因此，只需在 X 上增加一个额外的列 1，即可找到归一化项，从而得到形状为 (T, P + 1) 的张量。

请注意，在这种情况下，核特征图 ψ 必须为正，这样总和才为正。

3.7 Systems Optimization for SSMs

描述了针对 SSM 的几种系统优化，特别是 Mamba-2 架构，以实现大规模高效训练和推理。具体来说，专注于大规模训练的张量并行和序列并行，以及高效微调和推理的可变长度序列。

3.7.1 Tensor Parallel

张量并行 (TP)是一种模型并行技术，它将每一层（例如注意力、MLP）拆分为多个加速器（例如 GPU）运行。该技术广泛用于在 GPU 集群上训练大多数大型模型，其中每个节点通常有 4-8 个 GPU，并具有 NVLink 等快速网络。TP 最初是为 Transformer 架构开发的，将其改编成其他架构并不简单。首先展示了将 TP 与 Mamba 架构结合使用的挑战，然后展示了 Mamba-2 架构如何设计来提高 TP 效率。

回想一下 Mamba 架构，它具有单个输入 u ∈ ℝ^L × d（为简单起见，没有批处理），输入投影矩阵 W^(x), W^(z) ∈ ℝ^d × ed，其中 e 是扩展因子（通常为 2），输出投影矩阵 W^(o) ∈ ℝ^ed × d：

使用 TP，假设想将计算拆分到 2 个 GPU 上。很容易将输入投影矩阵 W^(x) 和 W^(z) 拆分成两个分区，每个分区的大小为。然后每个 GPU 将保存大小为的 x_c 的一半。但是，由于 Δ, B, C 是 x_c 的函数，因此需要在 GPU 之间进行额外的 all-reduce 以在计算 Δ, B, C 之前获得整个 x_c。之后，这两个 GPU 可以并行计算 SSM，因为它们沿 d 是独立的。最后，可以将输出投影矩阵 W^(o) 拆分成两个分区，每个分区的大小为，并在最后进行 all-reduce。与 Transformers 相比，将使用两次全归约而不是一次，从而使通信时间增加一倍。对于大规模 Transformers 训练，通信可能已经占用了相当一部分时间（例如 10-20%），而通信增加一倍会使 Mamba 在大规模训练中效率降低。

使用 Mamba-2，目标是每个块只有一个全归约，类似于 Transformers 中的注意力或 MLP 块。因此，可以直接从 u 而不是 x_c 获得 Δ, B, C，从而允许拆分这些投影矩阵。这意味着在不同的 GPU 上有不同的 Δ, B, C 集，这相当于在更大的“逻辑 GPU”上有几个 Δ, B, C 的“组”。此外，在每个块内使用 GroupNorm，组数可被 TP 度整除，这样 TP 组中的 GPU 在块内就不会有通信：

只需要拆分输入投影矩阵和输出投影矩阵，并且只需要在块的末尾进行全归约。这类似于 TP 的注意力和 MLP 层的设计。具体来说，如果 TP 度为 2，会将 W^(x) = [W₁^(x), W₂^(x)] 与 W_i^(x) ∈ ℝ^{d × ed/2} 分开，W^(z) = [W₁^(z), W₂^(z)] 与 W_i^(z) ∈ ℝ^{d × ed/2} 分开，并且将与 W_i^(o) ∈ ℝ^{ed/2 × d} 分开。对于 i = 1, 2，TP Mamba-2 层可以写成：

在mamba2_parallelism (左) 中说明了使用 Mamba-2 的张量并行。

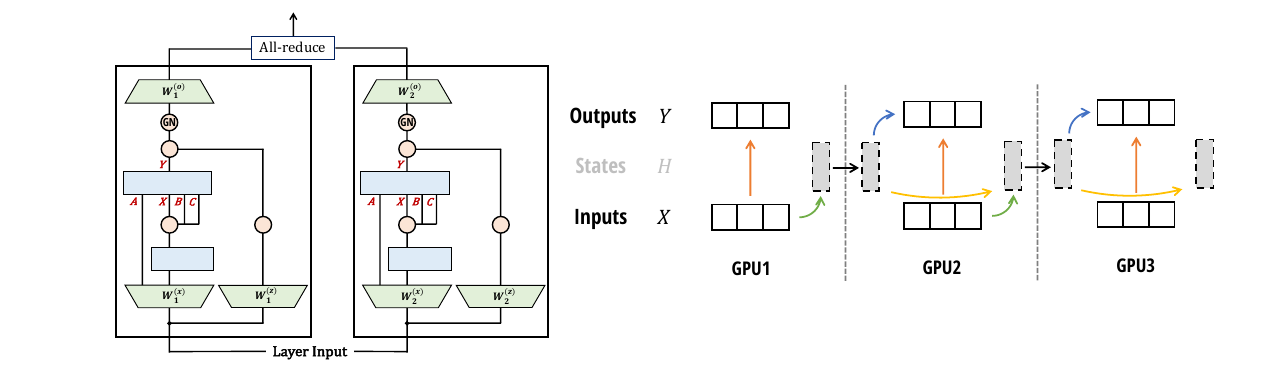
分割输入投影矩阵 W^(x)、W^(z) 和输出投影矩阵 W^(o)。每个 SSM 头 (A, B, C, X) ↦ Y 位于单个设备上。选择 GroupNorm 作为最终规范化层可避免额外的通信。每层需要一个全归约，就像 Transformer 中的 MLP 或注意块一样。(右： 序列/上下文并行)类似于 SSD 算法，使用多个设备，可以沿序列维度进行分割。每个设备计算其序列的状态，然后将该状态传递给下一个 GPU。

3.7.2 Sequence Parallelism

对于非常长的序列，可能需要沿序列长度维度将输入和激活拆分到不同的 GPU。有两种主要技术：

残差和归一化操作的序列并行 (SP)：将 TP 中的 all-reduce 分解为 Reduce-scatter 和 All-gather。注意到残差和归一化操作在同一 TP 组中的所有 GPU 上重复执行相同的输入，SP 通过执行以下操作沿序列长度维度拆分激活：Reduce-scatter、残差和归一化，然后执行 All-gather。

由于 Mamba-2 架构使用相同的残差和归一化结构，因此 SP 无需修改即可应用。

标记混合操作（注意或 SSM）的序列并行，也称为“上下文并行”（CP）。注意力机制中的序列并行的难点在于，可以将查询和键拆分成块，但每个查询块都需要与键块交互，从而导致通信带宽是工作器数量的二次方。

使用 SSM，可以以一种简单的方式拆分序列：每个工作器采用初始状态，根据其输入计算 SSM，返回最终状态，并将该最终状态传递给下一个工作器。通信带宽与工作器数量成线性关系。这种分解与 SSD 算法 (ssd-algorithm) 中拆分成块/块的块分解完全相同。在图mamba2_parallelism (右) 中说明了这种上下文并行。

3.7.3 Variable Length

虽然预训练通常对批次使用相同的序列长度，但在微调或推理期间，模型可能需要处理不同长度的不同输入序列。处理这种情况的一种简单方法是将批次中的所有序列右填充到最大长度，但如果序列长度相差很大，这种方法效率会很低。对于transformer，已经开发出复杂的技术来避免填充并在 GPU 之间进行负载平衡，或者将多个序列打包在同一批次中并调整注意力掩码。特别是使用 SSM 和 Mamba，可以通过将整个批次视为一个长序列来处理可变序列长度，并避免在各个序列之间传递状态。这相当于简单地将一个序列末尾的标记 t 的 A_t = 0 设置为阻止它将信息传递给属于不同序列的标记 t + 1。

3.8 结果

更快的 SSD 算法允许增加状态维度（与 Mamba-1 中的N = 16相比,N = 64或128）。尽管从技术上来说，对于相同的N，Mamba-2 比 Mamba-1 受到更多限制，但较大的状态维度通常会提高模型质量。在这里，展示了在 Pile 上使用 300B 代币训练的模型的结果，其中 Mamba-2 的性能优于 Mamba-1 和 Pythia。

将 Mamba 层与注意力层相结合可以比纯 Transformer 或 Mamba 有所改进。在 2.7B 参数和 300B 令牌规模下验证，仅具有 6 个注意力块（和 58 个 SSD 块）的混合模型优于 64 个 SSD 块以及标准 Transformer++ 基线（32 个门控 MLP 和 32 个注意力块）。

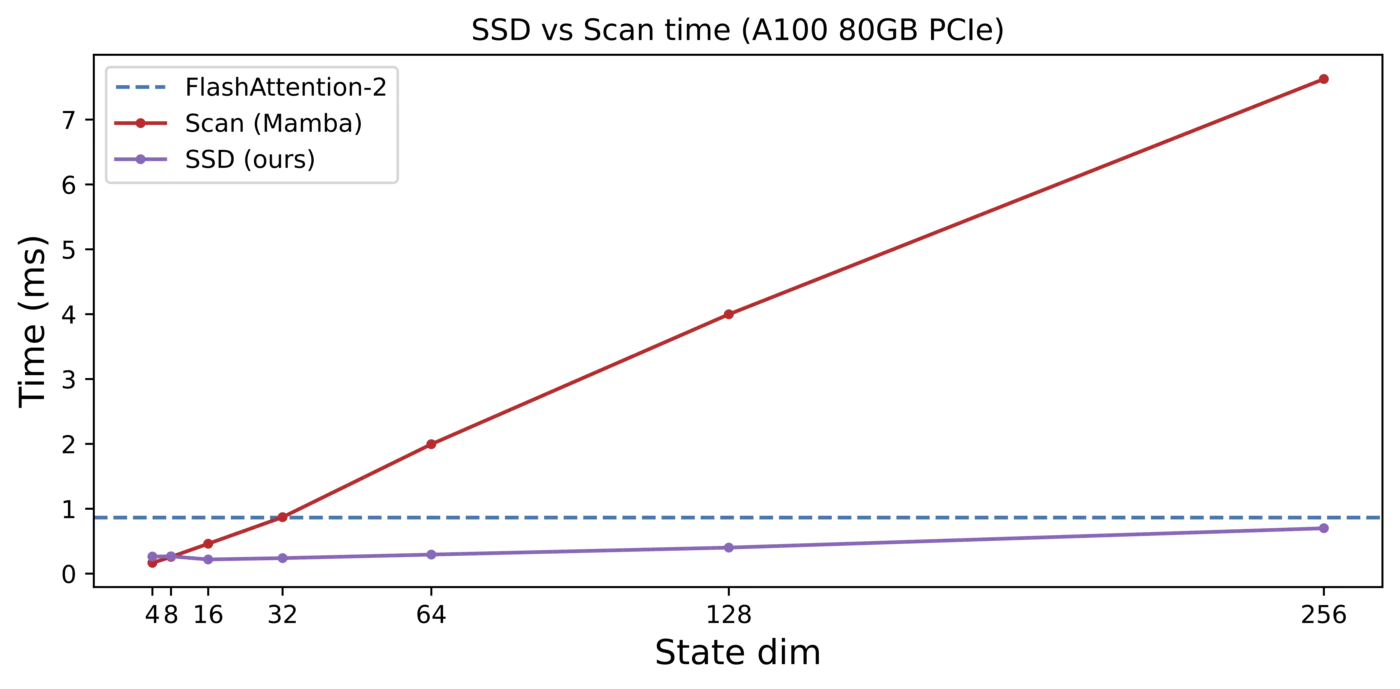
还验证了对于相同的状态维度，SSD 算法比 Mamba-1 的选择性扫描算法要快得多，并且在计算上可以更好地扩展到更大的状态维度。让这些张量核心发挥作用是关键！

参考

LLM

#LLM #Mamba

LLM(十一)——Mamba

https://mztchaoqun.com.cn/posts/D49_Mamba/

作者

mztchaoqun

发布于

2024年11月28日

许可协议

Megatron-LM 上一篇

神经网络(二)——多层感知机（Multilayer Perceptron）下一篇