LLM(五)——Hardware Optimization Attention

一、PagedAttention

vLLM发现LLM 服务的性能受到内存瓶颈的影响。在自回归 decoder 中，所有输入到 LLM 的 token 会产生注意力 key 和 value 的张量，这些张量保存在 GPU 显存中以生成下一个 token。这些缓存 key 和 value 的张量通常被称为 KV cache，其具有以下特点：

• 显存占用大：在 LLaMA-13B 中，缓存单个序列最多需要 1.7GB 显存；
• 动态变化：KV 缓存的大小取决于序列长度，这是高度可变和不可预测的。因此，这对有效管理 KV cache 挑战较大。该研究发现，由于碎片化和过度保留，现有系统浪费了 60% - 80% 的显存。

为了解决这个问题，该研究引入了 PagedAttention，这是一种受操作系统中虚拟内存和分页经典思想启发的注意力算法。与传统的注意力算法不同，PagedAttention 允许在非连续的内存空间中存储连续的 key 和 value 。具体来说，PagedAttention 将每个序列的 KV cache 划分为块，每个块包含固定数量 token 的K和V。在注意力计算期间，PagedAttention 内核可以有效地识别和获取这些块。

将KV块大小表示为B,K块和V块分别表示为：K_j = (k_{(j − 1)B + 1}, …, k_jB)和V_j = (v_{(j − 1)B + 1}, …, v_jB)，则

其中个A_ij = (a_{i, (j − 1)B + 1}, …, a_i, jB)是第j个KV 块上注意力得分的行向量。⌈i/B⌉向上取整，为根据q_i的位置来计算需要累计前多少个K和V块的的向量。

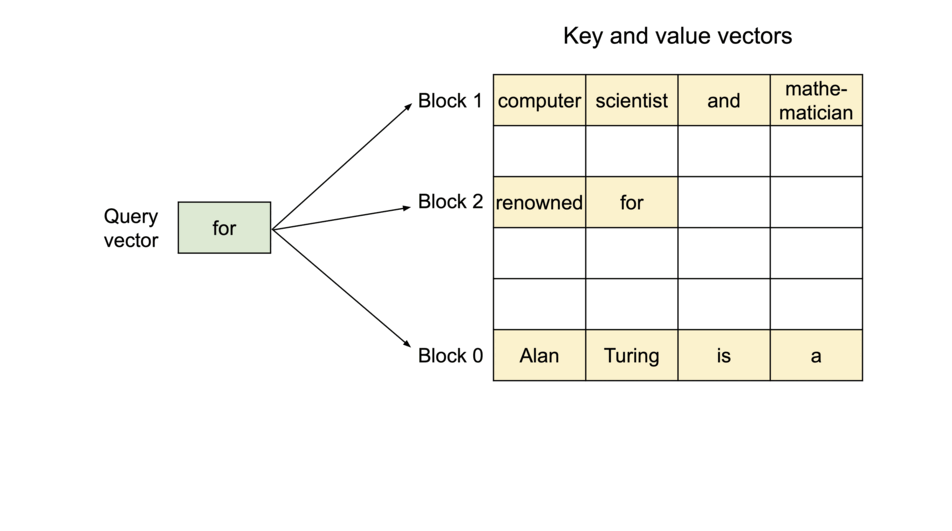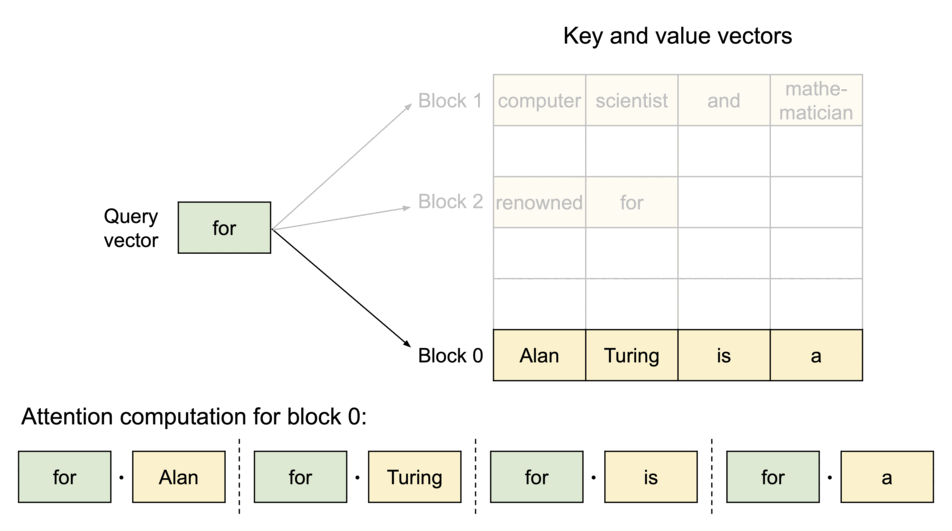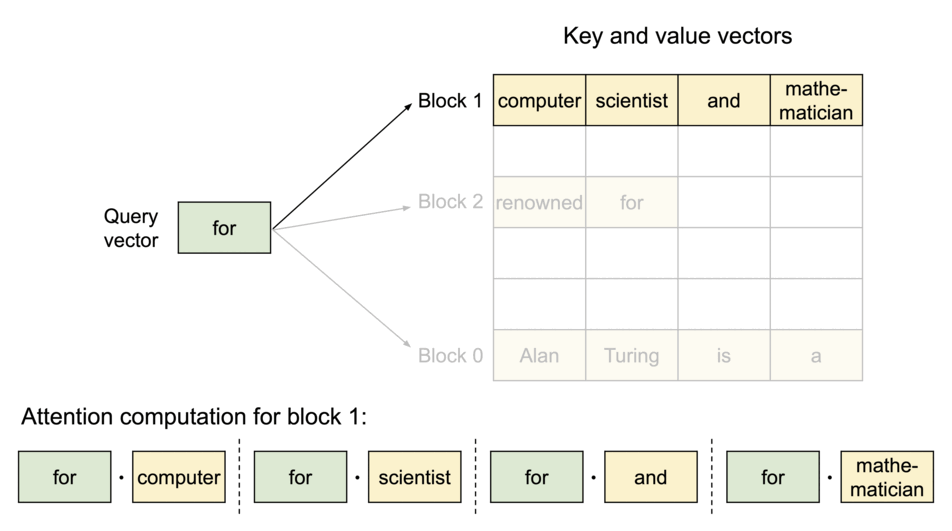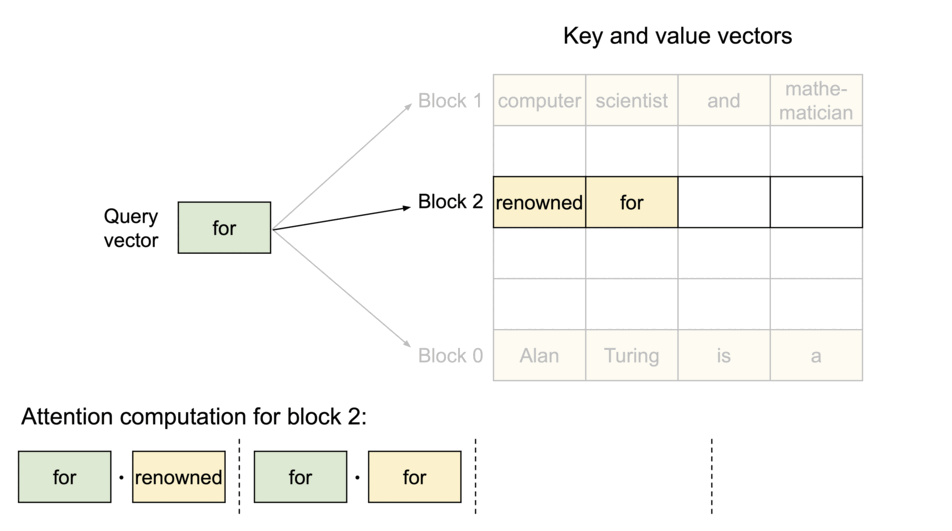
在注意力计算过程中，PagedAttention内核分别识别并获取不同的KV块。上图展示了 PagedAttention 的示例：K和V向量分布在三个块上，并且这三个块在物理内存上并不连续。每次内核都会将查询token(“for”)的查询向量q_i与块中的K向量K_j相乘来计算注意力分数A_ij，然后将A_ij与块中的V向量V_j相乘，得出最终的注意力输出o_i。PagedAttention算法允许KV块存储在非连续的物理内存中，这使得vLLM中的分页内存管理更加灵活。

请求生成过程

因为块在内存中不需要是连续的，所以可以像在操作系统的虚拟内存中一样以更灵活的方式管理键和值：可以将块视为页面，将token视为字节，将序列视为进程。序列的连续逻辑块通过块表映射到非连续物理块。当新token生成时，物理块会按需分配。

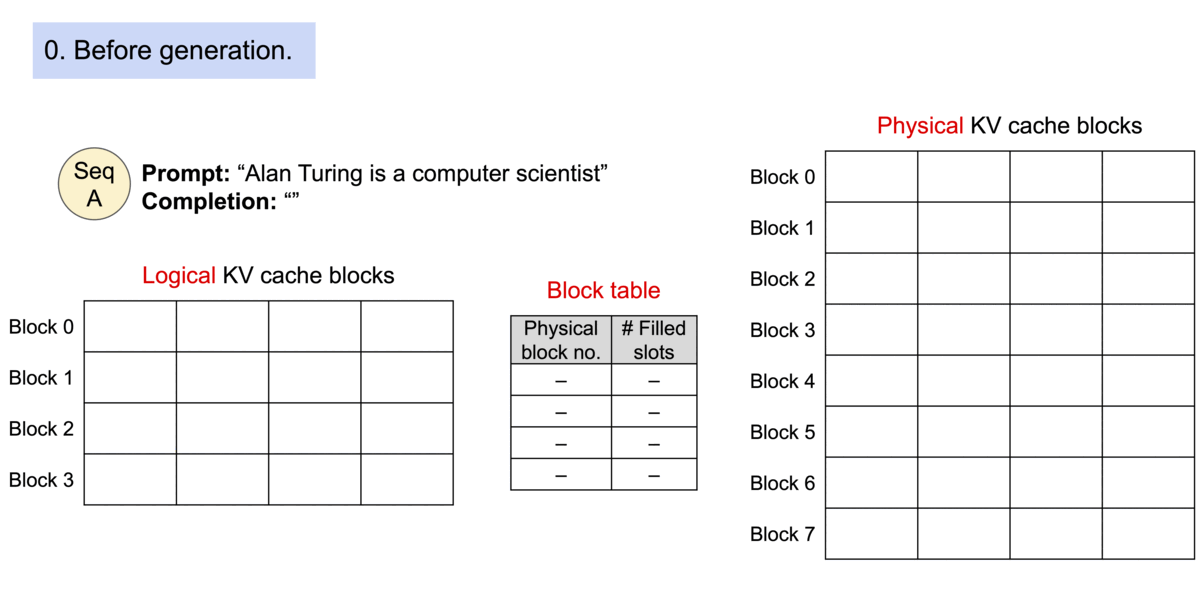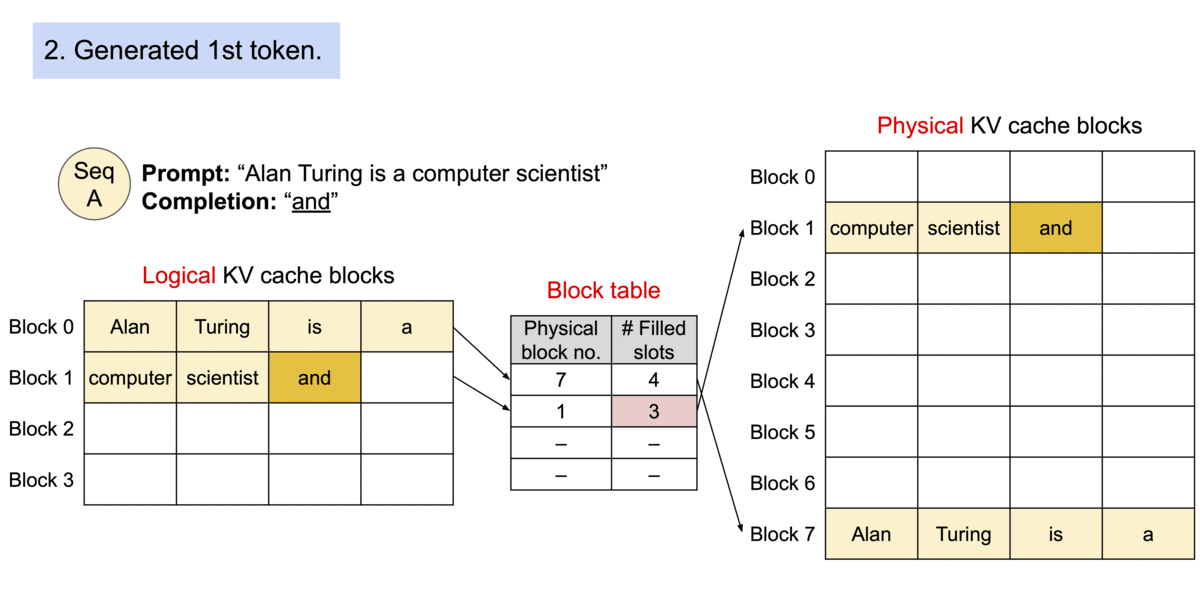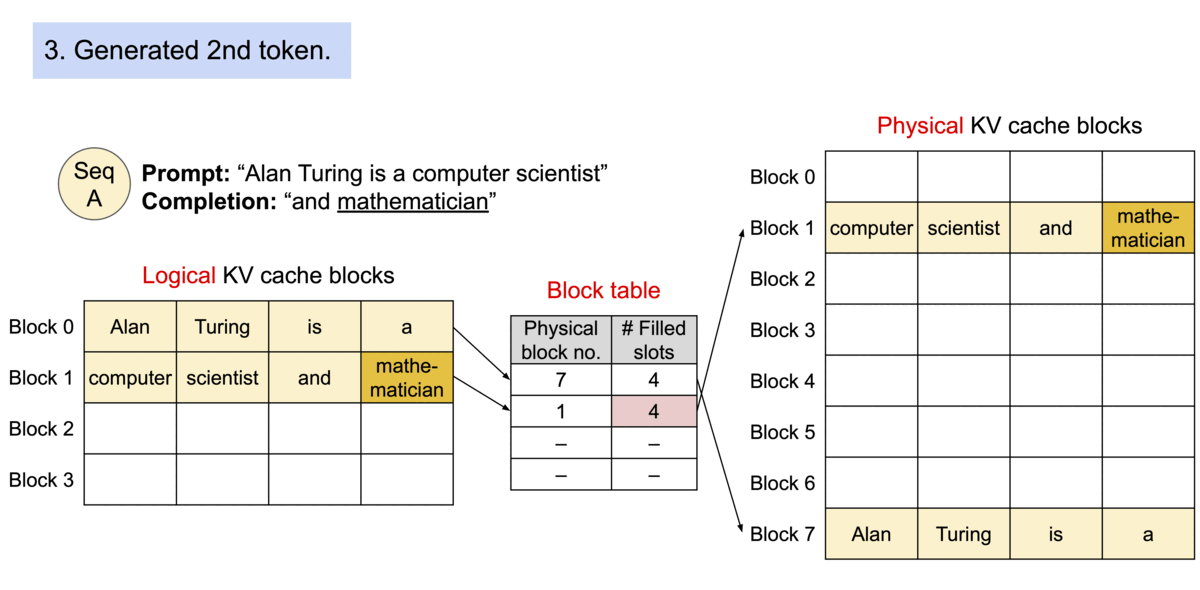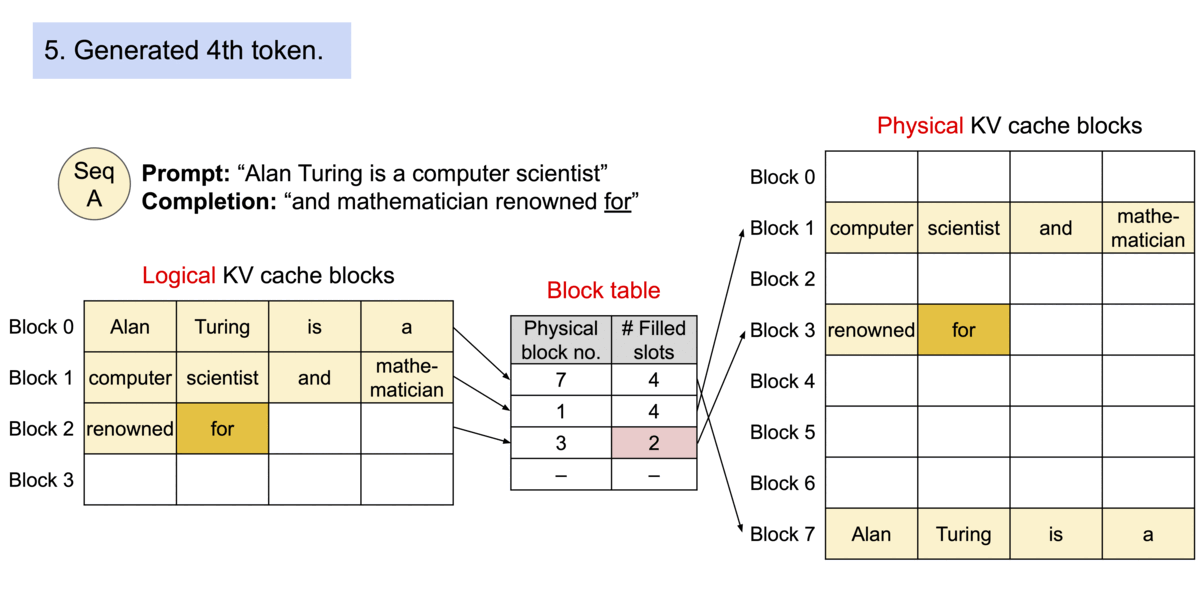
在 PagedAttention 中，内存浪费仅发生在序列的最后一个块中。实际上，这会导致内存使用接近最佳，浪费率低于 4%。事实证明，内存效率的提高非常有益：它允许系统将更多序列一起批处理，提高 GPU 利用率，从而显着提高吞吐量，如上面的性能结果所示。

并行采样示例

PagedAttention 还有另一个关键优势：高效的内存共享。例如，在并行采样中，从同一提示生成多个输出序列。在这种情况下，提示的计算和内存可以在输出序列之间共享。

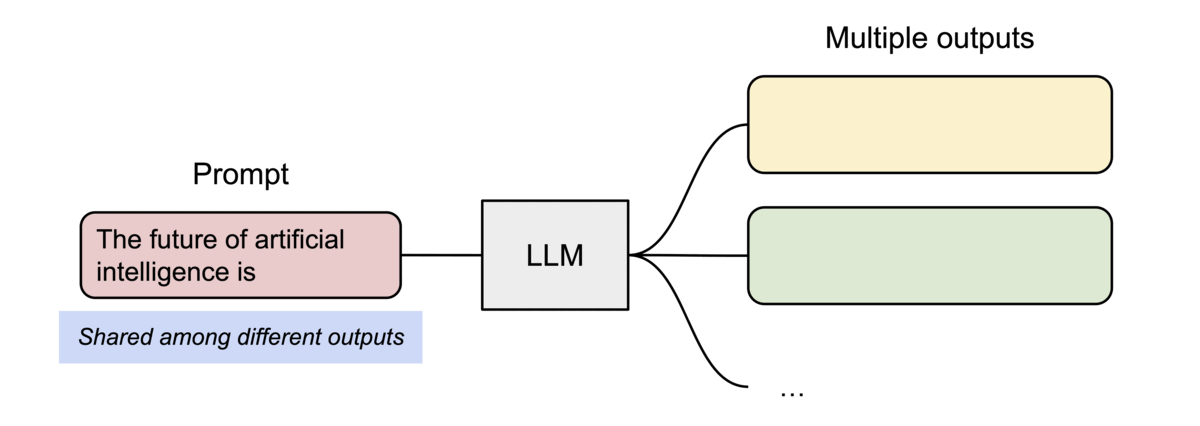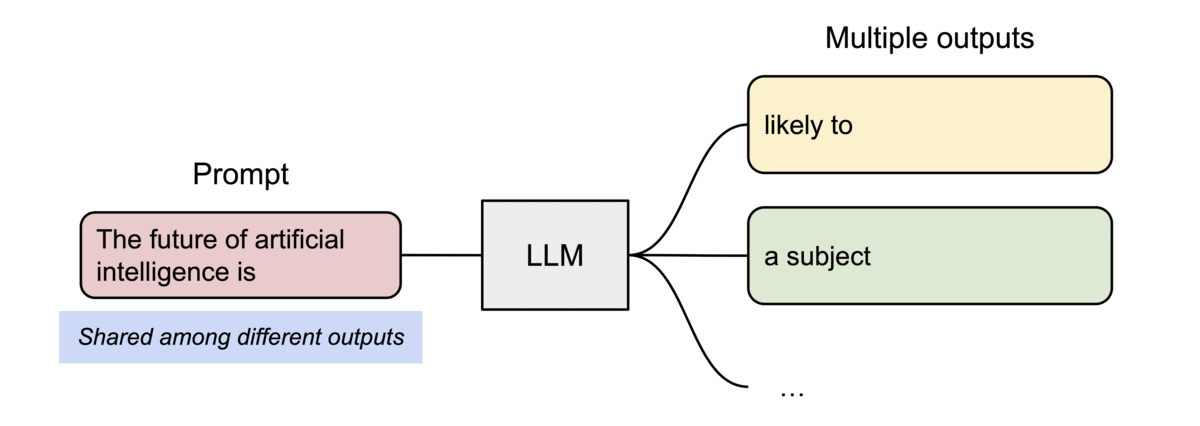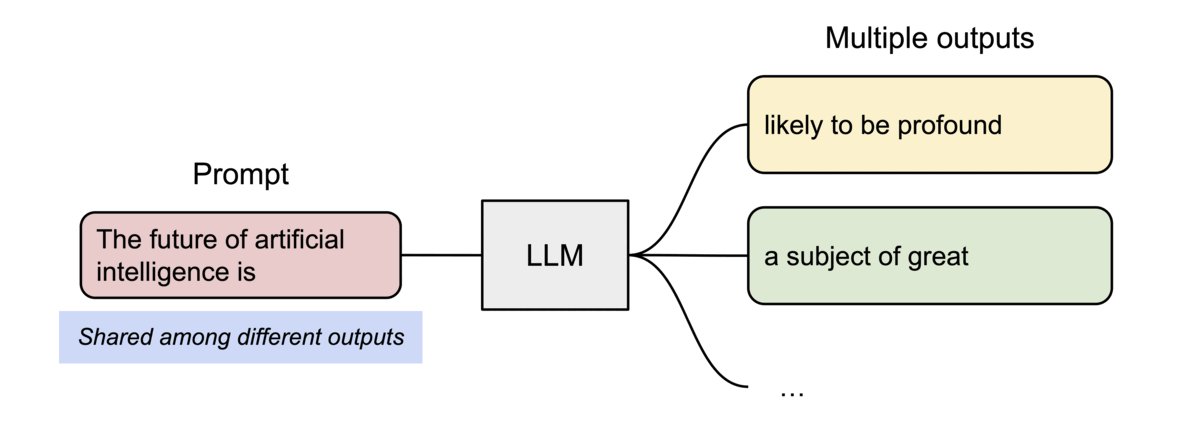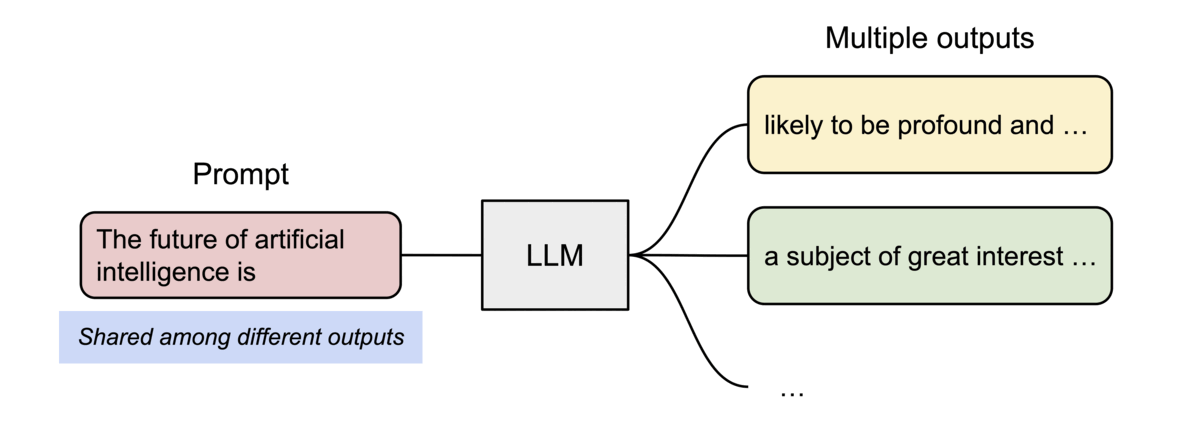
PagedAttention 自然可以通过其块表实现内存共享。与进程共享物理页的方式类似，PagedAttention 中的不同序列可以通过将其逻辑块映射到同一物理块来共享块。为了确保安全共享，PagedAttention 跟踪物理块的引用计数并实现 Copy-on-Write 机制。

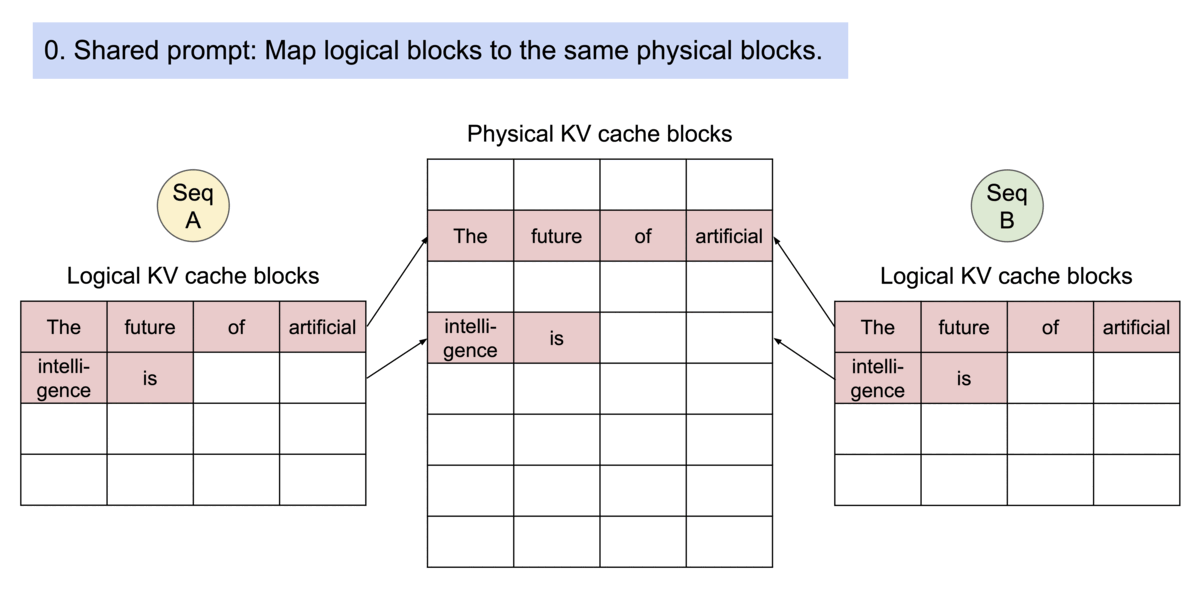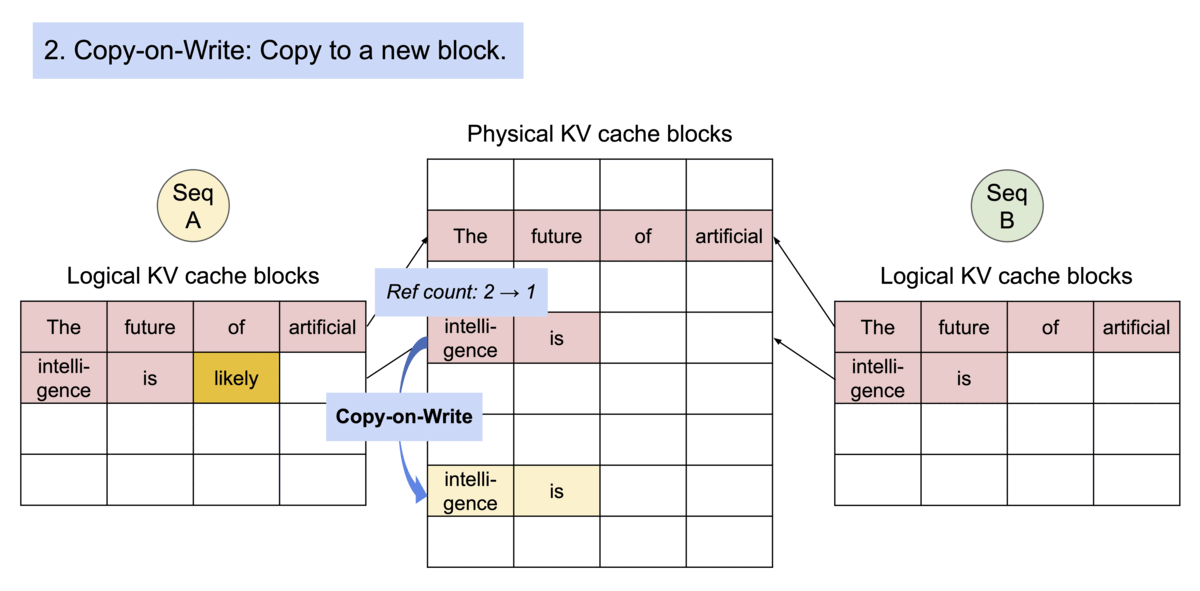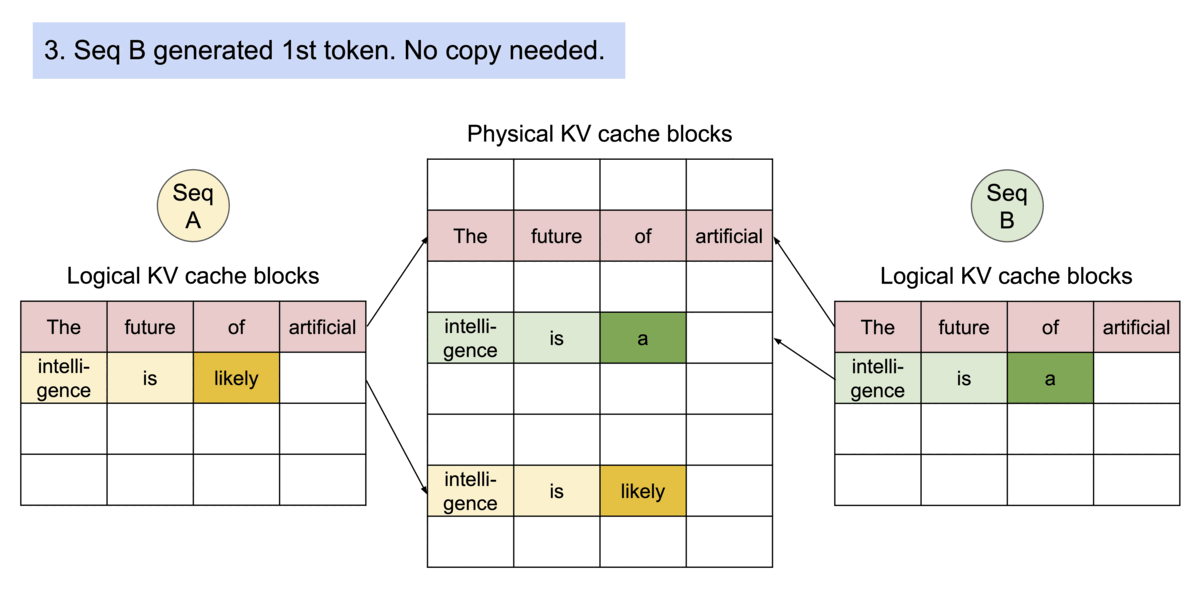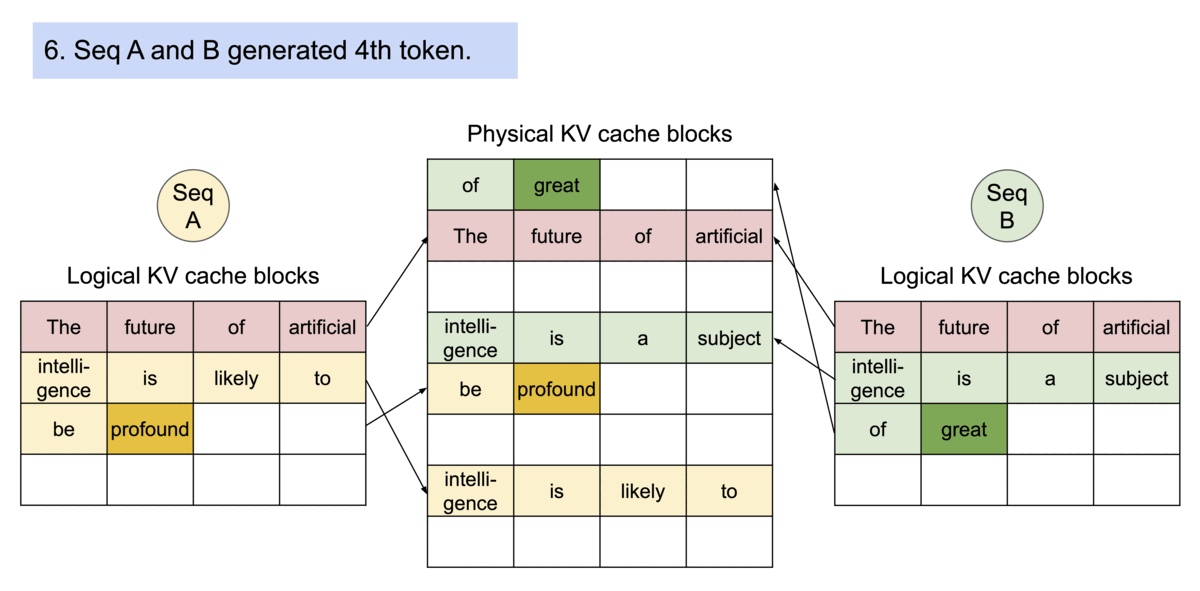
PageAttention 的内存共享极大地降低了复杂采样算法的内存开销，例如并行采样和波束搜索，将其内存使用量减少高达 55%。这可以将吞吐量提高高达 2.2 倍。这使得这种采样方法在LLM服务中变得实用。

官方文档CUDA实现

示例代码

attention计算过程

def ref_masked_attention(
    query: torch.Tensor,
    key: torch.Tensor,
    value: torch.Tensor,
    scale: float,
    attn_mask: Optional[torch.Tensor] = None,
) -> torch.Tensor:
    query = query * scale
    attn = torch.einsum('qhd,khd->hqk', query, key)
    if attn_mask is not None:
        attn = attn + attn_mask
    attn = torch.softmax(attn, dim=-1)
    out = torch.einsum('hqk,khd->qhd', attn, value)
    return out


def ref_single_query_cached_kv_attention(
    output: torch.Tensor,
    query: torch.Tensor,
    key_cache: torch.Tensor,
    value_cache: torch.Tensor,
    block_tables: torch.Tensor,
    context_lens: torch.Tensor,
) -> None:
    num_heads = value_cache.shape[1]
    head_size = value_cache.shape[2]
    block_size = value_cache.shape[3]

    num_input_tokens = query.shape[0]
    for i in range(num_input_tokens):
        q = query[i].unsqueeze(0)
        block_table = block_tables[i]
        context_len = int(context_lens[i])

        keys = []
        values = []
        ## 取出i之前的所有K,V
        for j in range(context_len):
            block_number = int(block_table[j // block_size])
            block_offset = j % block_size

            k = key_cache[block_number, :, :, block_offset, :]
            k = k.reshape(num_heads, head_size)
            keys.append(k)

            v = value_cache[block_number, :, :, block_offset]
            values.append(v)
        keys = torch.stack(keys, dim=0)
        values = torch.stack(values, dim=0)

        scale = 1.0 / (head_size ** 0.5)
        out = ref_masked_attention(q, keys, values, scale)
        out = out.view(num_heads, head_size)
        output[i].copy_(out, non_blocking=True)

完整代码

二、FlashAttention

2.1 背景

传统的注意力算法其内存效率是O(N²)的，尽管已经有许多近似注意力的方法尝试减少attention的计算和内存要求。例如，稀疏近似和低秩近似的方法，将计算复杂度降低到了序列长度的线性或亚线性。但这些近似注意力方法方法并没有得到广泛应用。因为这些方法过于关注FLOPS(浮点数计算次数)的减少，而忽略了IO读写的内存访问开销，导致这并没有效减少运行时间(wall-clock time)。总之，在现代GPU中，计算速度已经远超过了显存访问速度，transformer中的大部分计算操作的瓶颈是显存访问。对于显存受限的操作，IO感知是非常重要的，因为显存读写占用了大部分的运行时间。

GPU的内存由多个不同大小和不同读写速度的内存组成。内存越小，读写速度越快。对于A100-40GB来说，内存分级图如下所示:

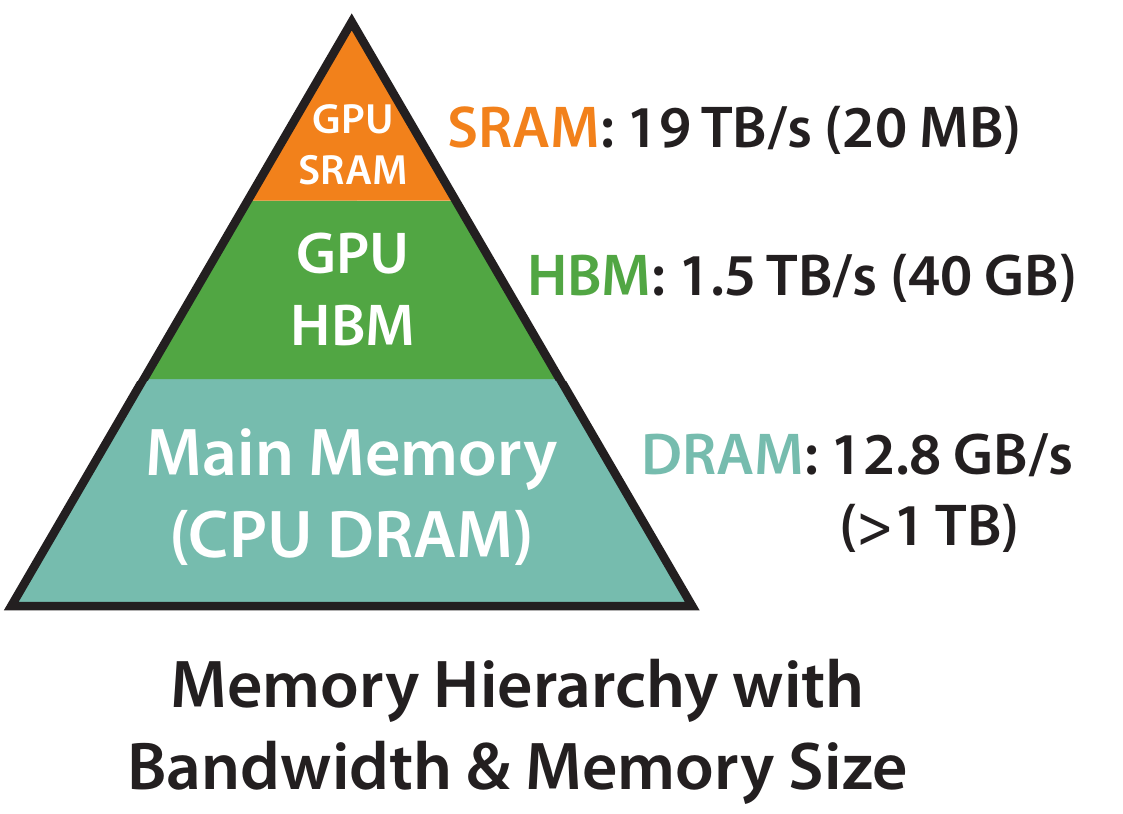
• SRAM内存分布在108个流式多处理器上，每个处理器的大小为192K，合计为192 * 108KB = 20, 736KM = 20MB相当于计算块，但内存小
• 高带宽内存HBM（High Bandwidth Memory），也就是我们常说的显存，大小为40GB。SRAM的读写速度为19TB/s，而HBM的读写速度只有1.5TB/s，不到SRAM的1/10相当于计算慢，但内存大

2.2 标准注意力

标准注意力算法背后的计算逻辑：

标准注意力算法基本上将 HBM 加载/存储操作视为0成本（它并不能感知 IO）。

标准注意力计算公式，如下图

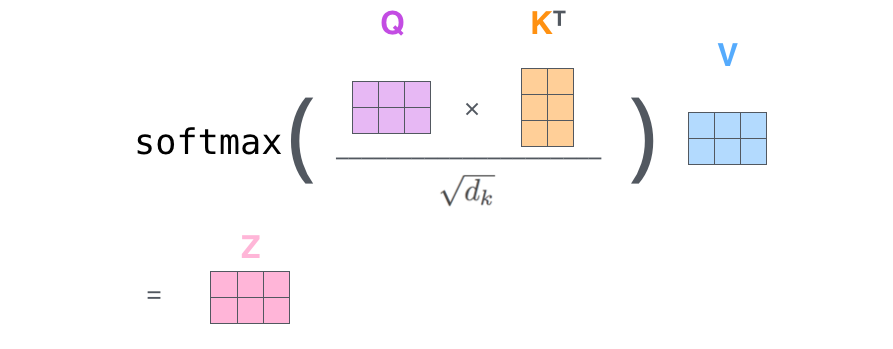
其中Q, K, V ∈ ℝ^N × d，N为序列长度，d为每个注意力头的维度，输出可记为O ∈ ℝ^N × d。上述可以拆分为

如下图

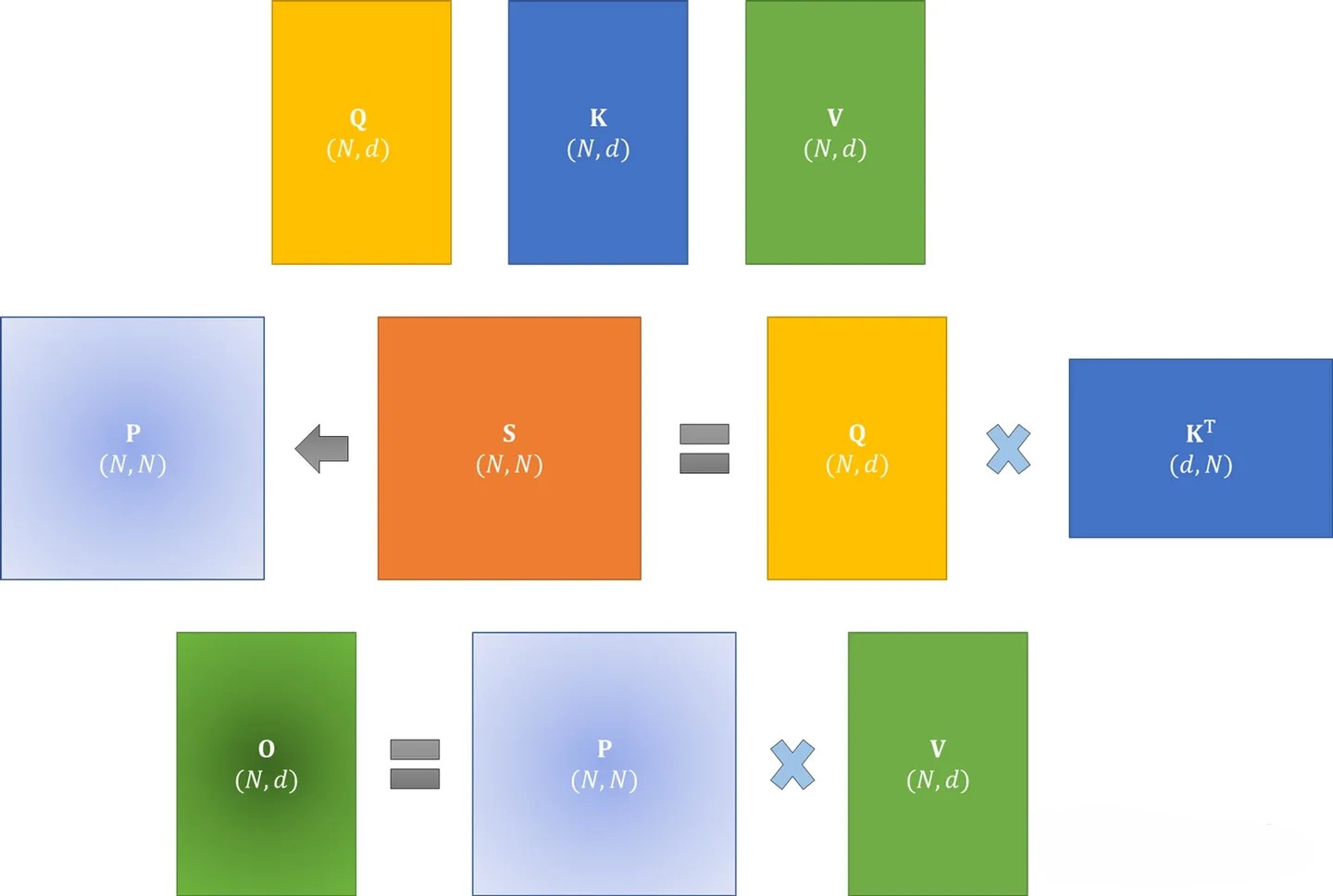
在标准注意力实现中，S, P都要写回到HBM中，占用O(N²)的内存，通常d ≪ N。

标准注意力的过程一共包含八次HBM的矩阵读写操作。这八次读写操作分别为：

• 第一步对Q, K的读共两次，对S的写一次，读写操作总共三次
• 第二步对S读一次，对P写一次，读写操作总共两次
• 第三步对P, V的读共两次，对O的写一次，读写操作总共三次

下图展示了 GPT-2 模型中一个 Attention 算子的完整计算耗时统计：

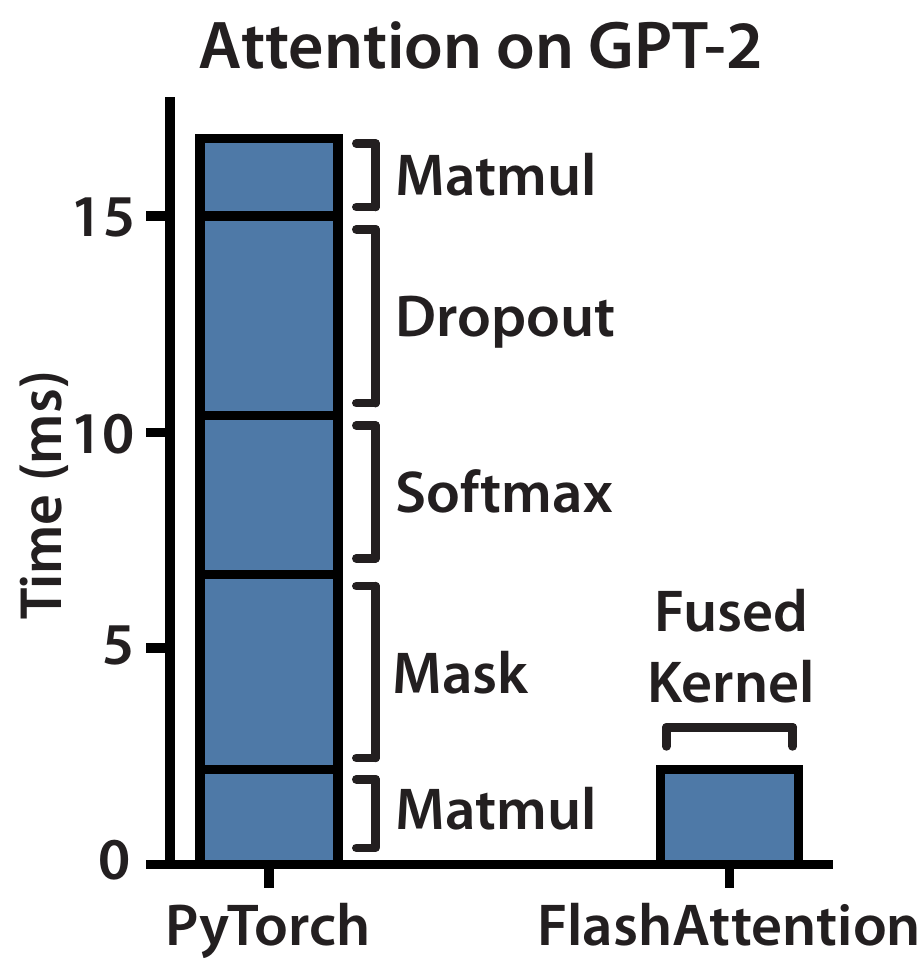
可以看到，masking，softmax 和 dropout 操作占用了大量时间，而主要利用 FLOPS 的矩阵乘法（Matmul）却只占用了一部分时间。HBM读写次数多，减慢了运行时间(wall-clock time)。

2.3 Flash Attention

• GPU有大量的线程来执行某个操作，称为kernel。GPU执行操作的典型方式分为三步：（1）每个kernel将输入数据从低速的HBM中加载到高速的SRAM中；（2）在SRAM中，进行计算；（3）计算完毕后，将计算结果从SRAM中写入到HBM中。
• 对于性能受限于内存带宽的操作，进行加速的常用方式就是kernel融合。kernel融合的基本思想是：避免反复执行“从HBM中读取输入数据，执行计算，将计算结果写入到HBM中”，将多个操作融合成一个操作，减少读写HBM的次数。

FlashAttention 思路是：既然标准注意力算法要将 S 写回 HBM，而这个步骤只为了重新加载计算 Softmax，那么我们可以将其保存在 SRAM 中，等执行完所有中间步骤后，再将最终结果写回 HBM。如下图所示：

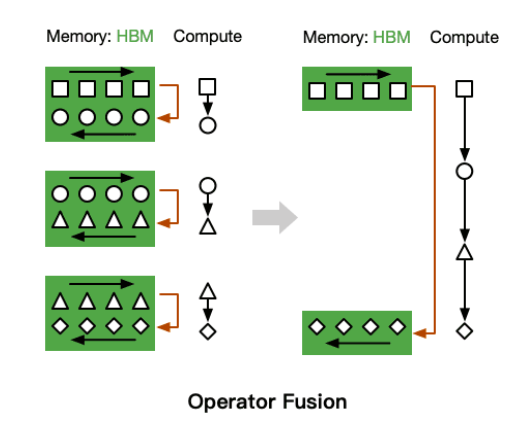
可以看到 FlashAttention 将多个操作融合在一起，其只从 HBM 加载一次，执行融合的算子操作，然后将结果写回 HBM。融合操作主要采用了如下两种技术：

• Tiling：矩阵分块计算，在不访问整个输入的情况下计算 Softmax 函数的缩减，在前向和后向传播时都使用；

• Recomputation：时间换空间，不存储中间注意力矩阵而采用重计算的方式，仅在后向传播时使用。

2.3.1 Tiling

虽然通过kernel融合的方式，将多个操作融合为一个操作，利用高速的SRAM进行计算，可以减少读写HBM的次数，从而有效减少内存受限操作的运行时间。但有个问题是:

SRAM的内存大小有限，不可能一次性计算完整的注意力，因此必须进行分块计算，使得分块计算需要的内存不超过SRAM的大小相当于，内存受限 –> 减少HBM读写次数 –> kernel融合 –> 满足SRAM的内存大小 –> 分块计算，因此分块大小block_size不能太大，否则会导致OOM。

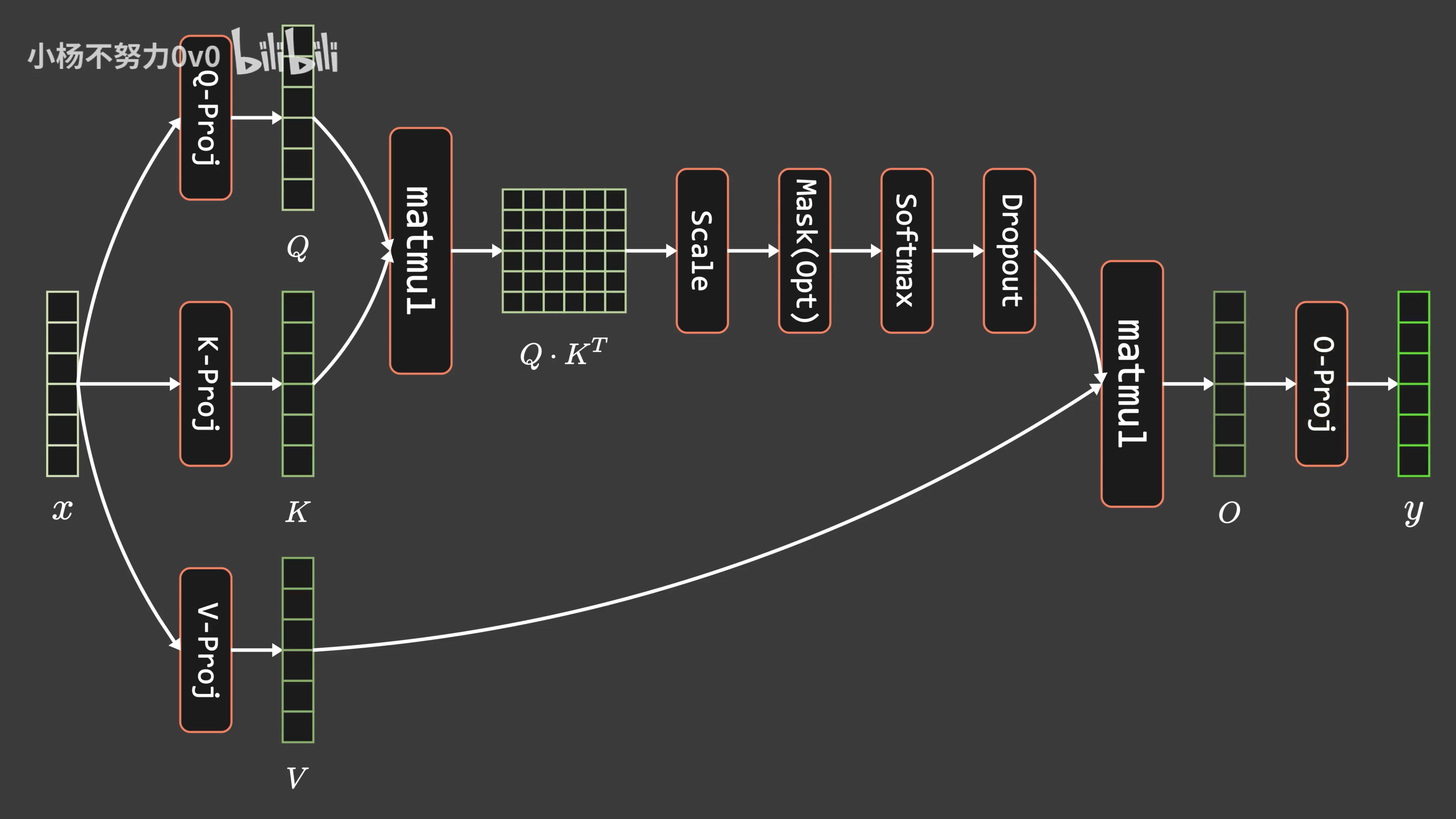
总之，tiling分块计算可以用一个CUDA kernel来执行注意力的所有操作。从HBM中加载输入数据，在SRAM中执行所有的计算操作(矩阵乘法、mask、softmax、dropout、矩阵乘法)，再将计算结果写回到HBM中。

分块计算的难点是什么呢？注意力机制的计算过程是“矩阵乘法 –> scale –> mask –> softmax –> dropout –> 矩阵乘法”，矩阵乘法和逐点操作（scale，mask，dropout）的分块计算是容易实现的，难点在于softmax的分块计算。由于计算softmax的归一化因子（分母）时，需要获取到完整的输入数据，进行分块计算的难度比较大。

tiling的主要思想是分块计算注意力。分块计算的难点在于softmax的分块计算,softmax与K的列是耦合的, 通过引入了两个额外的统计量m(x)和l(x)来进行解耦, 实现了分块计算。为了保证数值稳定性, 对于 x ∈ ℝ^B，执行“减去最大值”的safe softmax的计算过程如下:

对于两个向量x⁽¹⁾, x⁽²⁾ ∈ ℝ^B, 解耦拼接向量的softmax计算: 通过保持两个额外的统计量 m(x), ℓ(x)，可以实现softmax的分块计算。需要注意的是, 可以利用GPU多线程同时并行计算多个block的softmax。为了充分利用硬件性能, 多个block的计算不是串行 (sequential) 的, 而是并行的。

通过例子说明如何分块计算softmax。对向量 [1, 2, 3, 4]计算softmax, 分成两块[1, 2]和[3, 4]进行计算。计算block 1:

计算block2:

合并得到完整的softmax结果：

总的来说，Flash Attention通过调整注意力的计算顺序，引入两个额外的统计量进行分块计算，避免了实例化完整的N × N的注意力矩阵S, P，将显存复杂度从O(N²)降低到了O(N)。Flash Attention还通过kernel融合和分块计算，大量减少了HBM访问次数，尽管由于后向传递中的重计算增加了额外的计算量FLOPs，但总的来讲，最终还是减少了不少的运行时间，计算速度更快。

2.3.2 Flash Attention算法的前向计算算法

在忽略mask和dropout的情况下，简化分析，Flash Attention算法的前向计算过程如下所示:

首先，Q, K, V ∈ ℝ^N × d要在HBM中，SRAM的大小为M。N是序列长度，d是每个注意力头的维度

1. 设置块大小

   • 是因为Q、K和V向量是d维的，所以还需要将它们组合成输出的d维向量。所以这个大小基本上允许用Q,K,V和0个向量最大化SRAM的容量,以GPT2和A100为例

   • A100的SRAM大小为M = 192KB = 196608B

   • GPT2中N = 1024, d = 64,对应的Q, K, V的维度为N × d = 1024 × 64,中间结果S, P的维度大小N × N = 1024 × 1024,

   • 所以B_c = ⌈196608/4/64⌉ = 768;  B_r = min (768, 64) = 64

2. 在 HBM 中初始化 O = (0)_N × d ∈ ℝ^N × d, ℓ = (0)_N ∈ ℝ^N, m = (−∞)_N ∈ ℝ^N

   • 用全0初始化输出矩阵O，它将作为一个累加器
   • ℓ类似上文的ℓ(x)其目的是保存softmax的累积分母——exp分数的总和
   • m类似上文的m(x)，其逐行保存最大分数，且初始化为-inf，因为将对其进行Max运算符，因此无论第一个块的Max是什么，它肯定大于-inf

3. 将 Q 分成 个块 Q₁, …, Q_Tr，每个块大小为 B_r × d；将 K, V 分成 个块 K₁, …, K_Tc 和 V₁, …, V_Tc，每个块大小为 B_c × d

   • 按照步骤1中的块大小，将Q, K, V分成块具体来说，则是Q沿着行方向分为T_r块，每一分块的大小为B_r × d
   • K, V沿着行方向分为T_c块，每一分块的大小为B_c × d而T_c = ⌈1024/768⌉ = 2; T_r = ⌈1024/64⌉ = 16

4. 将 O 分成 T_r 个块 O_i, …, O_Tr，每个块大小为 B_r × d；将 ℓ 分成 T_r 个块 ℓ_i, …, ℓ_Tr，每个块大小为 B_r；将 m 分成 T_r 个块 m₁, …, m_Tr，每个块大小为 B_r

   • 将O, l, m分割成块，其中，O, Q的块大小相同，也是沿着行方向分为T_r块，每一分块的大小为B_r × d
   • 至于向量l和向量m则分为T_r块，每一块子向量大小为B_r

综合上述3、4两个步骤：先后切分Q, K, V, O, l, m，可以得到各个分块之间的关系如下:

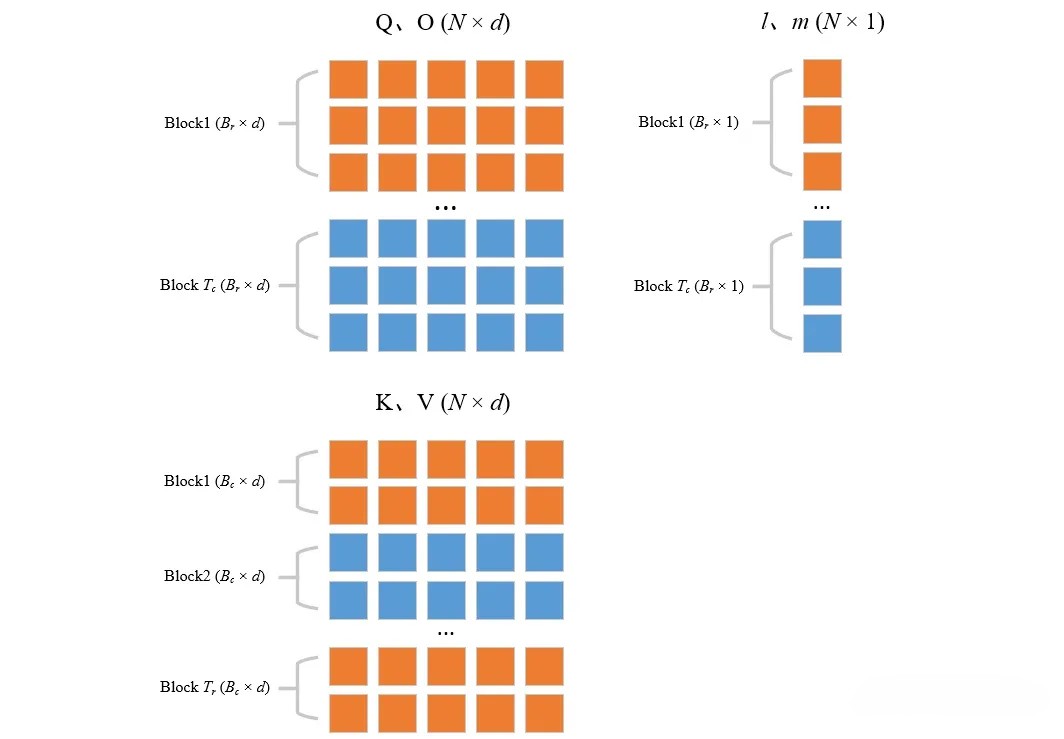
切分完之后，接下来开启两大循环，先外(列)循环 再内(行)循环

5. for 1 ≤ j ≤ T_c

   • 开始跨列循环(即外部循环，由T_c控制，从上一列到下一列)，即跨K/V向量，即遍历K, V，一共循环T_c = 2次。

如果不考虑缩放、softmax等因素，q4k2 v2，便对应图中虚线框里的那个块

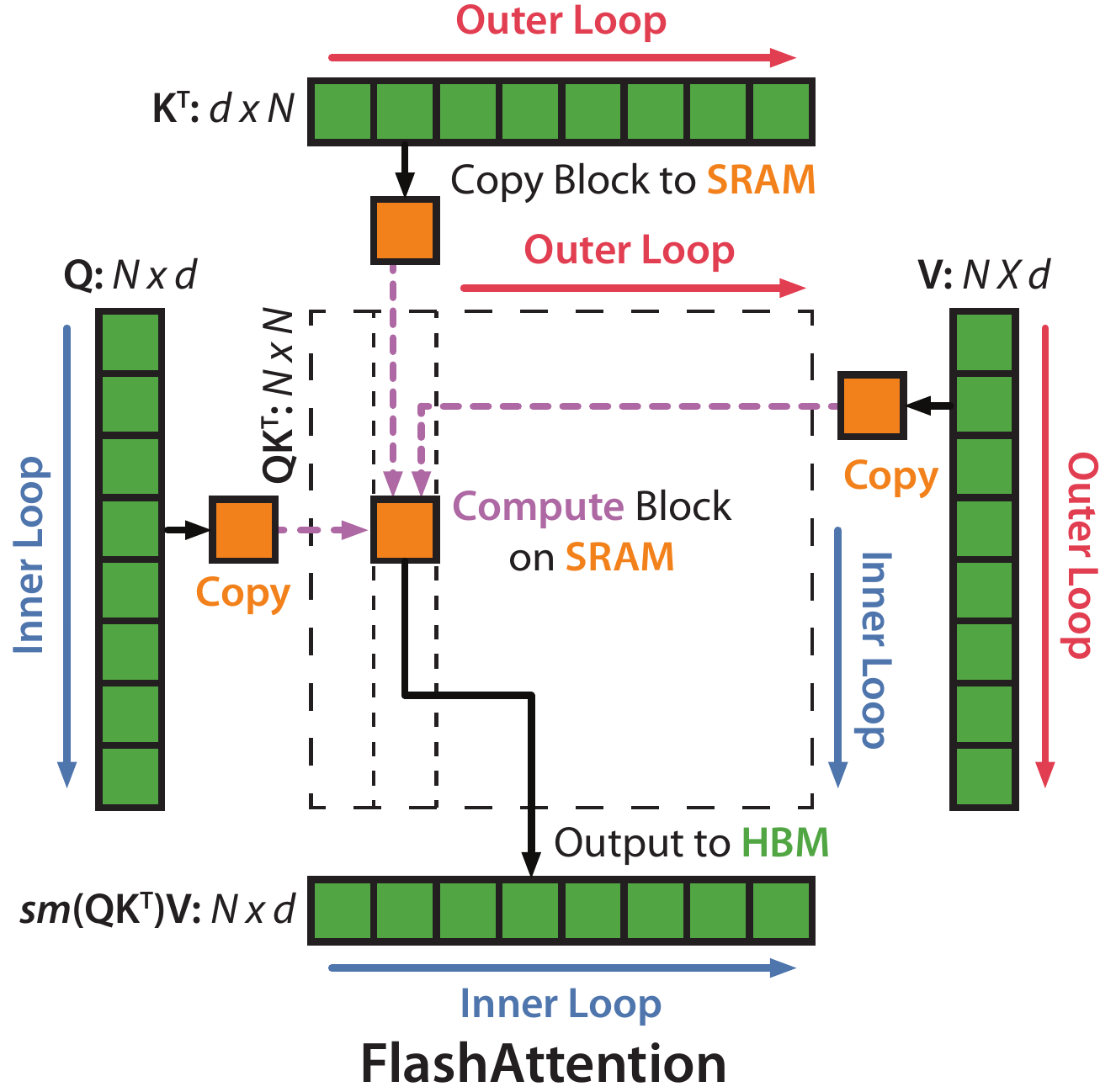
6.    将 K_j, V_j 从慢速HBM 加载到片上快速SRAM

   • 将K_j和V_j块从HBM加载到SRAM(它们的大小为B_c × d = 768 × d)
   • 在这个时间点上仍然有50%的SRAM未被占用(专用于Q和O)

7.    for 1 ≤ i ≤ T_r

   • 开始跨行内部循环(从上一行到下一行)，即跨查询向量，一共循环T_r = 16次，可只在遍历Q, O, l, m

8.     将 Q_i, O_i, ℓ_i, m_i 从 HBM 加载到片上 SRAM

   • 将Q_i(B_r × d = 64 × d)和O_i(B_r × d = 64 × d)块以及l_i(B_r)和m_i(B_r)加载到SRAM中
   • 这里需要保证l_i和m_i能够载入SRAM(包括所有中间变量)

9.     在芯片上，计算 S_ij = Q_iK_j^T ∈ ℝ^{B_r × B_c}

   • 这一步计算Q_i(B_r × d)和K_j转置(d × B_c)之间的点积，得到分块的Attention Score S_ij = Q_iK_i^T ∈ ℝ^{B_r × B_c}

   • 在标准的Transformer计算中Attention Score是一个 N × N的矩阵，如下图所示(图中N = 12,B_r = 3,B_c = 2)

     当j = 0，遍历i 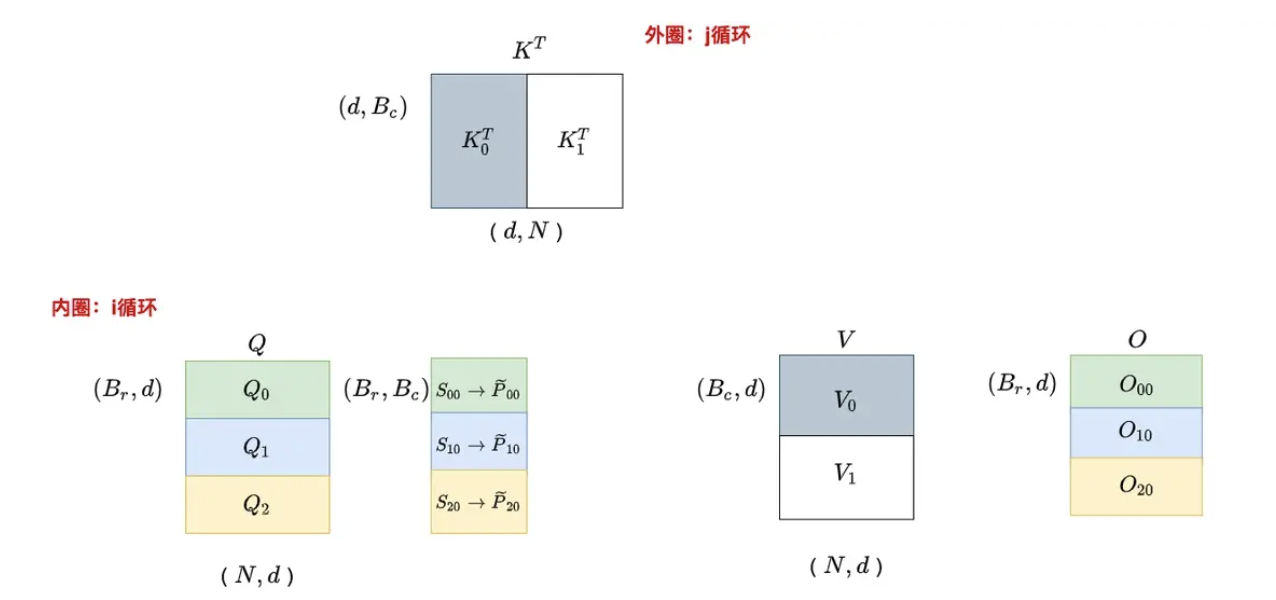当j = 1，遍历i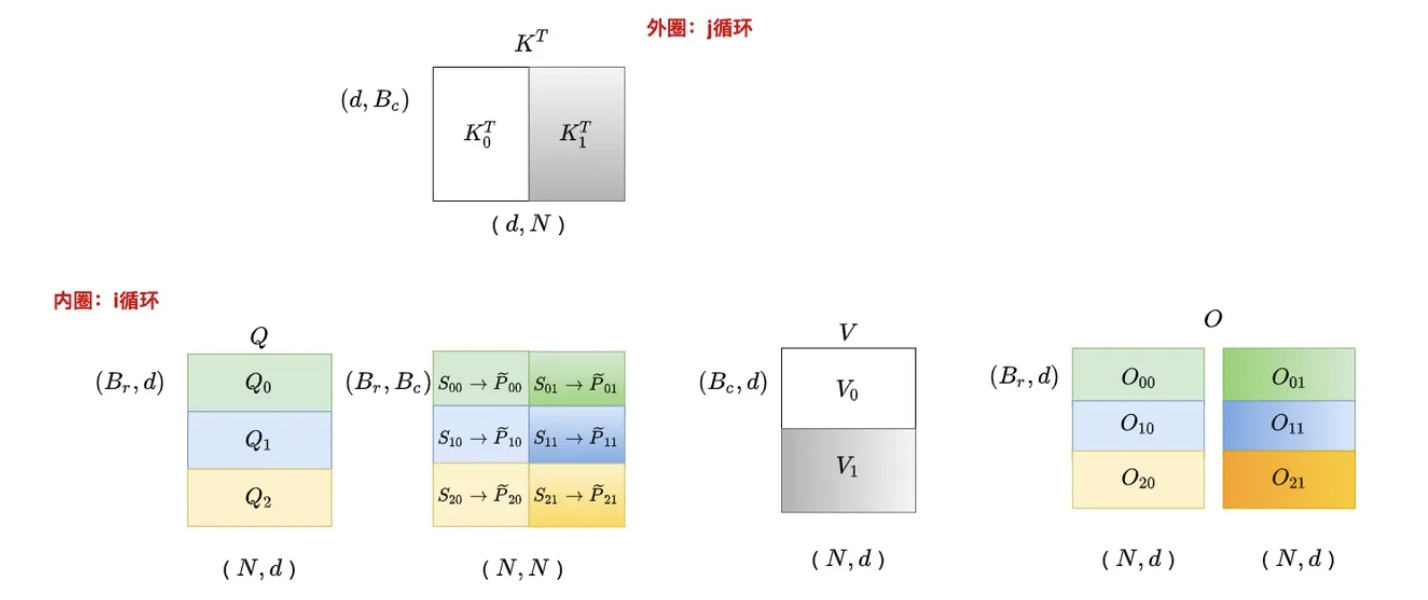

10.     在芯片上，计算m̃_ij = rowmax(S_ij) ∈ ℝ^B_r、（逐点）、

    • 使用上一步计算的分数计算m̃_ij、ℓ̃_ij和
    • 对分块的Attention Score S_ij，计算它每一行中的最大值m_ij = rowmax(S_ij) ∈ ℝ^B_r
    • 基于m̂_ij，计算指数项(归一化-取行最大值并从行分数中减去它，然后EXP)：P̂_ij = exp(S_ij − m̂_ij) ∈ ℝ^{B_r × B_c}
    • 然后再基于P̂_ij，计算EXP求和项(矩阵P的逐行和)：l̂_ij = rowsum(P̂_ij) ∈ ℝ^B_r

11.     在芯片上，计算 m_i^new = max (m_i, m̃_ij) ∈ ℝ^B_r，ℓ_i^new = e^{m_i − m_inew}ℓ_i + e^{m̃_ij − m_inew}ℓ̃_ij ∈ ℝ^B_r

    • 这一步是计算m_i^new 和ℓ_i^new ，举个例子，如下图所说：

    

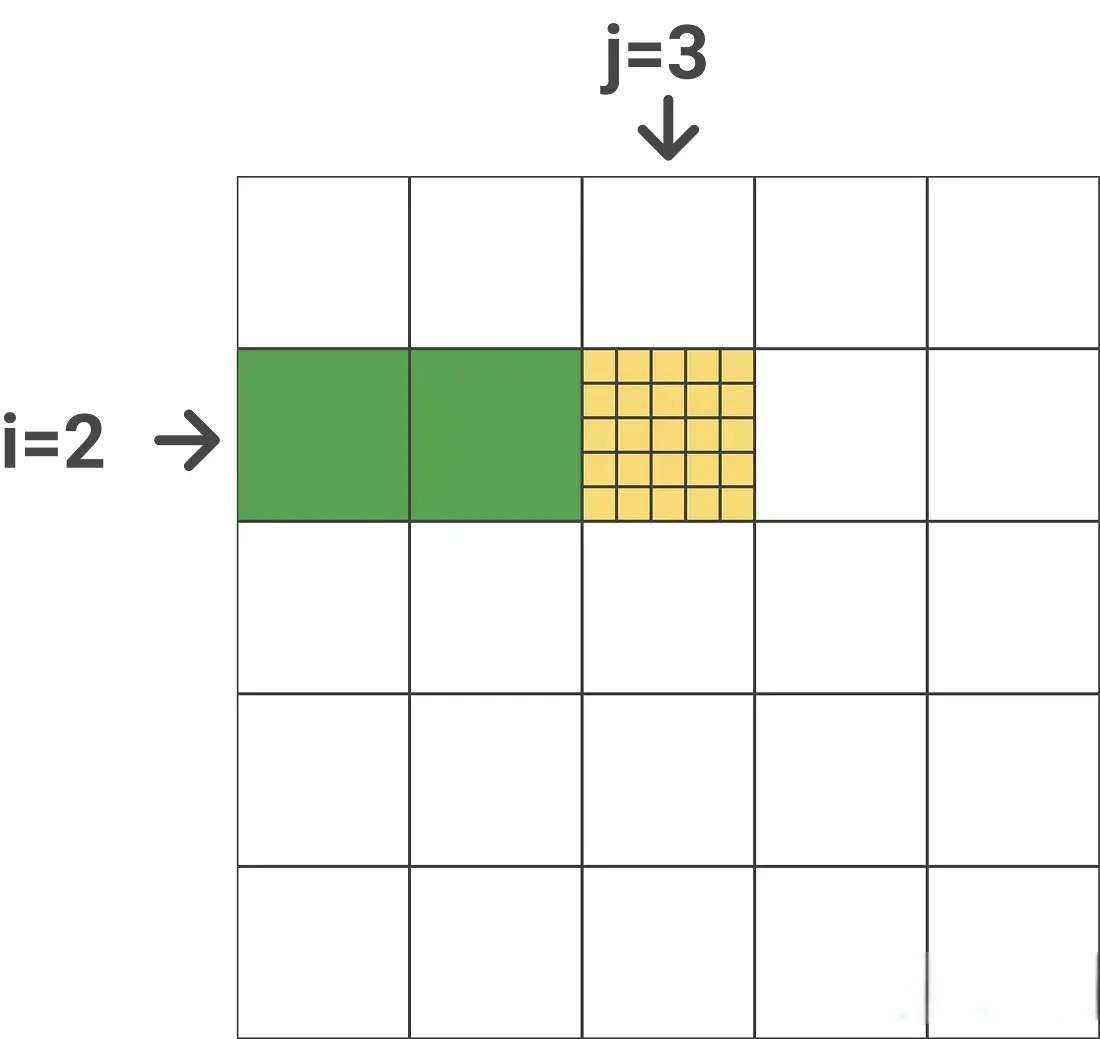
    • m_{i}包含之前所有块的逐行最大值(j = 1&j = 2，用绿色表示)，m̃_ij包含当前块的逐行最大值(用黄色表示)。
    • 为了得到m_i^new 只需要在m̃_ij和m_i之间取一个最大值，ℓ_i^new 也类似

12.     将 写入 HBM

    • 在第9步中，每一个小分块 S_ij有多行(图中为3行)，但行与行之间的数据不会有任何的交互，只是一种Batch计算的策略。真正的分块意义是在列上，因为softmax是沿着列方向进行的
    • 所以为了方便理解，可以想象为 B_r 等于1，即每一次只计算上上图中的一个大小为 (1 × B_c)的分块
    • 基于上述的简化方法，接下来看整个softmax的更新过程。首先，用 S_i 来表示每一行的Attention Score，用 SM_i 表示每一行的softmax

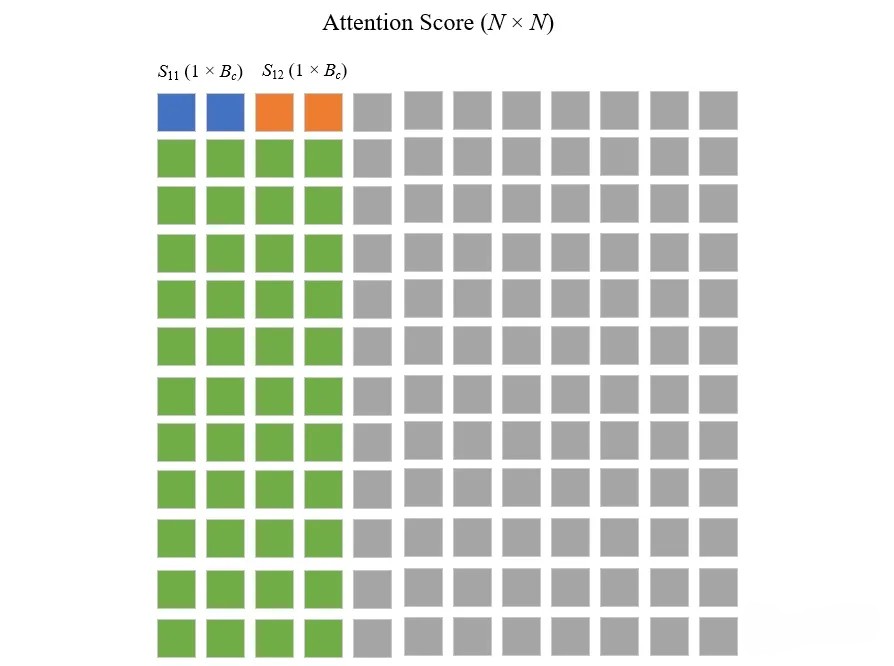
13.     将 ℓ_i ← ℓ_i^new, m_i ← m_i^new 写入 HBM

    • 更新l_i和m_i

14.   end for

15. end for

16. Return O.

2.4 kernel融合中的mask和dropout

给定输入Q, K, V ∈ R^N × d，计算得到注意力输出O^N × d

其中， τ是softmax的缩放因子，典型的比如 。MASK操作将输入中的某些元素置为−inf ，计算softmax后就变成了0，其他元素保持不变

• causal-lm结构和prefix-lm结构的主要差别就是MASK矩阵不同
• dropout (x, p)逐点作用在x的每个元素上，以 p 的概率将该元素置为0，以 1 − p 的概率将元素置为

三、FlashAttention-2

Flash Attention仍然不如其他基本操作(比如矩阵乘法)高效:

• 虽然Flash Attention已经比标准的注意力实现快2-4倍，但前向传播仅达到设备理论最大FLOPs/s的30-50%，而反向传播更具挑战性，仅达到A100 GPU最大吞吐量的25-35%
• 相比之下，优化的矩阵乘法可以达到理论最大设备吞吐量的80-90%。 通过仔细的分析，观察到Flash Attention在GPU上不同线程块和线程束之间的工作划分仍然不够优化，导致低占用率或不必要的共享内存读写

FlashAttention2是在FlashAttention基础上提出的，具有更好的并行性和工作分区

1. 调整算法以减少非矩阵乘法操作的浮点运算次数，同时保持输出不变。
   • 尽管非矩阵乘法操作仅占总浮点运算次数FLOPs的一小部分，但执行非矩阵乘法操作的时间较长。原因在于GPU具有专门用于矩阵乘法的计算单元，Nvidia GPU上的张量核心，可让矩阵乘法的吞吐量相比非矩阵乘法高达16倍。以A100 GPU为例，其FP16/BF16矩阵乘法的最大理论吞吐量为312 TFLOPs/s，而非矩阵乘法的FP32吞吐量仅为19.5 TFLOPs/s。换言之，每个非矩阵乘法的FLOP比矩阵乘法的FLOP贵16倍。因此，减少非矩阵乘法操作的浮点运算次数并尽可能多地执行矩阵乘法操作非常重要。
2. 在序列长度维度上同时并行化前向传播和反向传播，除了批次和头数维度。 这样做可以提高GPU资源的利用率，特别是在序列较长(因此批次大小通常较小)的情况下。
3. 即使在注意力计算的一个块内部，也将工作分配给不同的线程块以减少通信和共享内存的读写

3.1 Flash Attention V2 前向传播层面的改进

3.1.1 Flash Attention 前向传播算法

1. 为简单起见，仅考虑注意矩阵 S 的一个行块，其形式为，其中矩阵 S⁽¹⁾, S⁽²⁾ ∈ ℝ^{B_r × B_c}，B_r 和 B_c 分别是行块和列块大小。
2. 要计算此行块的 softmax，并将其与以下值相乘，形式为 ，其中矩阵 V⁽¹⁾, V⁽²⁾ ∈ ℝ^B_c × d。
3. 标准 softmax 将计算：

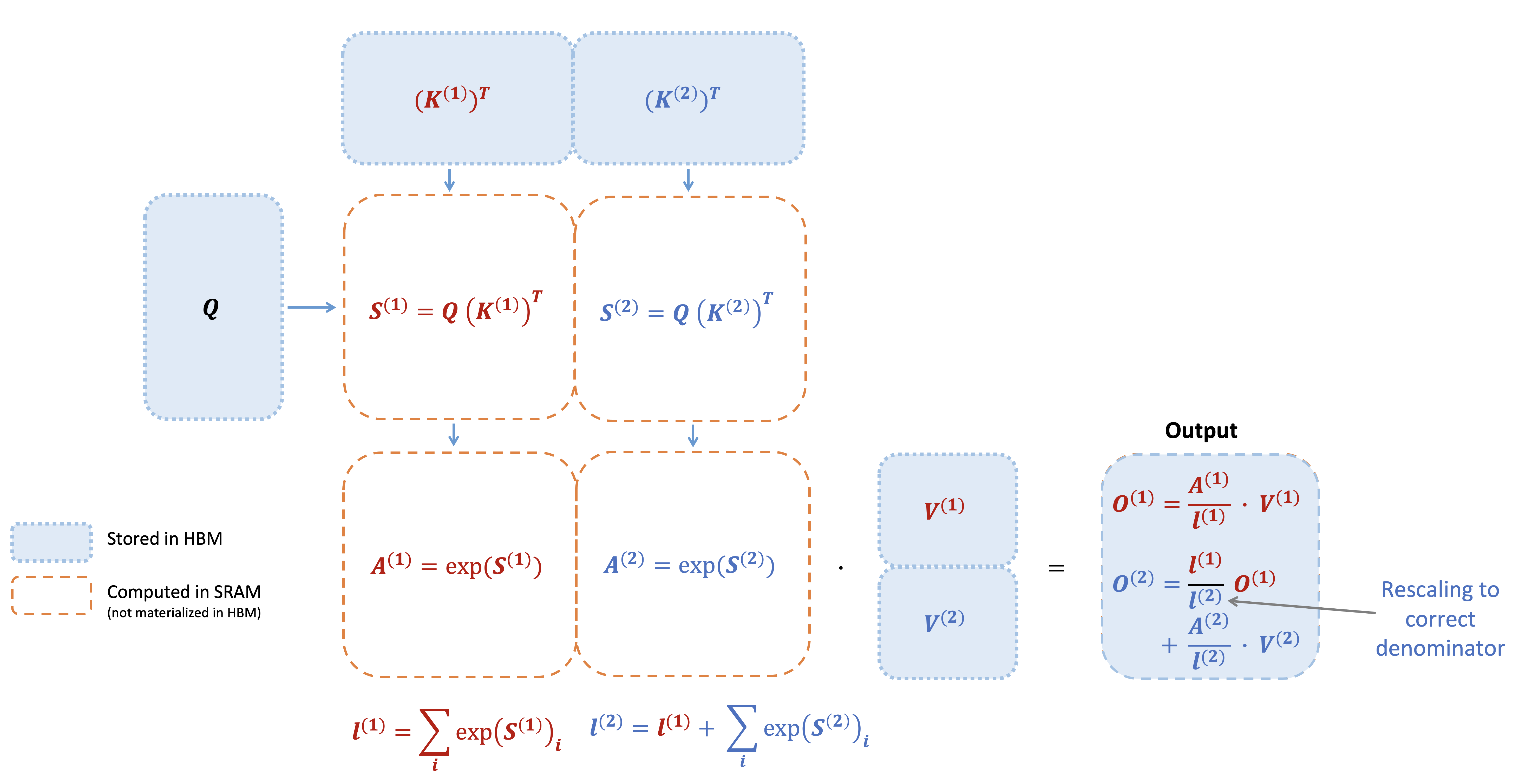
4. 在线 softmax 会针对每个块计算“局部”softmax，然后重新缩放以最终获得正确的输出(红色部分表示V1和V2区别)：

下图所示，展示了当K被分成两个块，V也被分成两个块时，FlashAttention前向传递的过程通过对每个块计算注意力并重新缩放输出，最终得到正确的答案，同时避免了中间矩阵S和P的昂贵内存读写(注意，图中省略了softmax中将每个元素减去行最大值的步骤)

3.1.2 Flash Attention2的前向传播算法

Flash Attention2完整的前向传递过程

V2相比V1，在前向传播层面进行了两个小的调整，以减少非矩阵乘法的FLOPs：

1. 不需要通过 diag(ℓ⁽²⁾)⁻¹ 重新调整输出更新的两个项：

O⁽²⁾ = diag(ℓ⁽¹⁾/ℓ⁽²⁾)⁻¹O⁽¹⁾ + diag(ℓ⁽²⁾)⁻¹e^{S(2) − m(2)}V⁽²⁾.

可以保留 O⁽²⁾ 的“未缩放”版本并保留统计数据 ℓ⁽²⁾：

仅在循环的每个结束时，才会将最后的 通过 diag(ℓ^(last))⁻¹ 缩放以获得正确的输出。

2. 不必同时保存最大值 m^(j) 和指数和 ℓ^(j) 以供反向传播。只需存储logsumexp   L^(j) = m^(j) + log (ℓ^(j))。

3. 在 2 个块的简单情况下，在线 softmax 技巧现在变成(红色部分表示V1和V2区别)：

通过例子说明如何分块计算softmax。对向量 [1, 2, 3, 4]计算softmax, 分成两块[1, 2]和[3, 4]进行计算。计算block 1:

计算block2，得出softmax结果:

3.2 Flash Attention V2 反向传播层面的改进

在标准注意力实现中, 后向传递计算Q, K, V的梯度时, 需要用到N × N的中间矩阵 S, P, 但这两个矩阵并没有保存下来。这里的技巧是重计算, 保存了两个统计量m(x), l(x), 后向传递时在高速的SRAM上快速地重新计算Attention, 通过分块的方式重新计算注意力矩阵 S, P。相比于标准注意力中, 从HBM中读取很大的中间注意力矩阵的方法, 重计算的方法要快得多。

总的来说, Flash Attention通过调整注意力的计算顺序, 引入两个额外的统计量进行分块计算, 避免了实例化完整的 N × N的注意力矩阵 S, P, 将显存复杂度从 O(N²)降低到了O(N)。另外, 对于内存受限的标准注意力, Flash Attention通过kernel融合和分块计算, 大量减少了HBM 访问次数, 尽管由于后向传递中的重计算增加了额外的计算量FLOPs, 减少了运行时间, 计算速度更快（GPT2的7.6倍）。

Flash Attention2的反向传播与Flash Attention几乎相同。 但对softmax中的行方向logsumexp 𝐿进行了微小的调整，而不是同时使用行方向的最大值和指数和。以下是FlashAttention2的反向传播完整流程：

3.3 并行化与Work Partitioning Between Warps

3.3.1 并行化下的前向传播与反向传播

FlashAttention的第一个版本在批量大小和头数上进行了并行化，使用 1 个线程块来处理一个注意力头，总共有批处理大小 ⋅ heads 数量 个线程块。

每个线程块都被安排在流式多处理器 (SM) 上运行，例如，A100 GPU 上有 108 个这样的 SM。当这个数字很大时（例如  ≥ 80），这种调度是有效的，因为我们可以有效地使用 GPU 上的几乎所有计算资源。

对于长序列（通常意味着小批量或少量头），为了更好地利用 GPU 上的多处理器，现在在序列长度维度上额外进行并行化。这为该方案带来了显着的加速。

• 前向传播

可以看到外循环（在序列长度上）是粗硬的并行，并且将将它们安排在不需要相互通信的不同线程块上。还在批处理维度和磁头数量维度上进行并行化，就像在FlashAttention中所做的那样。当批处理大小和磁头数量较小时，在序列长度上增加的并行性有助于提高占用率（正在使用的 GPU 资源的分数），从而在这种情况下提高速度。

这些交换循环顺序的想法（在原始的FlashAttention论文中，外循环在行块上，内循环在列块上），以及在序列长度维度上并行化的想法首先由 Phil Tillet 在 Triton 中提出并实现。

• 反向传播

不同列块之间唯一共享的计算是在Flash Attention V2 反向传播第15步中的更新 dQ 中，需要将 dQ_i 从 HBM 加载到 SRAM，然后在芯片上更新 dQ_i ← dQ_i + dS_i^(j)K_j，并写回 HBM。因此，也在序列长度维度上并行化，并为后向传递的每个列块安排 1 个线程块。使用原子添加在不同的线程块之间进行通信以更新 dQ。

最终，如下图所示

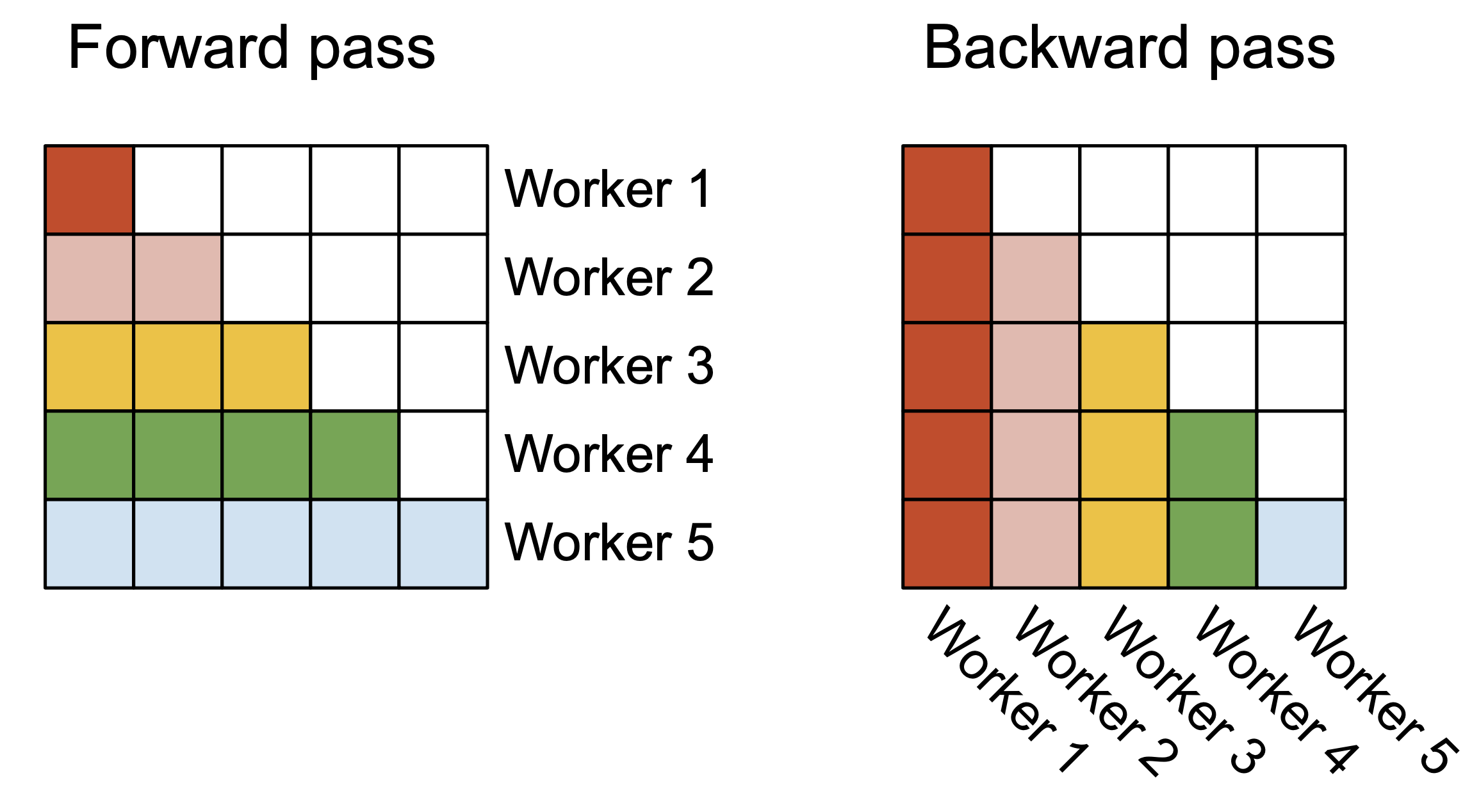
1. 在前向传递(左侧)中，将工作线程(线程块)并行化，其中每个工作线程负责处理注意力矩阵的“行块”
2. 在后向传递(右侧)中，每个工作线程负责处理注意力矩阵的“列块”

3.3.2 Work Partitioning Between Warps

正如上一节所描述的如何调度线程块，即使在每个线程块内，也必须决定如何在不同的 warp 之间划分工作。通常每个线程块使用 4 或 8 个 warp，具体划分如下图所述：

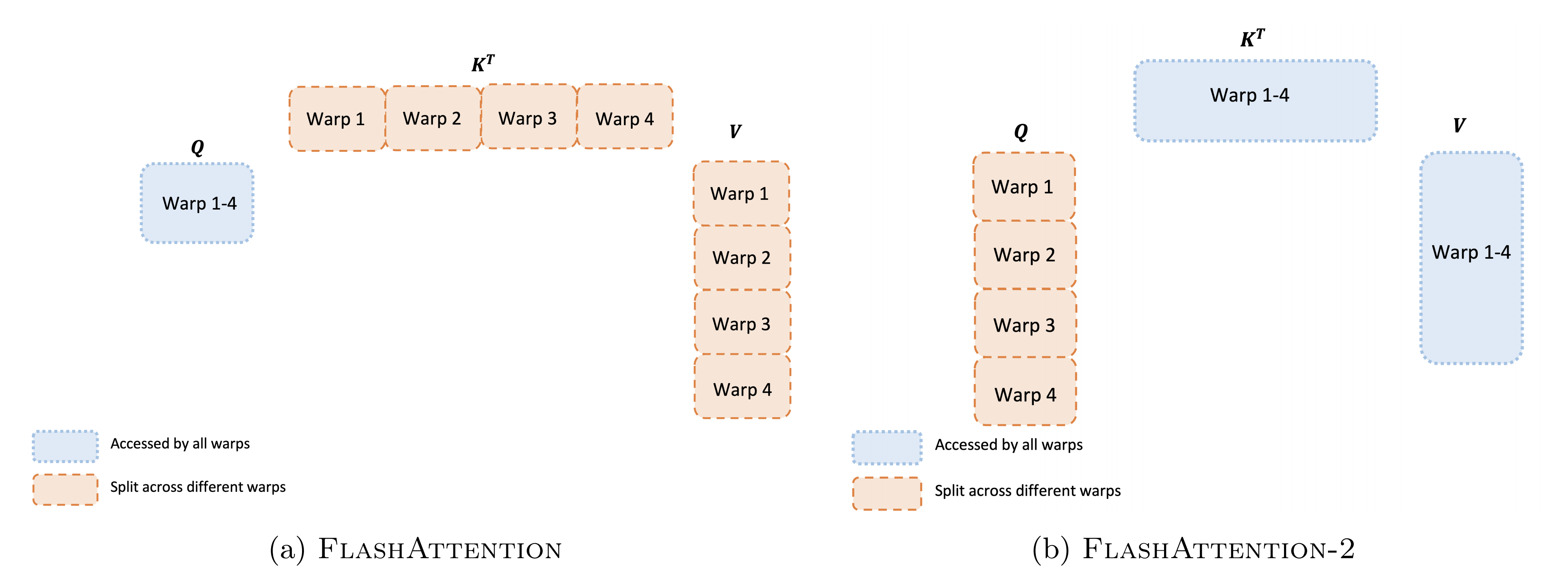
• 前向传播

对于每个块，Flash Attention将 K 和 V 拆分到 4 个 warp 中，同时保持 Q 可供所有 warp 访问。每个 warp 相乘以获得 QK^⊤ 的一个切片，然后它们需要与 V 的一个切片相乘并进行通信以将结果相加。这被称为 ``split-K’’ 方案。但是，这是低效的，因为所有 warp 都需要将其中间结果写入共享内存，进行同步，然后将中间结果相加。这些共享内存读写会减慢Flash Attention中的前向传递速度。

在Flash Attention2中，将 Q 拆分到 4 个 warp 中，同时保持 K 和 V 可供所有 warp 访问。在每个 warp 执行矩阵乘法以获得 QK^⊤ 的一个切片后，它们只需与它们的共享 V 切片相乘即可获得其相应的输出切片。不需要在 warp 之间进行通信。共享内存读/写的减少可以提高速度。

• 反向传播

类似地，对于反向传播，选择对 warp 进行分区以避免“split-K”方案。但是，由于所有不同输入和梯度 Q, K, V, O, dO, dQ, dK, dV 之间的依赖关系更为复杂，因此它仍然需要一些同步。尽管如此，避免“split-K”可以减少共享内存的读写，并再次提高速度。

• 调整块大小

增加块大小通常会减少共享内存的加载/存储，但会增加所需的寄存器数量和共享内存的总量。超过某个块大小后，寄存器溢出会导致速度明显减慢，或者所需的共享内存量大于 GPU 可用的内存量，内核根本无法运行。通常，选择大小为 {64, 128} × {64, 128} 的块，具体取决于头部尺寸 d 和设备共享内存大小。手动调整每个头部尺寸，因为块大小基本上只有 4 种选择，但这可以从自动调整中受益，以避免这种手动劳动。

四、Flash Decoding

在训练过程中，FlashAttention对batch size和query length进行了并行化加速。而在推理过程中，query length通常为1，这意味着如果batch size小于GPU上的SM数量（例如A100上有108个SMs），那么整个计算过程只使用了GPU的一小部分！特别是当上下文较长时，通常会减小batch size来适应GPU内存。例如batch size = 1时，FlashAttention对GPU利用率小于1%！

FlashAttention

在FlashAttentionz中O⁽²⁾的计算依赖于O⁽¹⁾。从下图也可以看出，FlashAttention是按顺序更新output的，其实当时我在看FlashAttention这篇文章时就觉得这个顺序操作可以优化的，因为反正都要rescale，不如最后统一rescale，没必要等之前block计算完（为了获取上一个block的max值）。

Flash-Decoding

上面提到FlashAttention对batch size和query length进行了并行化加速，Flash-Decoding在此基础上增加了一个新的并行化维度：keys/values的序列长度。即使batch size很小，但只要上下文足够长，它就可以充分利用GPU。与FlashAttention类似，Flash-Decoding几乎不用额外存储大量数据到全局内存中，从而减少了内存开销。

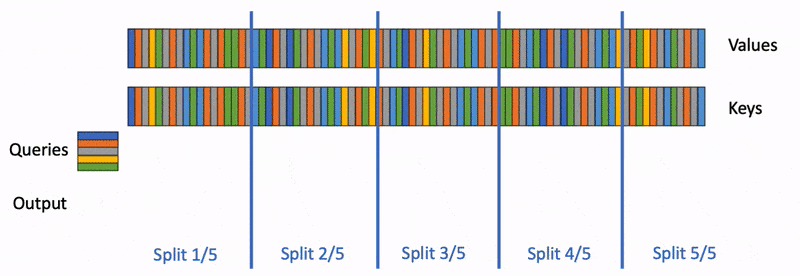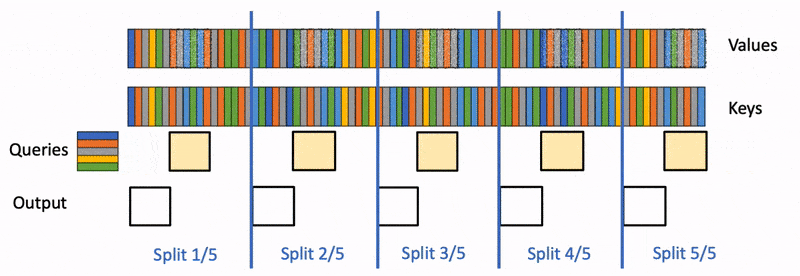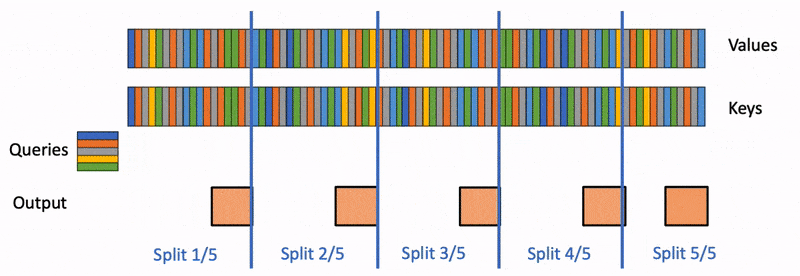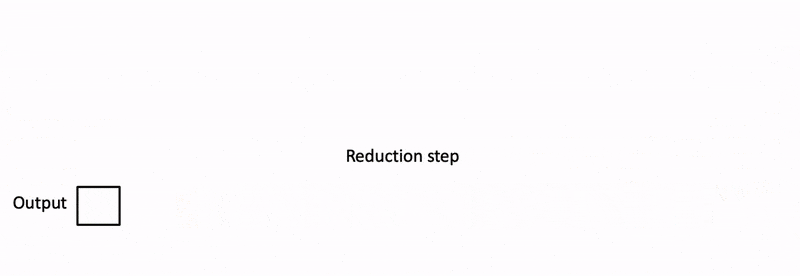
Flash Decoding主要包含以下三个步骤（可以结合上图来看）：

1. 将keys和values分成较小的block
2. 使用FlashAttention并行计算query与每个block的注意力（这是和FlashAttention最大的区别）。对于每个block的每行（因为一行是一个特征维度），Flash Decoding会额外记录attention values的log-sum-exp（标量值，用于第3步进行rescale）
3. 对所有output blocks进行reduction得到最终的output，需要用log-sum-exp值来重新调整每个块的贡献

实际应用中，第1步中的数据分块不涉及GPU操作（因为不需要在物理上分开），只需要对第2步和第3步执行单独的kernels。虽然最终的reduction操作会引入一些额外的计算，但在总体上，Flash-Decoding通过增加并行化的方式取得了更高的效率。

Using Flash-Decoding

1. FlashAttention2.2及之后的版本
2. xFormers0.0.22及之后的版本xformers.ops.memory_efficient_attention模块
3. FlashAttention提供了LLaMa v2/CodeLLaMa的例子(未实现)。此外，xformers提供了一个针对LLaMa v1/v2的小示例。

五、Flash Decoding++

5.1 简介

LLM推理中的主要操作如下图所示：linear projection(①和⑤)、attention(②、③和④)和feedforward network(⑥)。为简单起见，这里忽略了position embedding、non-linear activation、mask等操作。将LLM推理时对Prompt的处理过程称为预填充阶段(Prefill phase)，第二阶段预测过程称为解码阶段(Decode phase)。这两个阶段的算子基本一致，主要是输入数据的shape是不同的。由于解码阶段一次只处理一个令牌（batch size=1，或batch size很小），因此输入矩阵是flat-shape matrices（甚至是vectors），参见下图解码阶段部分中和KV Cache拼接的红色向量。

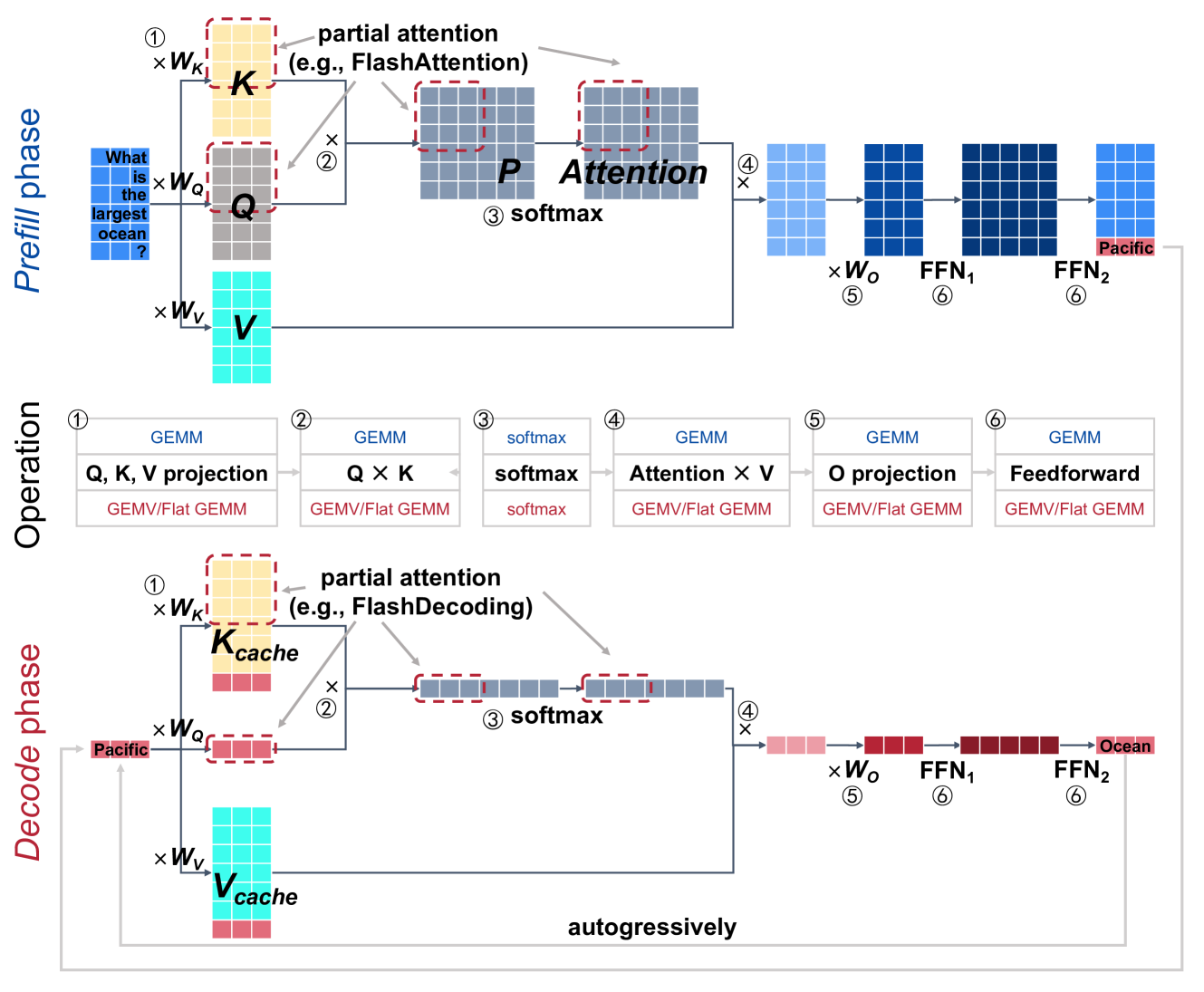
上图显示了 LLM 推理的主要数据流，其中预填充阶段和解码阶段都有一个Transformer层。Transformer可以分为flat GEMM（通用矩阵乘法）操作（例如 K, Q, V, O 权重投影和前馈）和注意力/softmax 计算。对于注意力计算，对注意力矩阵中的一行采用 softmax 操作。 1. 为了提高并行性，FlashAttention将注意力矩阵划分为较小的图块，行也被拆分以计算partial softmax 结果。当计算新的partial softmax 结果时，采用同步 softmax 操作来更新先前的partial softmax 结果。论文作者在 NVIDIA Tesla A100 GPU 上以 1024 输入长度进行的分析，这种同步partial softmax 更新占 Llama2-7B 推理注意力计算的 18.8%，这导致了加速 LLM 推理的第一个挑战。 2. 在解码阶段，flat GEMM 操作的计算资源利用不足。由于解码阶段按顺序生成 token，flat GEMM 操作趋向于扁平形状（当批量大小为 1 时甚至会变成 GEMV（通用矩阵-向量乘法）操作）。对于小批量（例如 8），以前的设计（例如 cuBLAS、CUTLASS 等）是用零填充矩阵以执行更大尺寸（例如 64）的 GEMM，导致计算利用率不足 50% 以上。 3. 考虑到输入动态和硬件配置，LLM 推理的性能受到静态数据流的影响。例如，小批量使得 LLM 推理的解码阶段受内存限制，而大批量使得其受计算限制。单一静态的数据流可能会导致 LLM 推理中不同形状的 GEMM 性能损失 50.25%。

针对上述挑战，FlashDecoding++地提出：

1. Asynchronized softmax with unified max value.FlashDecoding++ 利用统一的最大值来进行不同的partial softmax 计算。每个partial softmax 结果可以单独处理，无需同步更新。
2. Flat GEMM optimization with double buffering.FlashDecoding++仅将矩阵大小填充为8，而不是之前针对Flat GEMM的设计中的64，以提高计算利用率。FlashDecoding++指出不同形状的Flat GEMM面临不同的瓶颈，并通过双缓冲等技术进一步提高内核性能。
3. Heuristic dataflow with hardware resource adaption.FlashDecoding++ 同时考虑输入动态和硬件配置，并为 LLM 推理数据流动态应用内核优化。

下图展示了以上3种方法的示意图：

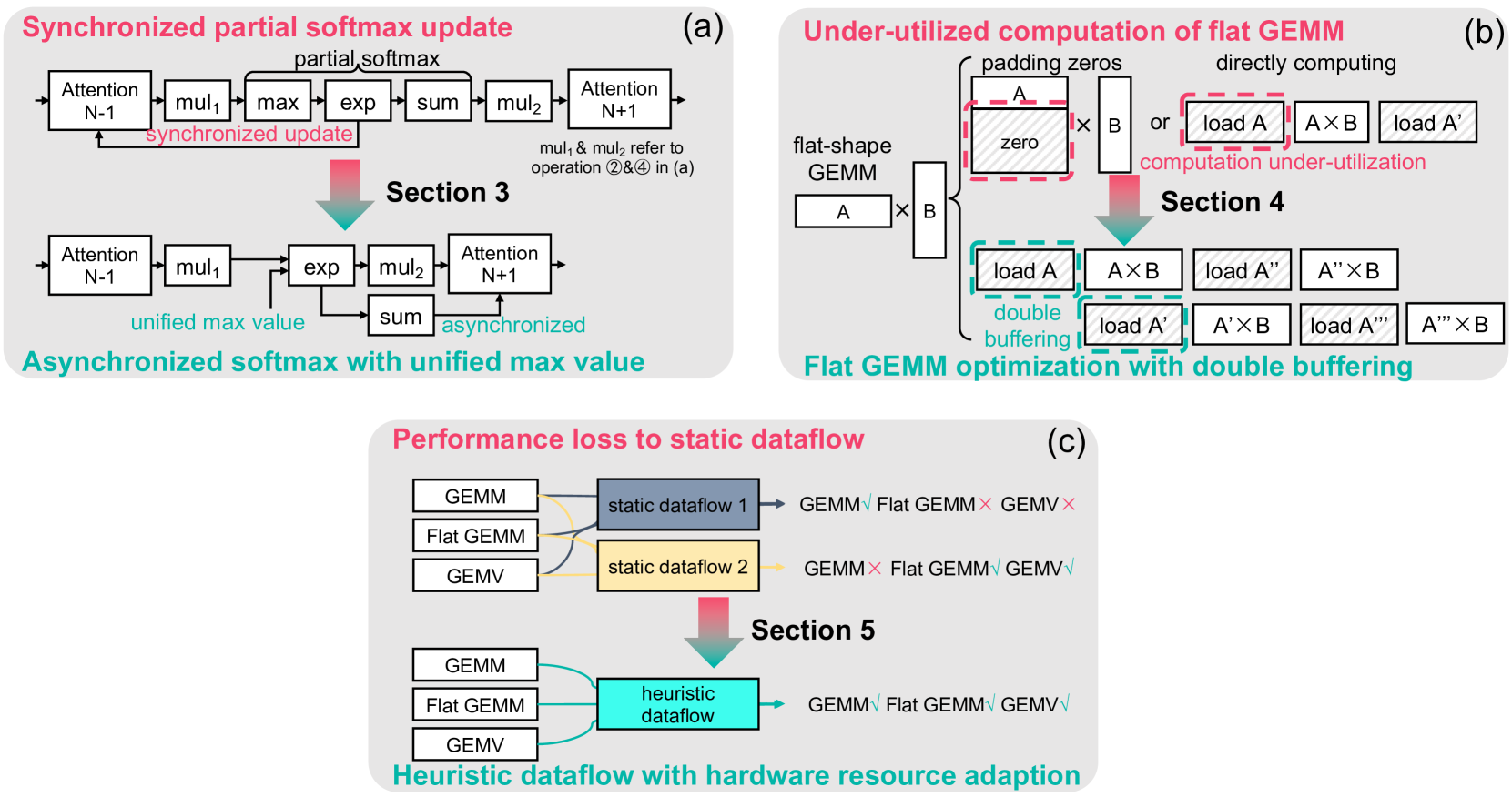
5.2 Asynchronized Softmax with Unified Maximum Value

不同 softmax 计算方案的比较。 (a) 整个向量的 Softmax 计算。 (b)计算每个部分向量的部分softmax，并且所有部分softmax结果需要同步更新操作。 (c)使用统一的最大值计算部分softmax，并且每个部分向量单独处理，没有同步更新。

上图(a) 中所示的 softmax 操作需要先计算并存储所有全局数据，然后才能继续。这会导致内存消耗高且并行性低。FlashAttention提出了partial softmax 技术来减少内存消耗，FlashDecoding提高并行性。(b) 展示了partial softmax 操作的示意图。其主要思想是将向量 x 分成部分向量（*即} x^′ 和 x^″）。x^′ 和 x^″ 的partial softmax 结果按照图中(a)分别计算，然后彼此同步更新。此同步更新的详细计算如下公式所示。通过partial softmax 的实现，可以实现计算的高效并行性，同时降低注意力计算的内存成本。

由于部分softmax需要根据其他部分softmax结果进行更新，因此不可避免地引入了数据同步操作。需要同步的原因在于每个部分向量的最大值不同。使用最大值来避免指数运算溢出（f(x)），并将指数相加（l(x)）作为分母的softmax操作。这种对每个部分最大值的非线性操作使得每个部分softmax计算之间的同步不可避免。

为了去除同步操作，论文中提出找到一个合适的公共最大值ϕ。对于 x_i ≫ ϕ 的情况，e^{x_i − ϕ} 溢出，无法使用固定宽度的浮点数表示。对于另一种 x_i ≪ ϕ 的情况，e^{x_i − ϕ} → 0，导致精度损失。因此，应仔细选择合适的缩放因子 ϕ 以避免上述两种情况。下图显示了具有不同输入的典型 LLM 中 x_i（softmax 输入向量中的元素）的统计分布。。具体来说，对于 Llama2-7B，当 x_i 时，有 −16.8 < x_i < 6.5。由于 e^b − a 和 e^a − b 可以用 float32 格式表示，因此可以在上边公式中设置 ϕ = a。

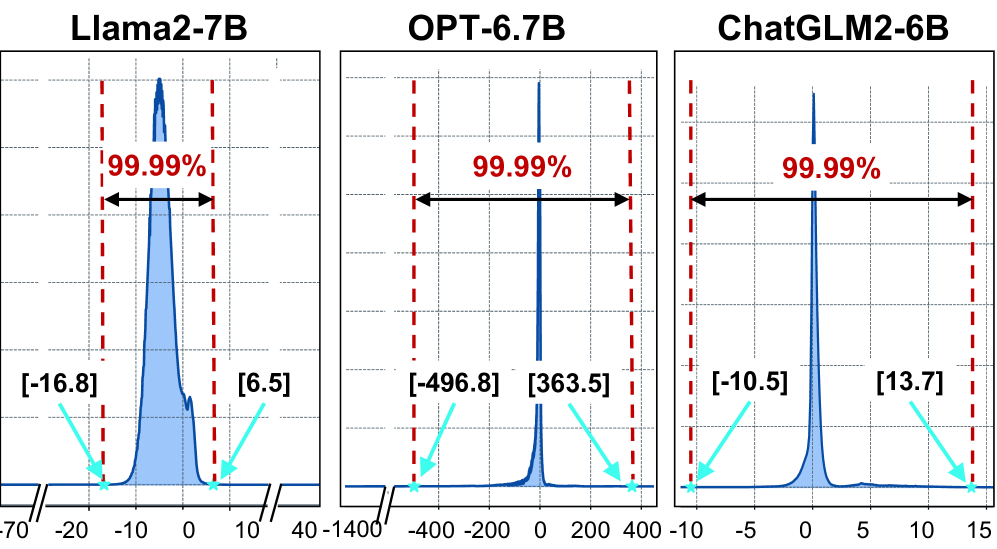
但是对于OPT-6.7B来说，其范围较大，可以采用动态调整策略，如果在推理过程中发现设置的ϕ 不合理，那么就终止当前操作，然后采用FlashAttention和FlashDecoding的方法计算softmax。下图b中展示当e^9 − 6超过阈值e³时的recompution过程。

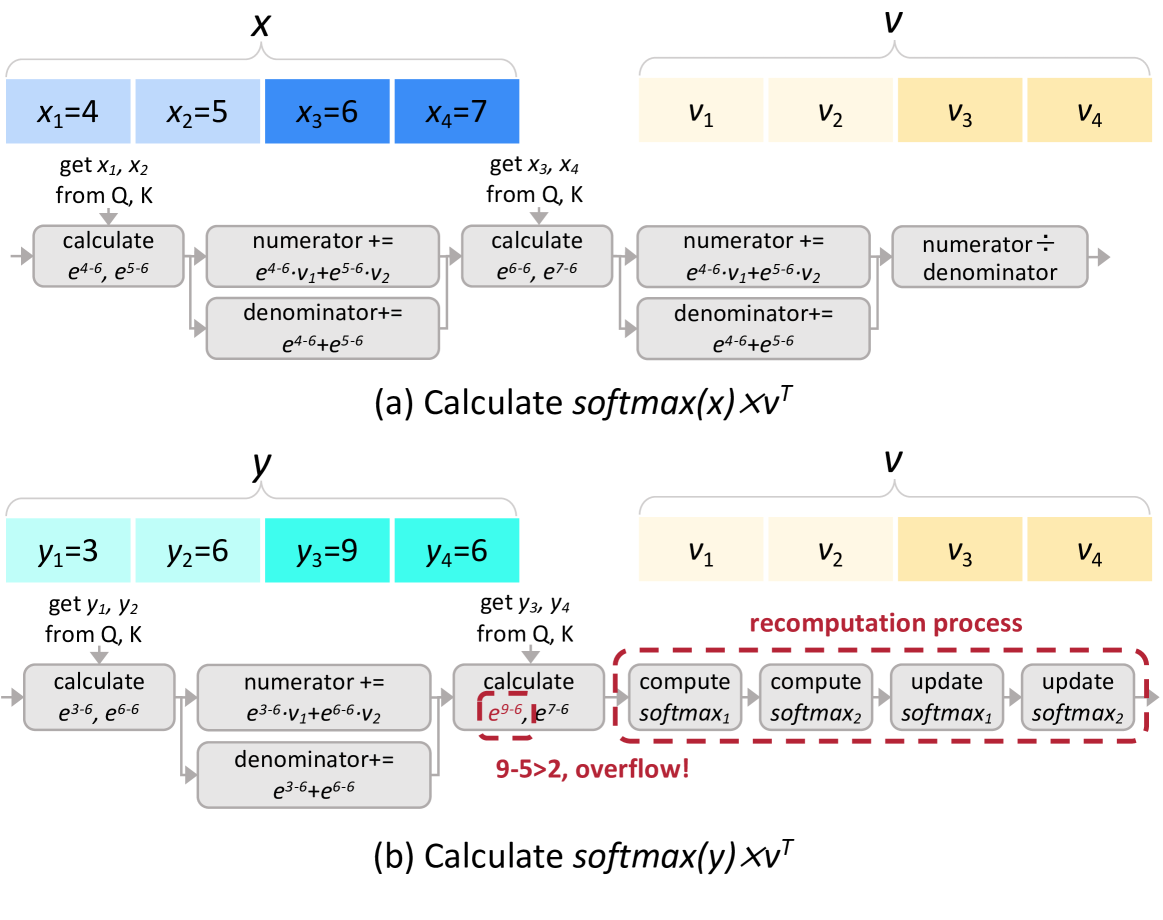
异步partial softmax 计算示例。 (a) 每个partial softmax 结果都是单独处理的，没有同步更新。 (b) 当发生溢出时，需要对所有 parital softmax 计算进行重新计算过程。

5.3 Flat GEMM Optimization with Double Buffering

decode阶段的过程主要由 GEMV（batch size=1）或平坦 GEMM（batch size > 1）操作组成。GEMV/GEMM 操作可以使用 M, N, K 表示，其中两个相乘矩阵的大小为 M × K 和 K × N。以前的 LLM 推理引擎利用 Tensor Core 通过 cuBLAS和 CUTLASS等库来加速这些操作。尽管现代 Tensor Core 架构适合处理 M = 8 的 GEMM，但这些库为了隐藏memory latency,通常将 M 维度平铺为 64。但是，对于 decode 阶段的 GEMV 或flat GEMM 操作，通常 M ≪ 64，于是填充0到64，导致计算利用率低下。

假设 N− 维和 K− 维的tiling size分别为 B_N 和 B_K。每个GEMM tile的计算量为 2 × M × B_N × B_K，总共 个GEMM tiles。总内存访问量为 (M × B_K + B_N × B_K) × B + M × N。因此，计算/内存比率为：

另一方面，并​​行度为 。于是发现了GEMV或falt GEMM两者矛盾之处：计算和内存比与B_N 呈正相关，而并行度与 B_N 呈负相关。下图描绘了具有不同 N 和 B_N 的flat GEMM 的归一化性能。总结了两个关键结论： 1. 对于较小的 N，flat GEMM是parallelism-bounded。NVIDIA Tesla A100 中有 108 个流多处理器 (SM)。于是应该将 设置为一个相关的常数（例如 128 或 256），这与硬件并行度（SM 数量）有关。 2. 对于较大的 N，flat GEMM是memory-bounded。通过隐藏memory access latency可以提高性能。

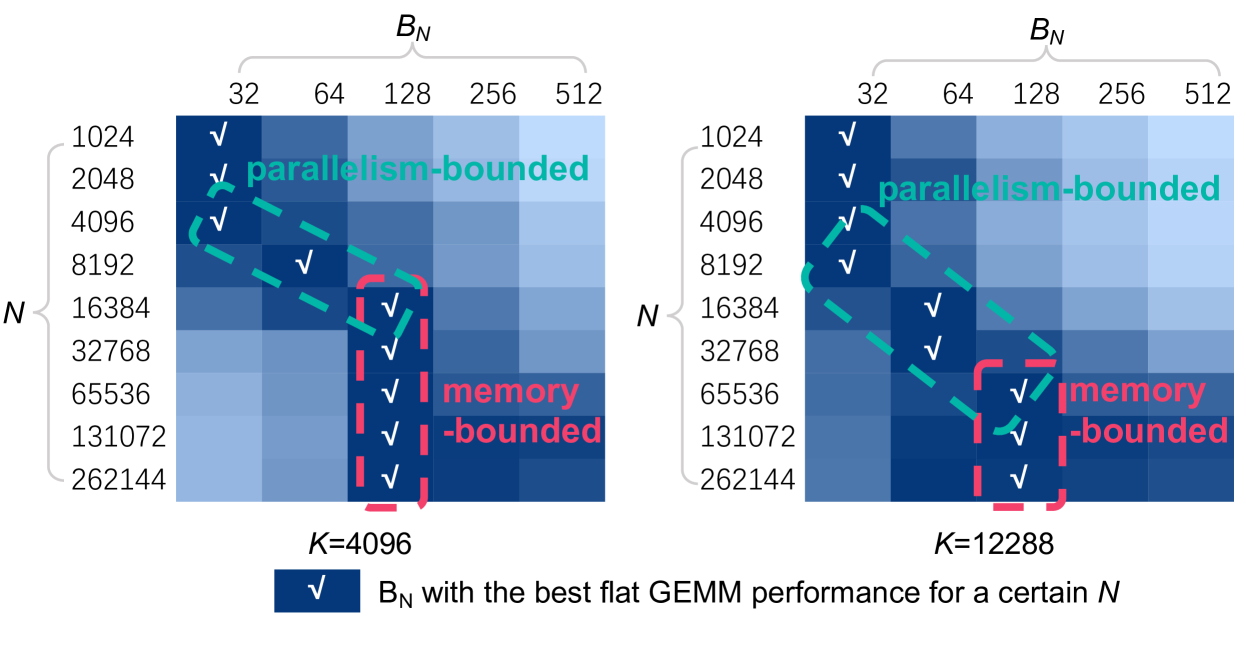
为了隐藏memory access latency，FlashDecoding++引入了double buffering技术。具体来说就是在共享内存中分配两个buffer，一个buffer用于执行当前tile的GEMM计算，同时另一个buffer则加载下一个tile GEMM所需的数据。这样计算和内存访问是重叠的，在N较大时采取这种策略，下图为示意图。

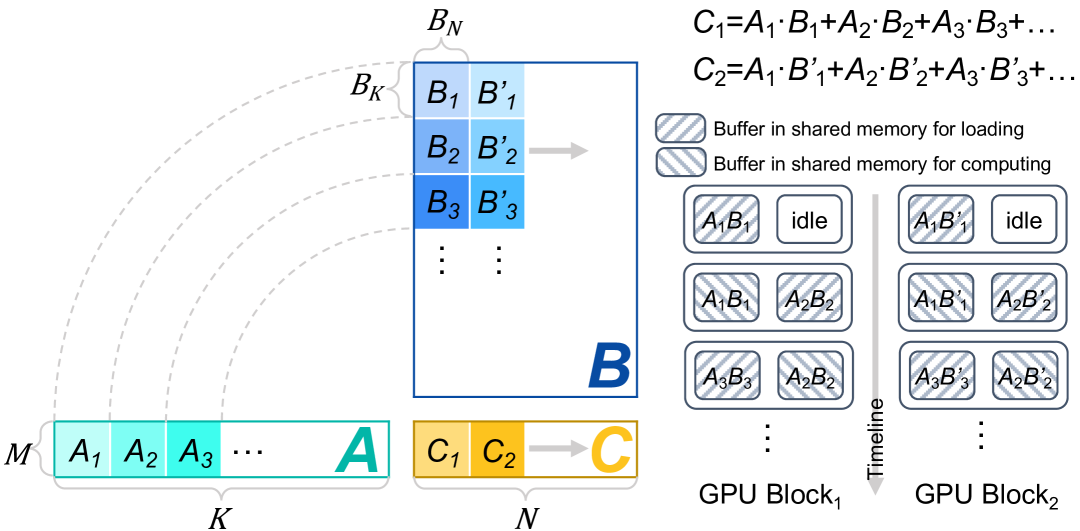
上图显示了使用double buffering的flat GEMM 优化示例。对于 M < 8，考虑到现代 Tensor Core 架构，首先将 M− 维度填充为 8。K− 维度中的工作负载在一个 GPU 块内处理（例如 A₁​​, A₂, A₃, ...），而 N− 维度中的工作负载使用不同的 GPU 块并行处理（例如 C₁, C₂, ...）。我们以 GPU Block₁ 为例，K− 维度中每个矩阵的第一个图块（即 A₁​​ 和 B₁）被加载到共享内存中的左缓冲区。然后，在 A₁​​ 和 B₁ 之间执行 GEMM 操作。因此，A₂ 和 B₂ 被加载到共享内存中的右侧缓冲区。

5.4 Heuristic Dataflow with Hardware Resource Adaption

在LLM推理场景中，有多种因素影响线性工作负载的实现性能：（a）输入动态。批量大小和输入序列长度的变化带来了动态工作负载。 (b) 模型多样性。线性工作负载随模型结构和大小的不同而变化。 (c) GPU 容量。实现之间的相对性能随 GPU 特性而变化，例如内存带宽、缓存大小和计算能力。 (d) 工程影响。工程工作也极大地影响了内核性能。所有这些影响因素构建了一个巨大的搜索空间，使得在线性工作负载和相应的最佳实现之间生成有效的映射变得非常重要。

虽然这些因素构建了一个很大的搜索空间，但LLM中不同layer的同质性大大减少了算子优化的搜索空间。下图展示了 prefill 阶段和 decode 阶段的四个 GEMV/GEMM 操作，即 K, Q, V 投影、O 投影和两个前馈操作。每个 GEMV/GEMM 操作都可以抽象为 (M × K) 形矩阵与 (K × N) 形矩阵之间的乘法。对应了四种 [K, N] 组合。此外，M 仅与 prefill 阶段的输入序列长度和批量大小以及 decode 阶段的批量大小有关。下图(a) 显示了 LLM 推理中 GEMV/GEMM 运算的有限形状。

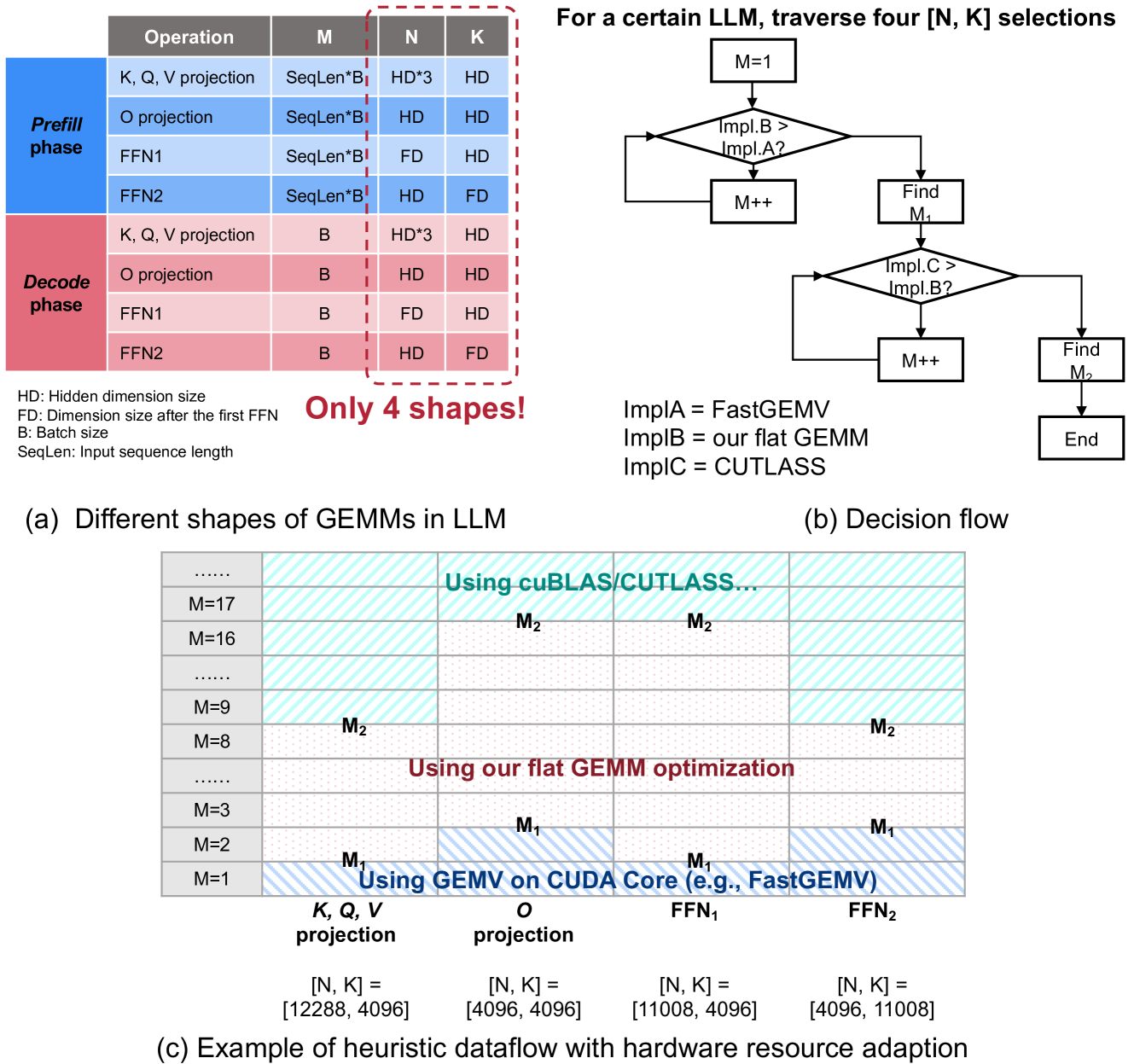
FlashDecoding++ 中具有硬件资源自适应的启发式数据流。

决策流程。因为对于某个 LLM 来说只有四种 [K, N] 形状，所以当 M 变化时，使用三种类型的 GEMV/GEMM 操作实现：用于 GEMV 和flat GEMM 操作的 FastGEMV（ImplA）、FlashDecoding++的flat GEMM优化（ImplB）以及针对传统 GEMM 优化的 CUTLASS库（ImplC）。因此，重要的是决定是否在较小的 M 下应用 ImplA 或 ImplB，以及在较大的 M 下应用 ImplB 或 ImplC。上图(b) 显示了决策流程。针对某个 M 分析 ImplA 和 ImplB 的性能，并增加 M 以找到拐点 M₁，其中 ImplB 的性能优于 ImplA。类似地发现另一个拐点 M₂，其中 ImplC 的性能优于 ImplB。请注意，每个 [N, K] 都有其各自的 M₁ 和 M₂。

启发式数据流。对于运行时 LLM 推理，当 M < M₁ 时，采用使用 CUDA Core 的 ImplA，当 M₁ ≤ M < M₂/M₂ ≤ M 时，采用使用 Tensor Core 的 ImplB/ImplC。请注意，决策流程是离线执行的，它不会影响运行时 LLM 推理的性能。

上图(c) 展示了将启发式数据流应用于 Llama2-7B 模型的示例。四种 [N, K] 形状分别为：K, Q, V 投影的 [12288, 4096]、O 投影的 [4096, 4096]、FFN 的 [11008, 4096] 和 [4096, 11008]。对于每个 [N, K]，基于图(c)中的决策流找到拐点。然后，形成查找表，并在运行时根据相应的实现执行每个 GEMV/GEMM 操作。在此示例中，当 decode 阶段的批量大小 = 1（M = 1）时，采用 FastGEMV 进行 K, Q, V 投影，并且当批量大小 = 1/输入序列长度 = 8 且 FFN₁（M = 8）时，应用FlashDecoding++的flat GEMM 优化。

参考

1. Efficient Memory Management for Large Language Model Serving with PagedAttention
2. vLLM Paged Attention
3. vLLM: Easy, Fast, and Cheap LLM Serving with PagedAttention
4. LLM 高速推理框架 vLLM 源代码分析 / vLLM Source Code Analysis
5. vLLM皇冠上的明珠：深入浅出理解PagedAttention CUDA实现
6. PageAttention代码走读
7. LLM（十七）：从 FlashAttention 到 PagedAttention, 如何进一步优化 Attention 性能
8. FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
9. 通透理解FlashAttention与FlashAttention2：全面降低显存读写、加快计算速度
10. FlashAttention:加速计算,节省显存, IO感知的精确注意力
11. SELF-ATTENTION DOES NOT NEED O(n²) MEMORY
12. ELI5: FlashAttention ELI5：FlashAttention
13. FlashAttention：具有 IO 感知，快速且内存高效的新型注意力算法
14. FlashAttention图解（如何加速Attention）
15. FlashAttention2详解（性能比FlashAttention提升200%）
16. 图解大模型计算加速系列：Flash Attention V1，从硬件到计算逻辑
17. 图解大模型计算加速系列：Flash Attention V2，从原理到并行计算
18. 图解大模型计算加速系列：Flash Attention V1，从硬件到计算逻辑
19. LLM（十七）：从 FlashAttention 到 PagedAttention, 如何进一步优化 Attention 性能
20. Flash Attention论文解读
21. FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning
22. Flash-Decoding for long-context inference
23. FlashAttenion-V3: Flash Decoding详解
24. FLASHDECODING++: FASTER LARGE LANGUAGE MODEL INFERENCE ON GPUS
25. 【FlashAttention-V4，非官方】FlashDecoding++
26. 大模型推理加速之FlashDecoding++：野生Flash抵达战场