EM算法
1.基础知识
1.1.高斯混合模型
高斯混合模型是有如下形式的概率分布模型:
其中 πk > 0
为混合系数,
假设观测数据 x1, x2, ⋯, xn ∈ R 由 K 个组分的高斯混合模型生成。
高斯混合分布的对数最大化似然函数为:
对数里面有加和,无法直接通过求偏导解方程的方法求取最大值。 可以用EM算法解决这种难以计算的问题,EM算法是一种近似逼 近的迭代计算方法。
1.2.全概率公式
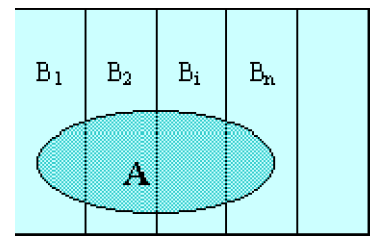
对于任一事件 A
,若有互不相容的事件 Bk, k = 1, ⋯, K
且
上式称为全概率公式。
1.3.Jensen不等式
如果 f 是凸函数, X是随机变量,那么 E[f(X)] ≥ f(EX) ,如果 f 是凹函数, X是随机变量,那么 E[f(X)] ≤ f(EX) ,如果 f 是严格凹或凸函数, 那么 E[f(X)] = f(EX) 当且仅当 p(x = E[X]) = 1 ,也就是 X 是常量。如下图:

2.EM算法原理及推导
实际问题中可能有一些数据是我们无法观测到的,假设观测数据X = {x1, ⋯, xn},缺失数据Z = {z1, ⋯, zn},观测数据与缺失数据组合成完整数据Y = {y1, ⋯, yn},模型的参数 θ 有待估计。其中缺失数据 Z 由 K 个分布组成,这 K 个分布的参数可能不同,每个观测数据 xi 来自于这 K 个分布其中之一。这就造成观测数据下的似然函数难以求得解析解,即 L(θ|X) = P(X|θ) 难以求解。但是完全数据下的似然函数 L(θ|Y) = P(Y|Y) 容易求解,观测数据条件下的隐变量概率 P(Z|X, θ) 容易求得。
EM算法
对于观测数据 X
样例间独立,我们想找到每个样例隐含的类别(分布) z,能使得 p(x, z)
最大.对于每个样例 xi 假设 Qi
是关于隐含变量 z
的概率分布,则
根据Jensen不等式,想要等式成立,有如下条件:
可以推出:
则:
即 Qi 为在给定 xi, θ(t) 情况下 xi 属于分类 z 的概率。将 Qi带入可得:
上式中第二项与 θ 无关为常数项(熵),令:
Q(θ|θ(t)) = ∑zp(z|X, θ(t))ln P(X, z|θ) = Ez(ln P(X, z|θ)|X, θ(t))
可得最大化似然函数等同于:
arg maxθ𝓁(θ|X) ⇔ arg maxθQ(θ|θ(t))
EM算法流程
由以上推导可知EM算法通过迭代求 𝓁(θ|X) = ln P(X|θ) 的最大似然估计,每次迭代步骤如下:
(1)选择参数的初始值 θ(0) 开始迭代
(2)E步(求期望):
Q(θ|θ(t)) = ∑zp(z|X, θ(t))ln P(X, z|θ) = Ez(ln P(X, z|θ)|X, θ(t))
(3)M步:最大化第二步的期望值,然后对参数求偏导等于0后求得下一步迭代的参数:
θ(t + 1) ← arg maxθQ(θ|θ(t))
(4)重复E步和M步直至:
∥θ(t + 1) − θ(t)∥ > ε1 or ∥Q(θ(t + 1)|θ(t)) − Q(θ(t)|θ(t))∥ > ε2
停止迭代,返回 θ* = θ(t + 1) .
EM算法是利用下边界逼近真实值,如下图:

𝓁(θ|X) ≥ ∑zp(z|X, θ(t))ln P(X, z|θ) + ( − ∑zp(z|X, θ(t))ln P(z|X, θ(t))) ≜ g(θ|θ(t))
3.EM算法收敛性
观测数据的似然函数:
Q(θ|θ(i)) = ∑ZP(Z|X, θ(i))ln P(X, Z|θ)
令
H(θ|θ(i)) = ∑ZP(Z|X, θ(i))ln P(Z|X, θ)
则对数似然函数可以写成:
ln P(X|θ) = Q(θ|θ(i)) − H(θ|θ(i))
ln P(X|θ(i + 1)) − ln P(X|θ(i)) = [Q(θ|θ(i + 1)) − Q(θ|θ(i))] − [H(θ|θ(i + 1)) − H(θ|θ(i))]
由于 θ(i + 1) 使 Q(θ|θ(i)) 达到极大,所以有
Q(θ|θ(i + 1)) − Q(θ|θ(i)) ≥ 0
第二项:
因此 P(X|θ) 是单调递增的,且有上界,因此收敛。
4.EM算法在高斯混合模型中的应用
高斯混合模型在第一节中已经提过,下面以单变量为例。
明确隐变量,写出完整的对数似然函数
完整数据可表示为 (xi, γi1, ⋯, γiK)
完整数据的似然函数可表示为:
E-步
M-步
θ(t + 1) = arg maxθQ(θ|θ(t))
多元高斯混合模型
与单元求解类似(注意向量和矩阵求导的细节即可)