Hyper-Connections

一、简介

Transformer中残差连接主要就两种变体Pre-Norm 和 Post-Norm各自都有其局限性，这里苏剑林的博客有过分析。

Pre-Norm：在每个残差块之前做Norm，能够有效地减少梯度消失问题。Pre-Norm的问题在于后面的层的输出太像，以至于削弱了模型的学习能力。
Post-Norm：在残差块之后做norm，有助于减少表示崩溃问题，但也会重新引入梯度消失问题。

Hyper-Connections的灵魂在于通过动态调整不同层之间的连接权重，弥补了残差连接在梯度消失（Gradients Vanishing）和表示崩溃（representation collapse）之间的跷跷板现象。最后发现，不仅训练比Pre-Norm稳定，层间相似度更低，相似度范围更广，效果更好。

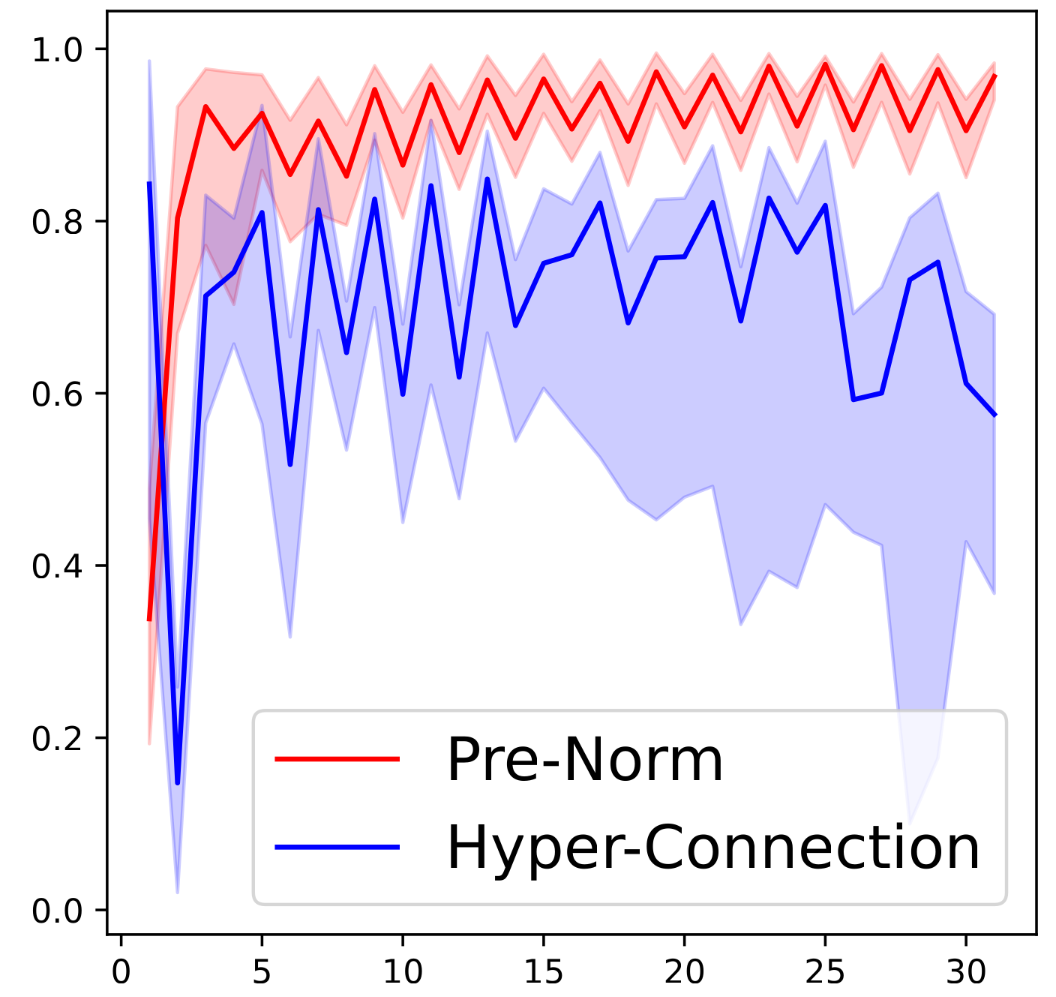
二、方法

Hyper-Connections引入了可学习的深度连接（depth-connections）和宽度连接（width-connections）。包含两种维度的连接，遂命名为Hyper-Connections。下面有分析说明，这不仅使得模型能够动态调整不同层之间的连接强度，甚至能重新排列网络层次结构。

2.1 Hyper-connections

2.1.1 深度连接与宽度连接

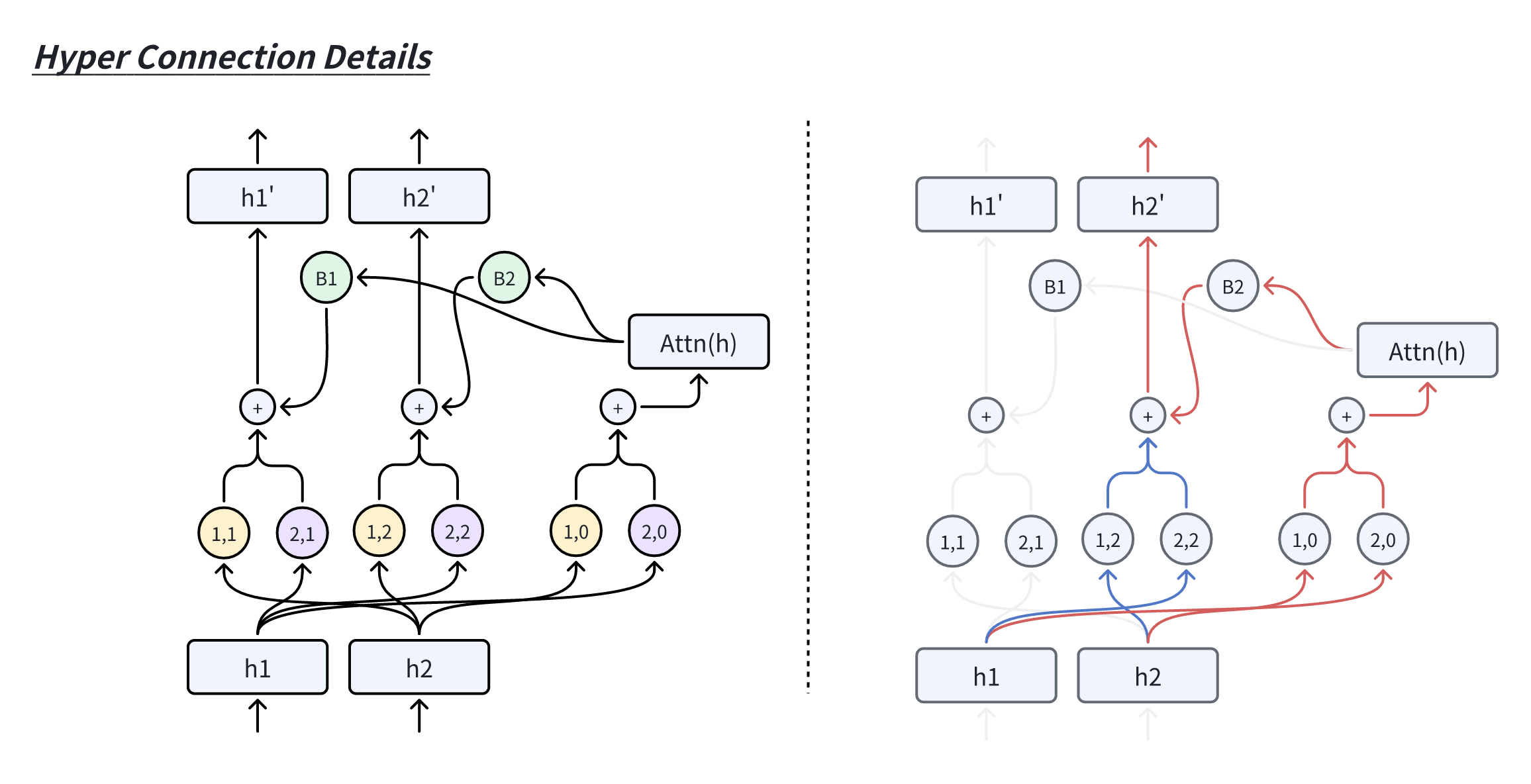
Hyper-Connections在Transformer上完整的网络结构图如下：

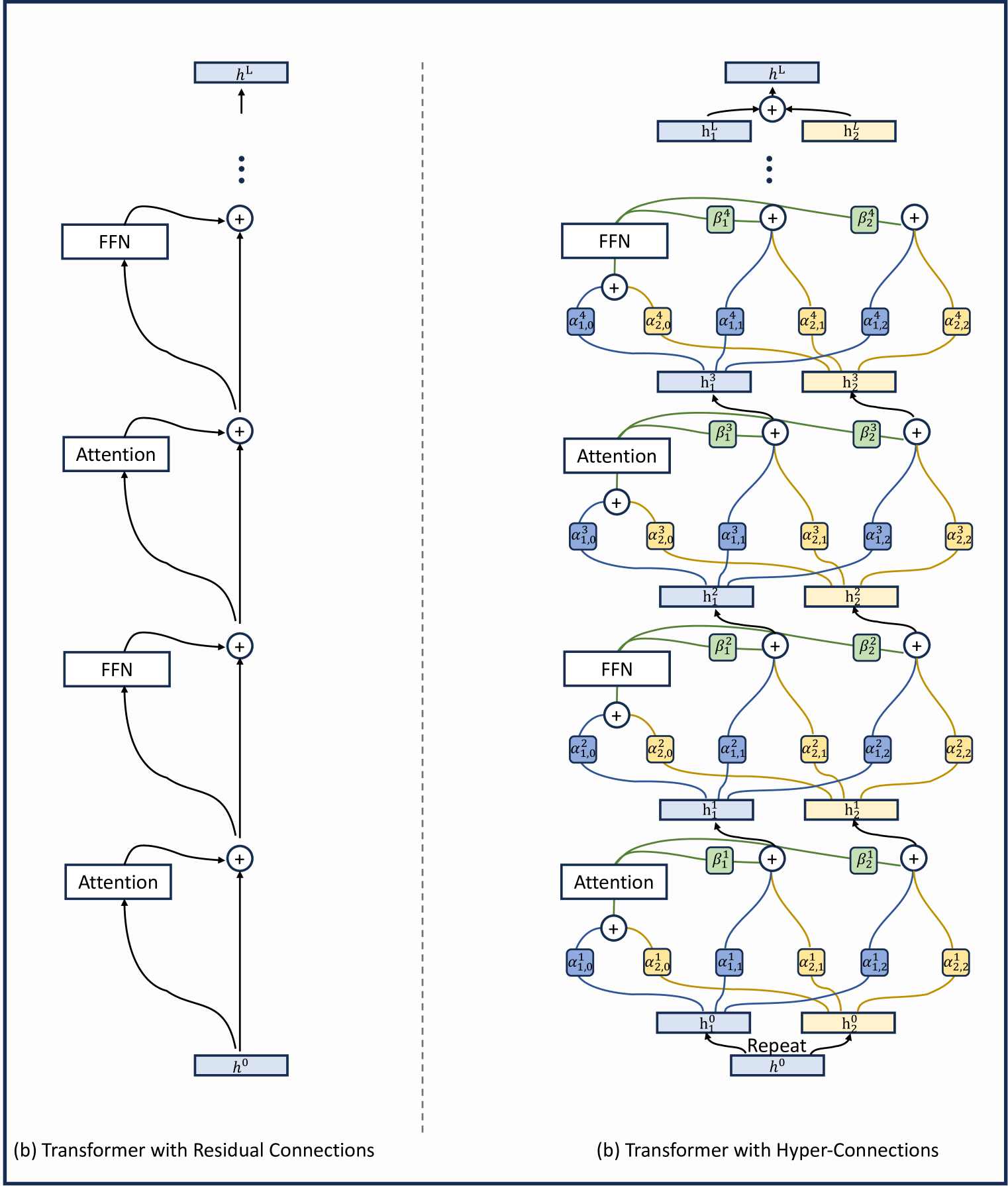
首先，我们对输入的embedding扩展为n份（n称作expansion rate），之后每一层的输入都会是n个hidden vectors，然后在上面构建连接。

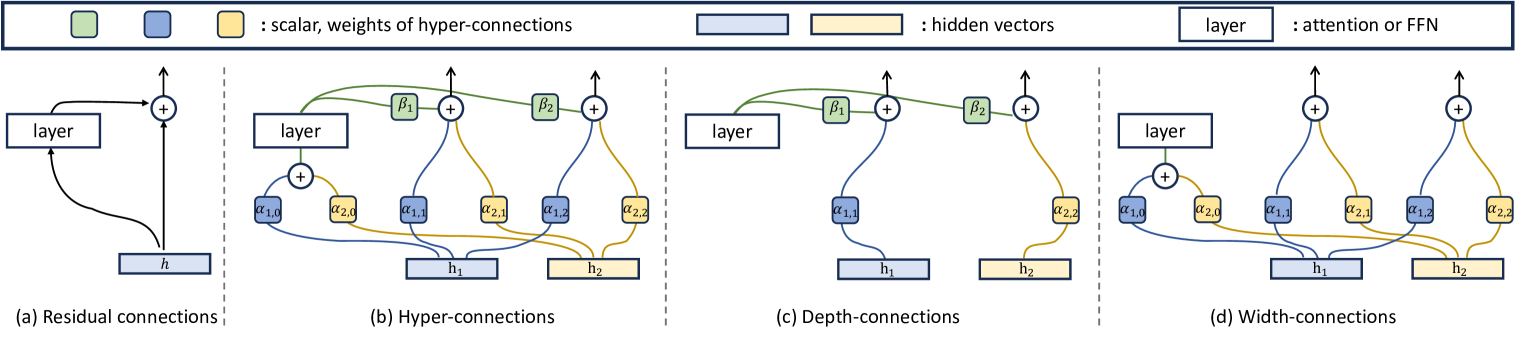
(a)残差连接

(b)Hyper-connections:β₁, β₂, α_0, 0, α_0, 1, α_1, 0, α_1, 1, α_2, 1, 和 α_2, 2是可学习的标量或由网络预测的标量，具体取决于特定的 HC 版本。这些连接实现横向信息交换和跨深度的特征垂直集成。

(c)度连接在层输出和隐藏向量h₁之间进行加权求和。

(d)宽度连接允许隐藏向量h₁和h₂之间的信息交换。

如上图所示，Hyper-Connections会对这些hidden vectors建立以下两类连接：

深度连接（Depth-Connections）：类似于残差连接，但通过为输入与输出之间的连接分配可学习的权重，允许网络灵活调整不同层之间的连接强度。
宽度连接（Width-Connections）：在每一层中实现Hidden Vector之间的信息交互，增强特征融合能力，从而提升模型的表示效果。

2.1.2 静态与动态Hyper-Connections

Hyper-Connections 可以分为静态和动态两种类型：

Static Hyper-Connections (SHC)：连接权重在训练完成后保持固定，不随输入变化。
Dynamic Hyper-Connections (DHC)：连接权重根据输入动态变化，能够自适应不同的输入，通常效果更优。

首先，考虑第k层的输入hidden vectorh^k − 1 ∈ ℝ^d (或h^k − 1 ∈ ℝ^d × 1)。网络的初始输入为h⁰，并将h⁰ ∈ ℝ^d复制n次，形成初始的Hyper Hidden Matrix：

这里，n称为扩展率（Expansion Rate）。在第k层，输入是上一层的Hyper Hidden Matrixh^k − 1 ∈ ℝ^n × d ，即：

对最后一层的 Hyper Hidden Matrix 按行求和，得到最后所需要的所需的hidden vector。为了简化后续分析中的符号表示，我们省略层索引，记 Hyper Hidden Matrix 为：

Hyper-Connections可以用一个矩阵来表示，对于扩展率为n的情况，Hyper-Connections矩阵HC如下：

考虑一层网络𝒯，它可能是Transformer中的attention层或者是FFN层。Hyper-Connections的输出Ĥ可以简单地表示为：

也就是说用A_m作为权重对输入进行加权求和，得到当前层的输入h₀ ：

h₀^⊺ = A_m^⊺H

同时，A_r 用于将H映射为H^′，表示如下：

H^′ = A_r^⊺H

最终的输出表达式为：

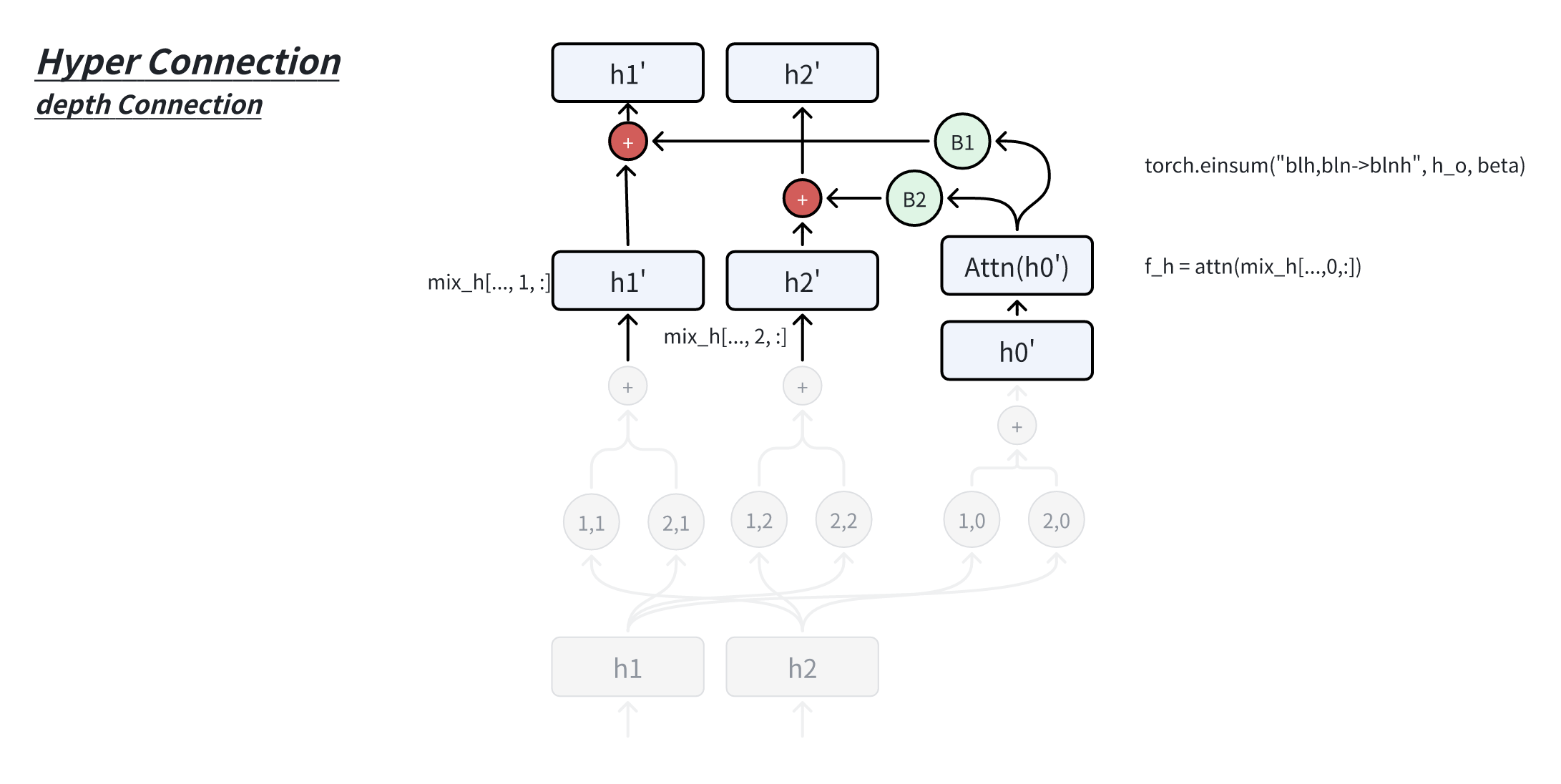
Ĥ = B^⊺(𝒯h₀)^⊺ + H^′

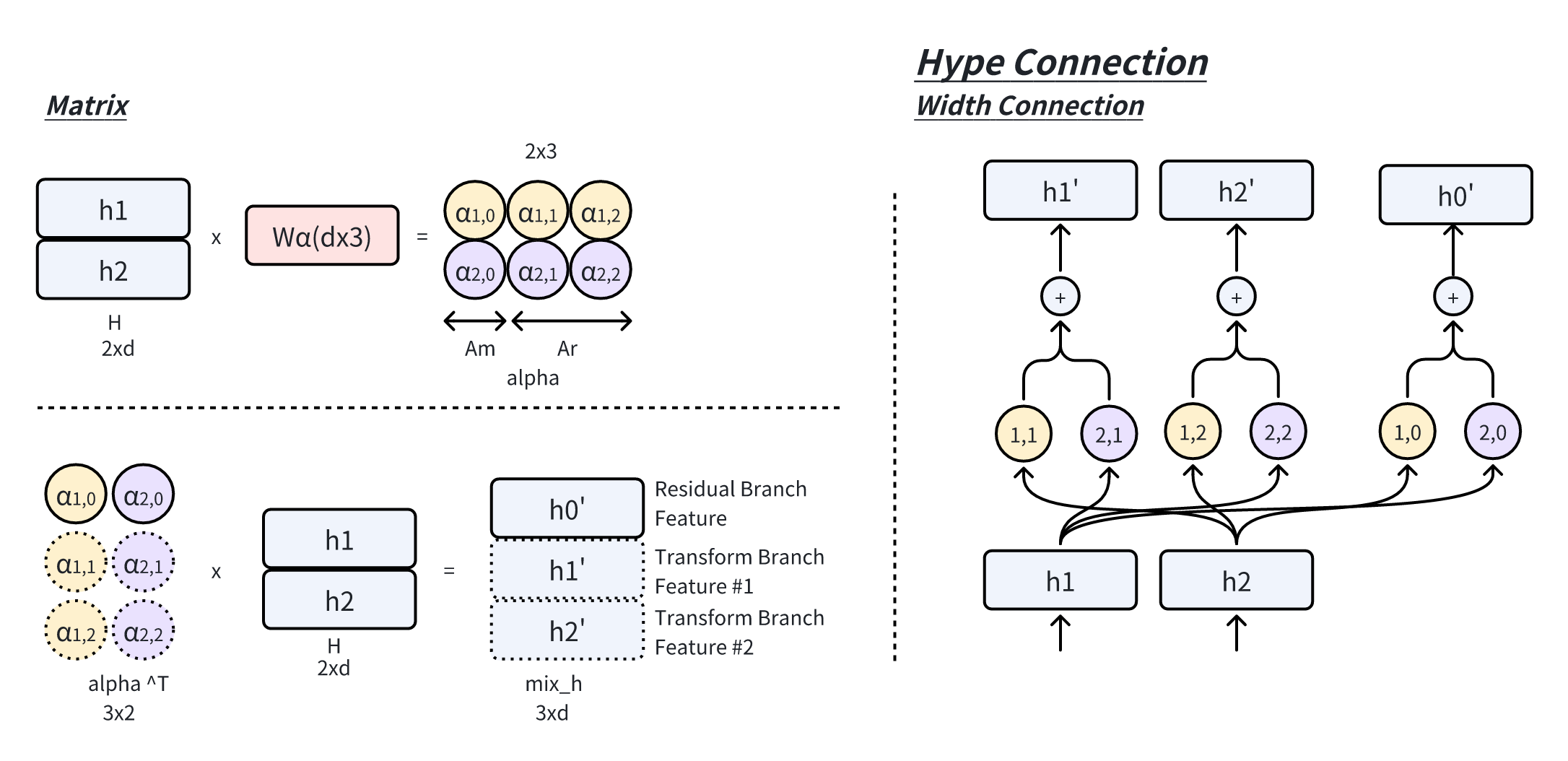
深度连接(depth-connections)可以解耦，如下矩阵所示，如具有n = 2扩展率的HC图中的(a)

当前层的输出权重由第一行B表示，输入权重由最后一行diag(A_r)表示。我们用diag(A_r)表示 A_r对角线元素的扁平化向量。

宽度连接(width-connections)矩阵定义如下，如具有n = 2扩展率的HC图中的(b)

采用超连接的算法在算法伪代码如下:

2.2 Dynamic Hyper-Connections的实现

Hyper-Connections 矩阵ℋ𝒞的元素可以动态依赖于输入H。动态 Hyper-Connections 的矩阵表示如下：

给定层𝒯和输入H，动态 Hyper-Connections 的输出可以表示为：

Ĥ = ℋ𝒞(H)(𝒯, H)

在实际操作中，动态 Hyper-Connections 是结合静态和动态矩阵实现的。动态参数通过线性变换生成。为了稳定训练过程，在线性变换前加入归一化，随后使用 tanh 激活函数，并通过一个可学习的缩放因子进行调整。动态参数的计算公式如下所示：

下图（右）快速求得多个缩放因子

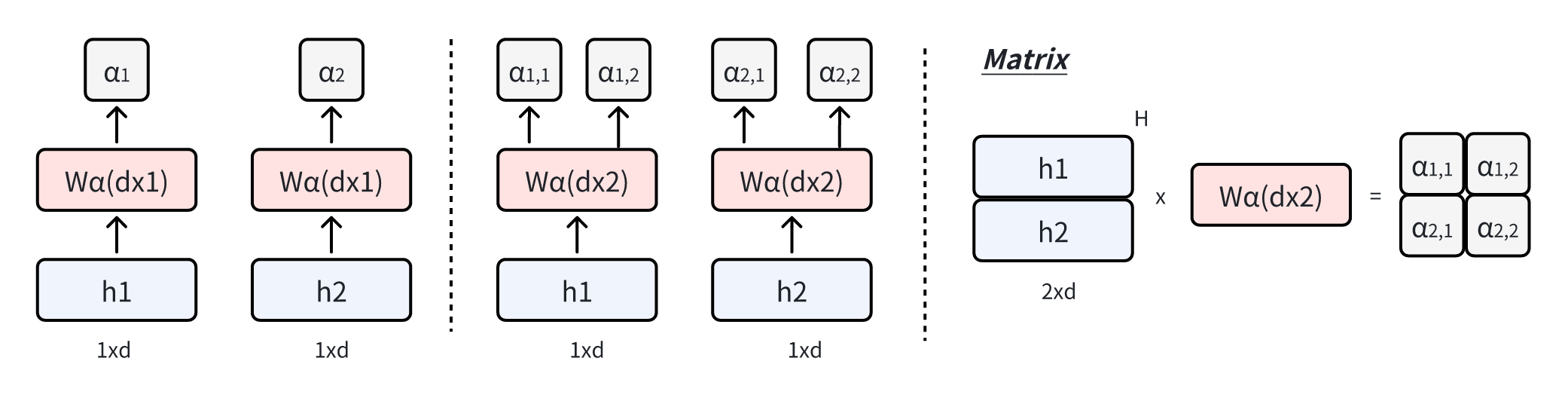
在 HC 论文代码里，对 A_m 和 A_r 的计算进行了算子融合，如W_α ∈ ℝ^{d × n + 1}

实验表明，在语言建模任务中，动态 Hyper-Connections 的效果优于静态 Hyper-Connections。Pytorh代码如下：

# Algorithm 2 Pseudocode of hyper-connections in a PyTorch-like style.
    """
    h: hyper hidden matrix (BxLxNxD)
        B: batch_size
        L: Seq_len
        N: expansion rate
        D: feature dim
    """
# h: hyper hidden matrix (BxLxNxD)
class HyperConnection(nn.Module):
    def __init__(self, dim, rate, layer_id, dynamic, device=None):
        super(HyperConnection, self).__init__()

        self.rate = rate
        self.layer_id = layer_id
        self.dynamic = dynamic

        # 静态偏置量
        ## B
        self.static_beta = nn.Parameter(torch.ones((rate,), device=device))

        # Ar+Am
        init_alpha0 = torch.zeros((rate, 1), device=device)
        init_alpha0[layer_id % rate, 0] = 1.
        self.static_alpha = nn.Parameter(torch.cat([init_alpha0, torch.eye((rate), device=device)], dim=1))

        if self.dynamic:
          # Wmr = cat(Wm, Wr)
            self.dynamic_alpha_fn = nn.Parameter(torch.zeros((dim, rate+1), device=device))
            self.dynamic_alpha_scale = nn.Parameter(torch.ones((1, device=device)) * 0.01)

            # WB
            self.dynamic_beta_fn = nn.Parameter(torch.zeros((dim, ), device=device))
            self.dynamic_beta_scale = nn.Parameter(torch.ones((1, device=device)) * 0.01)
            self.layer_norm = LayerNorm(dim)

    def width_connection(self, h):
        # get alpha and beta
        norm_h = self.layer_norm(h)

        # Note: 求 Am(H) 和 Ar(H)
        if self.dynamic:
            wc_weight = norm_h @ self.dynamic_alpha_fn
            wc_weight = F.tanh(wc_weight)
            dynamic_alpha = wc_weight * self.dynamic_alpha_scale
            alpha = dynamic_alpha + self.static_alpha[None, None, ...]
        else:
            alpha = self.static_alpha[None, None, ...]

        # Note: 求 B(H)
        if self.dynamic:
            dc_weight = norm_h @ self.dynamic_beta_fn
            dc_weight = F.tanh(dc_weight)
            dynamic_beta = dc_weight * self.dynamic_beta_scale
            beta = dynamic_beta + self.static_beta[None, None, ...]
        else:
            beta = self.static_beta[None, None, ...]

        # 缩放因子计算完毕
        # Note: 缩放因子对输入进行缩放
        # alpha 因子是融合了 Am和Ar, mix_h 是包含残差分支和多条变换分支
        mix_h = alpha.transpose(-1, -2) @ h
        # mix_h[...,0,:] 残差分支
        # mix_h[...,1:,:] 变换分支
        return mix_h, beta

    def depth_connection(self, self, mix_h, h_o, beta):
        # Note: beta 缩放因子处理残差分支, 再与变换分支 `mix_h` 进行相加
        h = torch.einsum("blh,bln->blnh", h_o, beta) + mix_h[..., 1:, :]
        return h

# Algorithm 3 Pseudocode of transformer with hyper-connections in a PyTorch-like style.
# h: hyper hidden matrix (BxLxNxD)
# attn_hyper_connection, ffn_hyper_connection: hyper-connection modules
# attn_norm, ffn_norm: normalization modules

# Attention Block
# 计算缩放因子, 缩放特征 mix_h
mix_h, beta = attn_hyper_connection.width_connection(h)
h = attn_norm(mix_h[..., 0, :])
# 对缩放后的残差特征进行建模
h = self.attention(h)
# 获取最后的特征
h = attn_hyper_connection.depth_connection(mix_h, dropout(h), beta) # 分解 f_h*beta + mix_h[...,1:,:]

# FFN Block
mix_h, beta = ffn_hyper_connection.width_connection(h)
h = ffn_norm(mix_h[..., 0, :])
h = ffn(h)
h = ffn_hyper_connection.depth_connection(mix_h, dropout(h), beta)

2.3 初始化

为了使超连接的初始化与预规范残差连接等效，我们采用以下初始化策略。在公式 6、7 和 8 中的动态参数W_β, W_m, 和W_r被初始化为 0，而静态矩阵初始化如下：

其中k是层的索引，mod表示取模运算。

三、Hyper-Connections的一些insights

Paper中讨论到，Pre-Norm 和 Post-Norm 可以被看作是 Hyper-Connections 的特例，其中两者的连接形式实际上是不可训练的。对此，我们进一步引入了 SEQUENTIAL-PARALLEL DUALITY（顺序-并行二象性）的概念，说明了 Hyper-Connections 如何通过动态调整网络层的排列方式（顺序或并行），从而优化网络的性能。这样的设计使得模型不仅能够灵活地组合传统的层排列方式，还可以通过动态学习形成更高效的混合排列结构，突破了固定连接模式的限制。

3.1 残差连接作为不可训练的超连接

Pre-Norm和Post-Norm可以表示为以下扩展率为n = 1的Hyper-Connections矩阵：

其中，σ_i 和 σ_o分别表示神经网络层输入和输出的标准差，σ_io 表示它们之间的协方差。

对于 Pre-Norm，其 Hyper-Connections 矩阵是一个2 × 2的矩阵，右下三角部分填充为1，其余部分为占位符0。

对于 Post-Norm，权重依赖于输入和输出的方差及协方差，形成一个2 × 2的矩阵。因此，这两种方法的 Hyper-Connections 矩阵均为不可学习的。

相比之下，本工作提出的方法使用了一个(n + 1) × (n + 1)的 Hyper-Connections 矩阵，其权重是可学习的，并且可以根据输入动态预测。

3.2 串行-并行对偶性

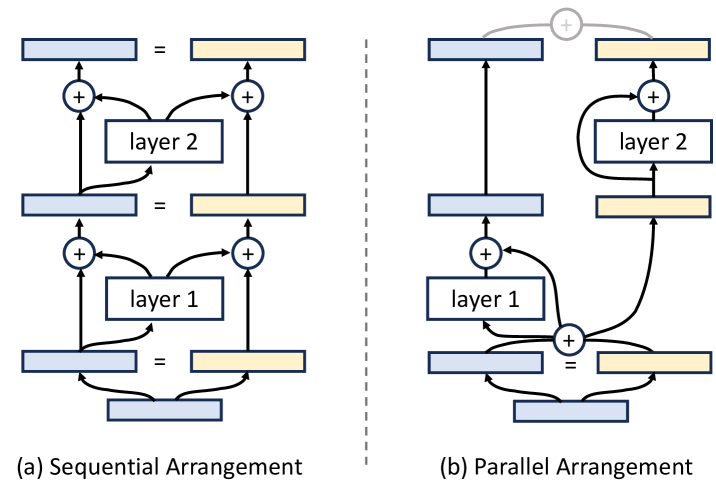
对于一组神经网络层，可以选择将它们顺序排列或并行排列。而通过引入 Hyper-Connections，模型能够学习如何动态地重新排列这些层，形成顺序配置与并行配置的混合结构。

论文讨论了扩展率设置为n = 2的情况。如果 Hyper-Connections 的矩阵形式如下所示，则网络层将被顺序排列：

在这种情况下，深度连接退化为残差连接，如上图(a)所示。

当奇数层和偶数层的Hyper-Connections矩阵分别定义为以下形式时，神经网络每两层将被并行排列，类似于 Transformer 中的parallel transformer block的排列方式，如上图(b) 所示。

因此，通过学习不同形式的Hyper-Connections矩阵，网络层的排列可以超越传统的顺序和并行配置，形成软混合甚至动态排列。对于静态Hyper-Connections，网络中的层排列在训练后保持固定；而对于动态Hyper-Connections，排列可以根据每个输入动态调整。

四、实验结果

4.1 1B dense 模型实验

实验主要集中在LLMs的预训练上，涵盖了dense模型和MoE模型。

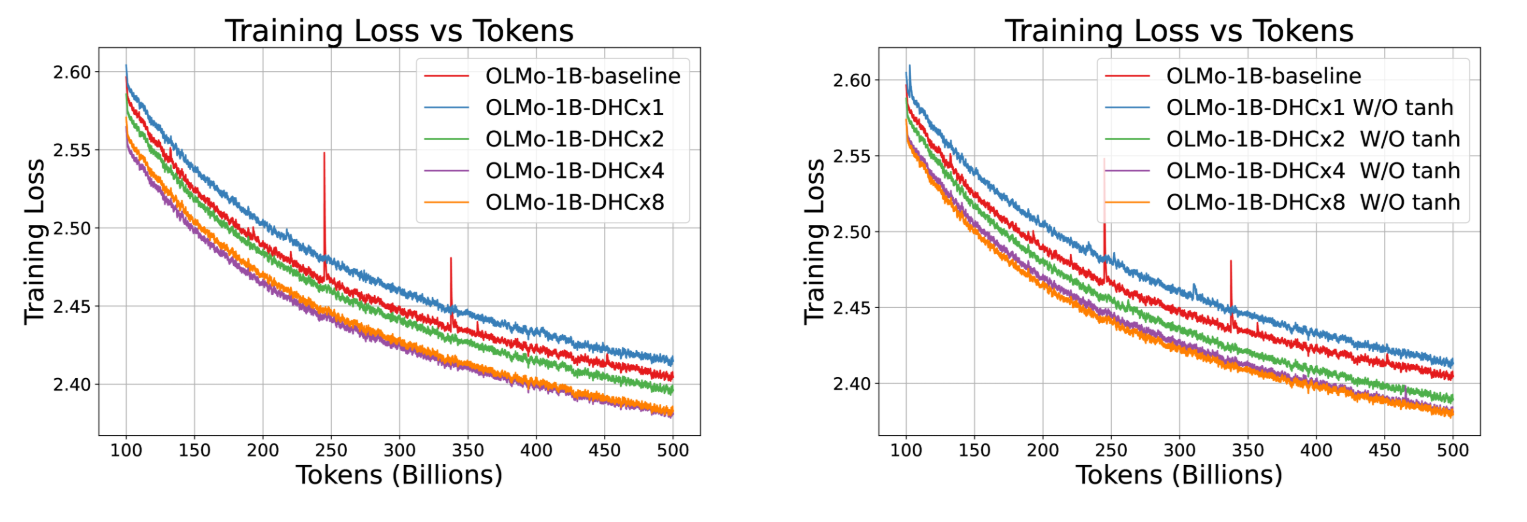
不同扩展率下训练损失曲线的比较。左子图包括在不同扩展率下具有动态超连接（DHC）的模型，而右子图显示了省略 tanh 函数的影响。两个子图都说明了如何通过增加扩展率来提高 500B token 的训练损失性能。结果使用系数为 0.99 的指数移动平均进行平滑处理。

当扩展率大于 1 时，模型性能显著提升，训练过程更加稳定，同时有效消除了训练中 loss 的波动现象（spikes）。

4.2 7B dense 模型实验

我们scale到了7B 模型，效果也十分亮眼，同样的，可以看到有hyper-connections的网络训练更稳定。

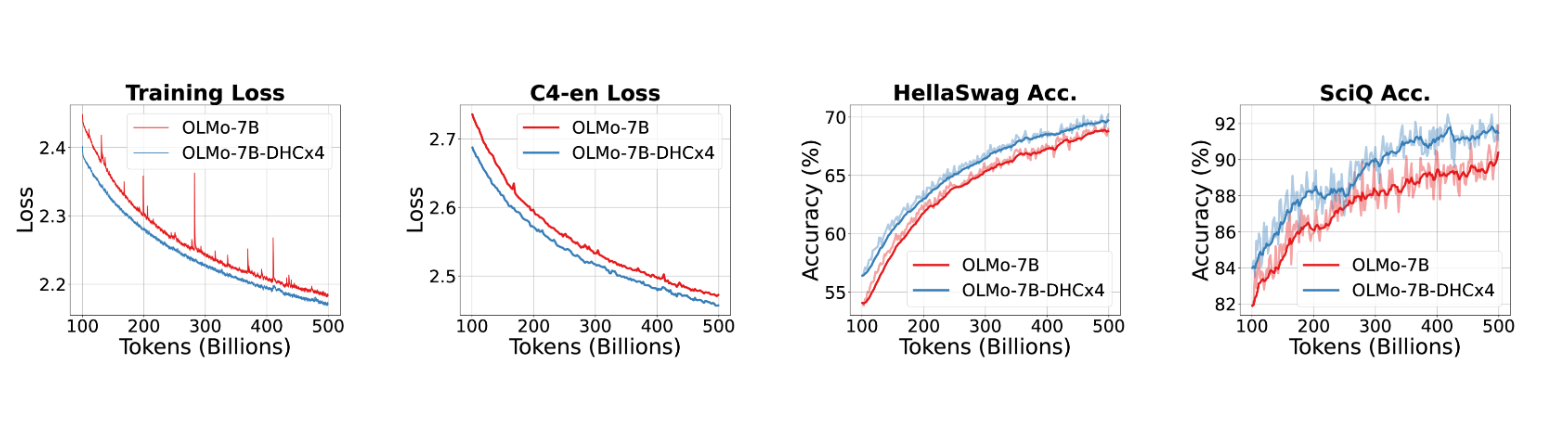
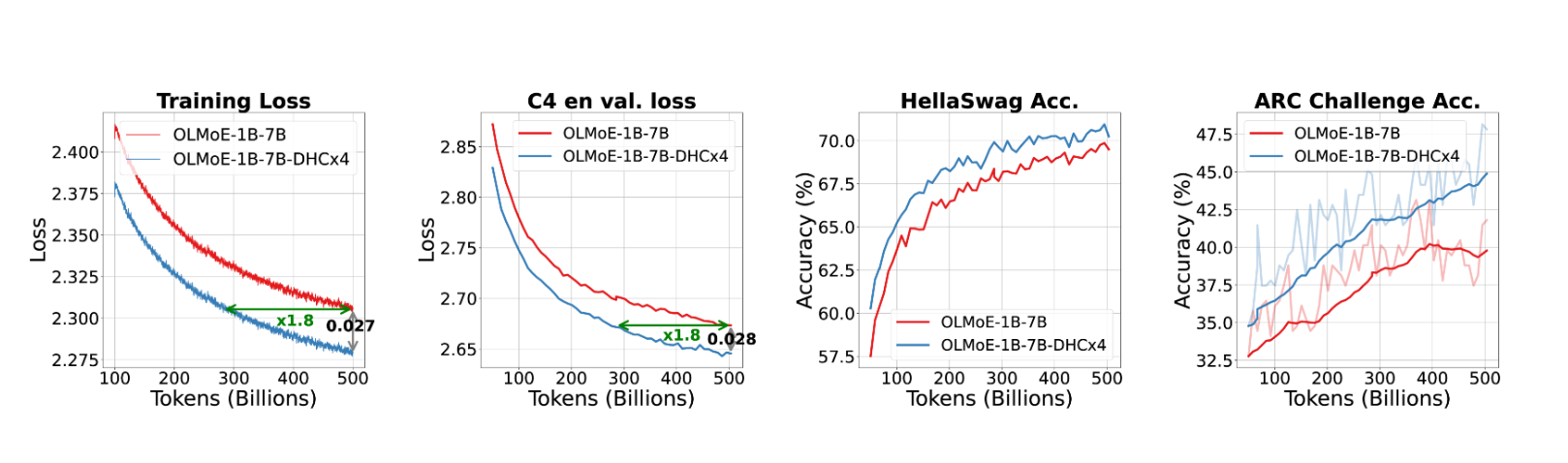
和 (2) OLMo-7B 和 OLMo-7B-DHC×4 模型的训练损失（0.99 EMA 平滑）和 C4-en 验证损失。(3) 和 (4) 在 hellaswag 和 sciq 上的准确率曲线，展示了 OLMo-7B-DHC×4 模型的优越性能。

4.3 7B候选激活1.3B的 MoE模型实验

在 OLMoE 评估设置下使用 500B tokens 训练 MoE 模型的下游评估结果。ARC-C 代表 ARC-Challenge，ARC-E 代表 ARC-Easy。MMLU Var 是 MMLU 的修改版本，包含变化的少样本示例，在早期训练中提供稳定反馈，如 OLMoE 设置所述。

下游指标基本上全都涨，在ARC-Challenge上甚至涨了6个点。

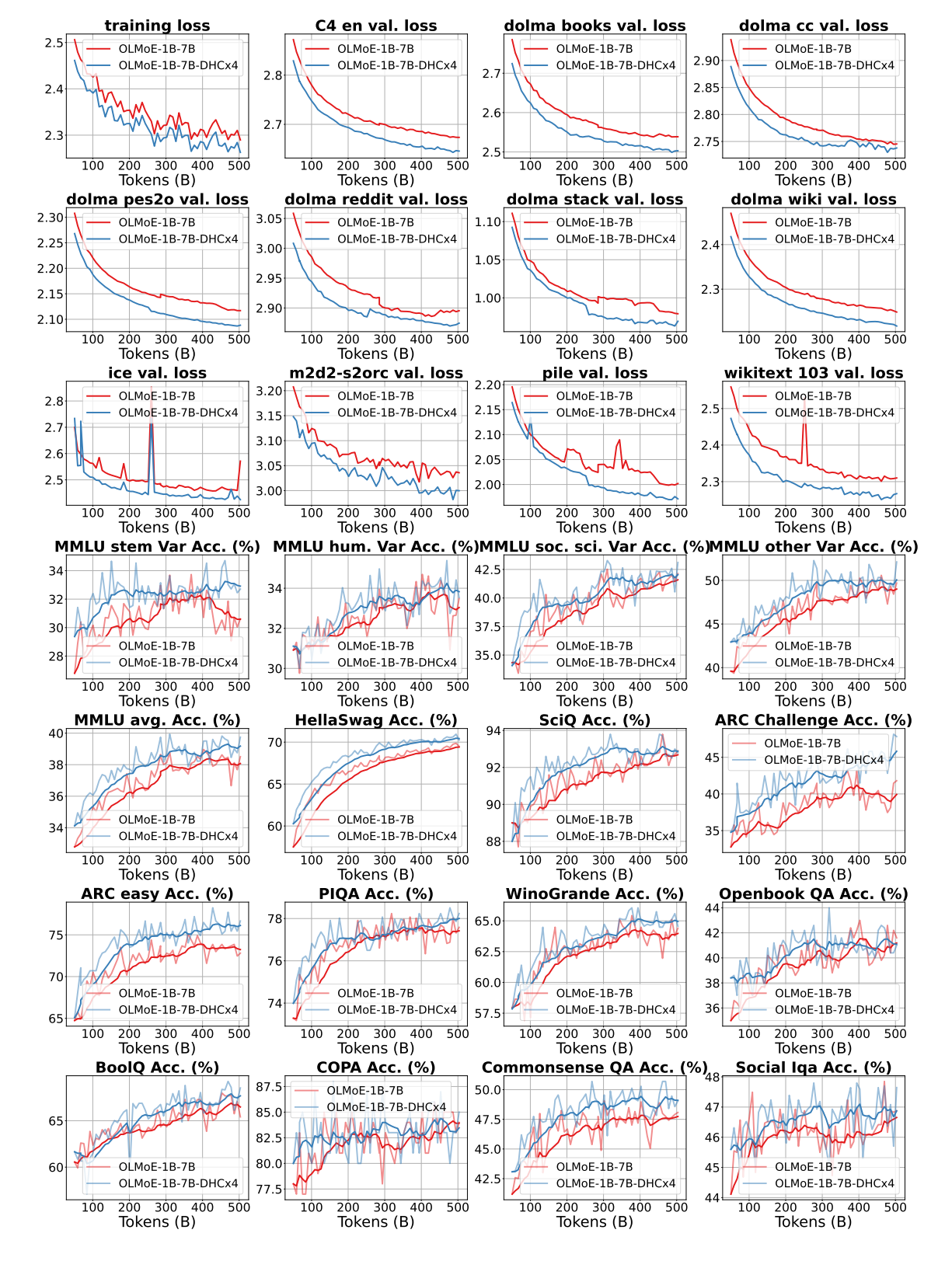
OLMoE-1B7B 和 OLMoE-1B7B-DHC×4模型在 V3 验证集上的损失曲线以及下游任务上的准确率曲线。

4.4 可视化分析

我们对Hyper-Connections进行展开，所谓展开就是计算每一层的Hidden Vector 对后面所有层的Hidden Vectors的影响权重。我们发现非常有趣的现象：

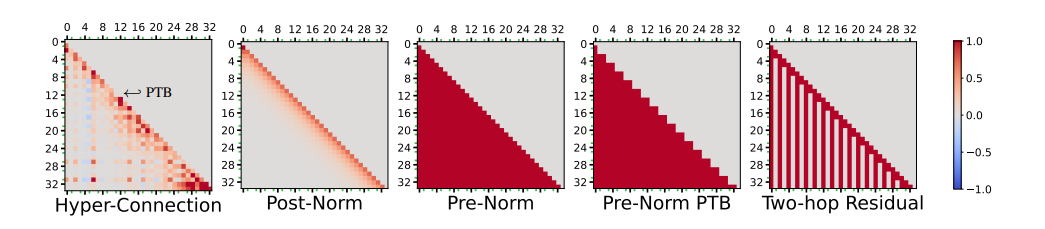
超连接和各种相关基线方法的连接矩阵的可视化。具有奇数 id 的注意力层用绿色对勾标记。

连接模式的对比

Hyper-Connections 显示出一种大致 Λ形连接模式，即每层输出对邻近层的贡献较大，同时浅层对远层有长期贡献。这种模式融合了 Pre-Norm 和 Post-Norm 结构的特性。
Pre-Norm 基线 的连接矩阵呈下三角形，反映了每层仅与前一层直接相连。
Post-Norm 基线 的连接仅限于相邻层，权重随着深度迅速衰减。
two-hop残差连接 的连接模式表现为仅隔层有贡献，形成条状分布。

输入词嵌入的影响

在 Hyper-Connections 的连接矩阵中，输入词嵌入对大部分层有显著贡献，但对最终输出的影响较小。这表明过多依赖输入词嵌入可能对预测下一词产生负面影响。

并行 Transformer 模式

Hyper-Connections 能局部学出来并行 Transformer block。即，attention和FFN并行，这在连接矩阵中表现为局部的锯齿状模式。

注意力层的长期连接

注意力层的输出在连接矩阵中更倾向于长期贡献，特别是对底层（如词嵌入层）的依赖更强。这种模式类似于two-hop 残差连接设计。

五、总结

本文介绍了Hyper-Connections，它是针对残差连接在梯度消失和表示崩溃之间的跷跷板现象而设计的。Hyper-Connections在LLMs Pretrain以及视觉任务中都表现出显著的性能提升。值得注意的是，Hyper-Connections的引入几乎不增加额外的计算开销或参数量，因此它可能具有广泛的应用潜力。它的问题在于会增加显存，需要做算子级别的重计算，减少显存的占用。

Reference

LLM

#HC

Hyper-Connections

https://mztchaoqun.com.cn/posts/D106_Hyper-Connections/

作者

mztchaoqun

发布于

2026年1月23日

许可协议

Sinkhorn-Knopp算法上一篇

语言模型训练与推理：从概念到代码下一篇