理解 PPO 和 GRPO
一、简介
在强化学习(RL)中,仅仅知道“你得分多少”往往是不够的。单纯追求高分可能导致各种副作用,如过度探索、模型不稳定,甚至偏离合理策略的“走捷径”行为。为了应对这些挑战,RL 引入了多种机制,如评价者(价值函数)、裁剪操作、参考模型,以及较新的群体相对策略优化(GRPO)。
为了让这些概念更直观,让我们打个比方:把 RL 训练过程比作小学考试场景。我们(被训练的模型)就像努力取得高分的同学,评分的老师就像奖励模型,而父母根据我们的成绩发零花钱则类似于评论家。接下来,让我们一步步解释为什么仅凭最终分数是不够的,评论家、裁剪和参考模型如何发挥作用,以及 GRPO 如何扩展这些理念。
二、仅使用奖励的朴素方法:问题是什么?
假设我和弟弟在同一个小学班级。老师评分我们的考试,给出“绝对分数”。我通常在 100 分中得 80 分以上,而弟弟经常得 30 分左右。然后我们直接拿着这些分数去找爸爸要零花钱——也就是说我们的“奖励”(在 RL 术语中)就是原始考试分数。谁得分高就得到更多零花钱。
乍一看,这似乎没什么问题。但很快就会出现两个大问题:
- 不公平:如果我的哥哥通过大量努力从 30 分提高到 60 分,他仍然远不如我通常的 80 多分。他得不到他应得的鼓励。
- 不稳定性:我自己追求更高分数可能会导致极端的学习方法(例如,全天候熬夜学习,通宵达旦)。有时我可能考 95 分,有时只有 60 分,所以我的分数——以及相应的奖励信号——波动极大。
结果,使用绝对分数作为奖励会导致大幅度的奖励波动,而我的哥哥最终会觉得一点点的进步不值得去尝试。
2.1 数学对应关系
在强化学习中,如果我们简单地进行:
𝒥naive(θ) = 𝔼(q, o) ∼ (data, πθ)[r(o)],
这意味着“仅优化最终奖励”,我们可能会遇到高方差和部分改进激励不足的问题。换句话说,Actor 缺乏与其当前水平相匹配的基线,这阻碍了训练效率。
三、引入评价者:使用“预测分数线”来改进奖励
认识到这个问题,Dad 意识到“这不仅仅是关于绝对分数;关键在于你相对于当前水平的改进程度。”
所以他的决定是:
- 将我的“预测分数线”设为 80 分,我弟弟的设为 40 分。如果我们考试超过这些分数线,就能得到更多的零花钱;如果没达到,就只有很少或者没有。
因此,如果我弟弟努力学习,从 30 分提升到 60 分,他就比自己的“预测分数线”高出 20 分,这意味着能获得丰厚的奖励。而如果我保持在 80 分左右,增量收益较小,所以我未必能比他多得很多。这种安排鼓励每个人从自己的基准点出发提升,而不是单纯比较绝对分数。
当然,爸爸很忙,所以一旦设定了分数线,它并不会一成不变——他需要随着我们的进步不断“调整”。如果我弟弟提升到 60 分左右,那么 40 分的基准线就不再公平。同样地,如果我持续在 85 分左右徘徊,爸爸可能也需要调整我的分数线。换句话说,爸爸也必须学习,具体是关于我和弟弟进步的速度。
3.1 数学对应关系
在强化学习中,这条“得分线”被称为值函数,Vψ(s)。它充当基准。我们的训练目标从“仅仅是奖励”演变为“我们超越基准的程度”,用优势函数表示:
At = rt − Vψ(st).
对于给定的状态st和动作ot,如果实际奖励超过评论家的预期,这意味着该动作表现优于预期。如果较低,则该动作表现不佳。在最简单的公式中,我们优化类似:
𝒥adv(θ) = 𝔼[A(o)], where A(o) = r(o) − Vψ(o).
通过减去这条“得分线”,我们减少了训练中的方差,给超出预期的动作提供更高的梯度信号,并惩罚表现不足的动作。
四、添加裁剪和最小值操作:防止过度更新
即使有“得分线”,新问题也可能出现。例如:
- 如果我突然在测试中取得突破,得分达到 95 或 100,爸爸可能会给我一个巨大的奖励,推动我在下次考试前采取过于激进的学习模式。我的成绩可能会在极端值之间波动(95 和 60),导致巨大的奖励波动。
因此,爸爸决定控制我每一步更新学习策略的幅度——他不会因为一次好成绩就给我指数级增加零花钱。如果给太多,我可能会走向极端探索;如果给太少,我可能没有动力。所以他必须找到平衡。
4.1 数学对应关系
在 PPO(近端策略优化)中,这种平衡是通过“裁剪”机制实现的。PPO 目标的核心包括:
min (rt(θ)At, clip(rt(θ), 1 − ε, 1 + ε) At),
其中
表示该动作在新旧策略之间的概率比。如果该比率偏离 1 太远,它会被限制在[1 − ε, 1 + ε]内,这限制了策略在一次更新中可以改变的幅度。
换句话说:
- 得满分可以获得额外奖励,但爸爸会设一个“上限”,以免我过分。他会在下次考试时重新评估,保持稳定的方法,而不是助长极端波动。
五、参考模型:防止作弊和极端策略
即便如此,如果我只专注于高分,我可能会采取一些可疑的手段——比如作弊或恐吓老师给我满分。显然,这违反了所有规则。在大语言模型的领域里,一个类似的情况是生成有害或虚假的内容来人为地提高某些奖励指标。
爸爸因此设定了一条额外的规则:
- “无论怎样,你都不能太偏离你最初诚实的学习方法。如果你偏离基准太远,即使得分很高,我也会取消你的资格并扣留你的零花钱。”
5.1 数学对应关系
在 PPO 中,这通过向参考模型(初始策略)添加 KL 惩罚来体现。具体来说,我们包含类似这样的内容:
−β 𝔻KL(πθ ∥ πref)
在损失中。这可以防止 Actor 偏离原始的、合理的策略太远,避免“作弊”或其他超出界限的行为。
六、GRPO:用“多个模拟平均值”替代价值函数
有一天,爸爸说:“我没有时间不断评估你的学习进度和画新的分数线。为什么不先做五套模拟测试,然后把它们的平均分作为你的预期分数呢?如果你在真实测试中超过这个平均分,那就说明你比自己的预期做得更好,我会奖励你。否则,你不会得到太多。”我和哥哥,还有可能更多的同学,可以各自依赖一套个人模拟测试,而不是一个爸爸需要不断调整的外部“价值网络”。
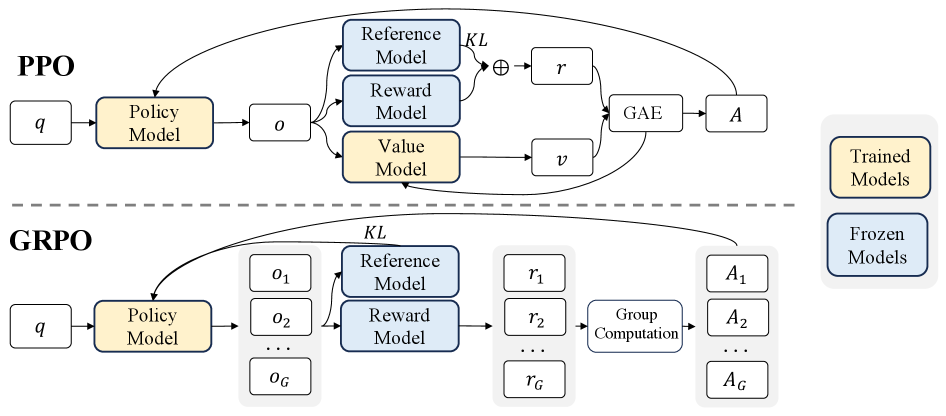
到目前为止,我们看到 PPO 依赖于 Actor + Critic + Clip + KL 惩罚框架。然而,在大语言模型(LLM)场景中,Critic(价值函数)往往需要和 Actor 一样大才能准确评估状态,这可能会很昂贵,有时甚至不切实际——特别是如果你只有一个最终奖励(比如最终答案质量)在最后。
因此,组相对策略优化(GRPO)登场了。其核心思想是:
- 没有为评价者设置单独的价值网络,
- 对同一问题或状态,从旧策略中采样多个输出,
- 将这些输出的平均奖励视为基线,
- 高于平均值的产生“正向优势”,低于平均值的产生“负向优势。”
与此同时,GRPO 保留了 PPO 的 Clip 和 KL 机制,以确保稳定、合规的更新。
6.1 数学对应关系
根据 DeepSeekMath 的技术报告,GRPO 目标函数(省略部分符号)为:
其中
通过平均同一问题的多个输出并归一化来计算一个“相对分数”。这样,我们不再需要一个专门的价值函数,但仍然能获得一个动态的“分数线”,从而简化训练并节省资源。
七、结论:反思与未来展望
用小学考试作类比,我们一步步从原始绝对分数过渡到 PPO 的完整机制(评价者、优势函数、裁剪、参考模型),最终到 GRPO(利用多个输出的平均分数来消除价值函数)。以下是一些关键要点:
- 评价者的作用:为每个状态提供“合理的预期”,显著降低训练方差。
- 裁剪与最小值机制:限制更新幅度,防止对单个“突破性”考试过度反应。
- 参考模型:阻止“作弊”或极端偏离,确保策略与其初始状态保持合理的一致性。
- GRPO 的优势:在大语言模型中,它消除了对单独值网络的需求,减少内存和计算成本,同时与“比较式”奖励模型设计高度契合。
就像爸爸那样,让孩子们自己模拟多次考试,然后将他们的平均分作为基准,GRPO 在避免维护一个庞大的 Critic 的同时,仍然提供相对的奖励信号。它保留了 PPO 的稳定性和合规性特征,但简化了流程。