梯度提升树GBDT

1.提升树

提升树模型实际采用加法模型（即基函数的线性组合）与前向分步算法，以决策树为基函数的提升方法称为提升树（Boosting Tree）。提升树模型可以表示为决策树的加法模型：

其中， T(x; Θ_m) 表示决策树； Θ_m 为决策树的参数； M 为树的个数。

1.1提升树算法

提升树算法采用前向分步算法。首先确定初始提升树 f₀(x) = 0 ,第 m 步的模型是：

f_m(x) = f_m − 1(x) + T(x; Θ_m)

其中， f_m − 1(x) 为当前模型，通过经验风险极小化确定下一棵决策树的参数 Θ_m

由于树的线性组合可以很好的拟合训练数据，即使数据中的输入和输出之间的关系很复杂也是如此，所以提升树是一个高功能的学习算法。

对于二分类问题，提升树算法只需将AdaBoost算法中的基本分类器限定为二分类树即可 。这里不再讨论，下边主要讨论回归问题的提升树。

已知训练集T = {(x₁, y₁), (x₂, y₂), ⋯, (x_N, y_N)}, x_i ∈ 𝒳 ⊆ Rⁿ , 𝒳 为输入空间， y ∈ 𝒴 ⊆ R , 𝒴 为输出空间。将输入空间 𝒳 划分为 J 个互不相交的区域 R₁, R₂, ⋯, R_J ，并且每个区域上确定输出的常量 c_j ,那么树可表示为

其中，参数 Θ = {(R₁, c₁), (R₂, c₂), ⋯, (R_J, c_J)} 表示树的区域划分和各区域上的常数。 J 是回归树的复杂度即叶节点个数。

回归问题提升树使用以下前向分步算法：

在前向分步算法的第 m 步，给定当前模型 f_m − 1(x) ,需求解

得到 Θ̂_m ，即第 m 棵树的参数。当采用平方误差损失函数时， L(y, f(x)) = (y − f(x))² ,即：

这里， r = y − f_m − 1(x) 是当前模型拟合数据的残差(residual).所以，对于回归问题的提升树算法来说，只需简单地拟合当前模型的残差。

只看算法本身很难理解为什么直接拟合残差就可以，引用别人博客的例子来加强理解：每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。

1.2提升树算法流程

输入：训练数据T = {(x₁, y₁), (x₂, y₂), ⋯, (x_N, y_N)}, x_i ∈ 𝒳 ⊆ Rⁿ , y ∈ 𝒴 ⊆ R ;

输出：提升树 f_M(x) .

(1)初始化 f₀(x) = 0

(2)对 m = 1, 2, ⋯, M

(a)计算残差 r_mi = y_i − f_m − 1(x_i), i = 1, 2, ⋯, N

(b)拟合残差 r_mi 学习一个回归树，得到 T(x; Θ_m)

(c)更新 f_m(x) = f_m − 1(x) + T(x; Θ_m)

(3)得到回归问题的提升树

1.3例子

训练数据见下表， x 的取值范围 [0.5, 10.5], y 的取值范围 [5.0, 10.0] ，学习这个回归问题的最小二叉回归树。

求训练数据的切分点，根据所给数据，考虑如下切分点：

1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.5

对各个切分点，求出对应的 R₁, R₂, c₁, c₂ 及

m(s) = min_j, s[min_c1∑_{xi ∈ R1(j, s)}(y_i − c₁)² + min_c2∑_{xi ∈ R2(j, s)}(y_i − c₂)²]

当 s = 1.5 时，R₁ = {1}, R₁ = {2, 3, ⋯, 10}, c₁ = 5.56, c₂ = 7.50, m(s) = 0 + 15.72 = 15.72

s 及 m(s) 的计算结果如下表：

由上表可知，当 x = 6.5 的时候达到最小值，此时R₁ = {1, 2, ⋯, 6},R₁ = {7, 8, 9, 10}, c₁ = 6.24 , c₂ = 8.9 ,所以回归树 T₁(x) 为：

f₁(x) = T₁(x)

用 f₁(x) 拟合训练数据的残差如下表，表中 r_2i = y_i − f₁(x_i)

用 f₁(x) 拟合训练数据的平方误差：

第二步求 T₂(x) .方法与求 T₁(x) 一样，只是拟合的数据是是第一步中得到的残差表，可以得到：

用 f₂(x) 拟合训练数据的平方损失误差：

继续求得：

用 f₆(x) 拟合训练数据的平方损失误差：

假设此时已满足误差要求，那么 f(x) = f₆(x) 即为所求提升树。

2.梯度提升

当提升树的损失函数是平方损失和指数损失函数时，每一步优化是比较简单的，但对于一般损失函数而言，往往每一步优化比较困难。针对该问题，Freidman提出了梯度提升算法。这是利用最速下降法的近似方法，利用损失函数的负梯度在当前模型的值

作为回归问题提升树算法中的残差的近似值，拟合一个回归树。

梯度提升树算法流程

输入：训练数据T = {(x₁, y₁), (x₂, y₂), ⋯, (x_N, y_N)}, x_i ∈ 𝒳 ⊆ Rⁿ , y ∈ 𝒴 ⊆ R ;损失函数 L(y, f(x))

输出：回归树 f̂(x) .

(1)初始化

(2)对 m = 1, 2, ⋯, M

(a)对 i = 1, 2, ⋯, N ，计算

(b)对 r_mi 拟合一个回归树，得到第 m 棵树的叶节点区域 R_mj, j = 1, 2, ⋯, J

(c)对 j = 1, 2, ⋯, J ，计算

c_mj = arg min_c∑_{xi ∈ Rmj}L(y_i, f_m − 1(x_i) + c)

利用线性搜索估计叶结点区域的值，使损失函数极小化；

(d)更新

(3)得到回归树

Shrinkage

Shrinkage的思想认为，每次走一小步逐渐逼近结果，要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树，它认为每棵树只学到了真理的一小部分，累加的时候只累加一小部分，通过多学几棵树弥补不足。

Shrinkage树的更新方式 ,Shrinkage仍然以残差作为学习目标，但对于残差学习的结果，只累加一小部分， v 一般取值0.001-0.01，使得各个树的残差是渐变而不是陡变的，即将大步切成了小步。

3.XGBoost

xgboost(eXtreme Gradient Boosting)是提升树模型，它与决策树是息息相关，它通过将很多的决策树集成起来，从而得到一个很强的分类器，xgboost中主要的思想与CART回归树类似.

3.1 原理

3.1.1 树的复杂度

对数据集D = {(x_i, y_i)}, (∥D∥ = n, x_i ∈ ℝ^m, y_i ∈ ℝ),假设有 K 棵树，则模型为：

其中 ℱ 把树拆分成结构部分 q 和叶子权重部分 w ,结构函数 q 把输入映射到叶子的索引号上面去，而 w 给定了每个索引号对应的叶子分数是什么.

ℱ = {f_t(x) = w_q(x)}, w ∈ R^T, q : R^d → {1, 2, ⋯, T}

如下图：

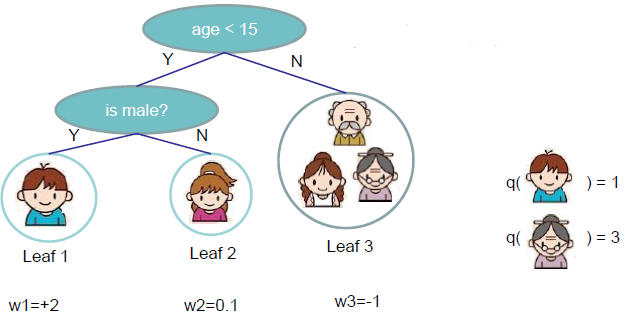
树的复杂度函数: ,其中 T 为叶节点个数， 为 L2 正则化项，也可以用 L1 正则化项 | w_j |.则上图中树的复杂为 .

定义树的结构和复杂度的原因很简单，这样就可以衡量模型的复杂度，从而可以有效控制过拟合。

3.1.2 boosting tree模型

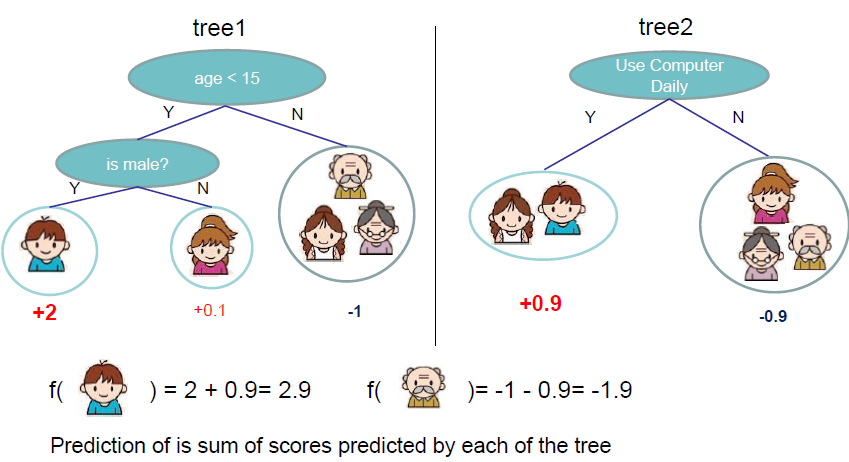
和传统的boosting tree模型一样，xgboost的提升模型也是采用的残差（或梯度负方向(牛顿法)），不同的是分裂结点选取的时候不一定是最小平方损失。 正则化的目标函数：

3.1.3 目标函数的设计

由于 ŷ_i^(t) = ŷ_i^{(t − 1)} + f_t(x_i) ，则目标函数可改写成：

泰勒展开: f(x + Δx) ≃ f(x) + f^′(x)Δx + f^″(x)Δx

并定义:gi = ∂ŷi(t − 1)l(yi, ŷi(t − 1)), hi = ∂ŷi(t − 1)2l(yi, ŷi(t − 1)).

对目标函数使用泰勒展开并简化：

最终的目标函数只依赖于每个数据点的在误差函数上的一阶导数和二阶导数。去除常数项，并定义了分裂候选集合 I_j = {i|q(x_i) = j}，可以进一步改目标函数.

其中 ,对 w_j 求导等于0，可求得：

把 w_j^* 代入目标函数可得：

3.1.4 结构的打分函数

上一节中的Obj代表了当我们指定一个树的结构的时候，我们在目标上面最多减少多少。我们可以把它叫做结构分数(structure score)。如图：

对于每一次尝试去对已有的叶子加入一个分割，计算分割前后的分数差：

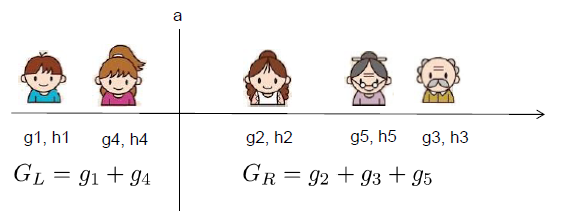
其中 为分割后左子树得分， 为分割后右子树得分， 为不进行分割时的得分， γ 为加入新叶子节点引入的复杂度代价。当 Gain 的值越大时，目标函数值就越小。因此选择 Gain 值最大的节点进行分割。

基于这个分裂的评分函数，我们还可以用来处理缺失值。处理的方法就是，我们把缺失值部分额外取出来，分别放到 I_L 和 I_R 两边分别计算两个评分，看看放到那边的效果较好，则将缺失值放到哪部分。

3.1.4 树节点分裂方法

(1)暴力枚举，显然效率低下。

(2)近似方法

对于每个特征，只考察分位点，减少计算复杂度;学习每棵树前，提出候选切分点;每次分裂前，重新提出候选切分点。XGBoost不是简单地按照样本个数进行分位，而是以二阶导数值作为权重,如下图:

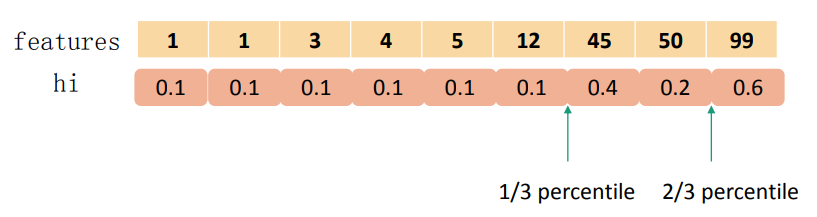
把目标函数整理成以下形式，可以看出 h_i 有对loss加权的作用:

3.1.5 LightGBM

LightGBM速度更快,内存占用更低,准确率更高(优势不明显，与XGBoost相当).

(1)直方图算法

把连续的浮点特征值离散化成k个整数，同时构造一个宽度为k的直方图。在 遍历数据的时候，根据离散化后的值作为索引在直方图中累积统计量，当遍 历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍 历寻找最优的分割点,如下图：

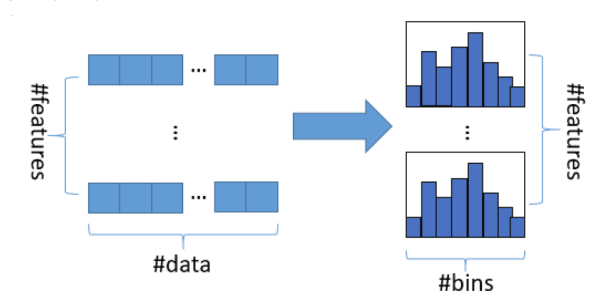
当离散为256个bin时，只需要8bit，比原始的浮点数节省7/8的内存占用。并 且减小了分裂时计算增益的计算量。

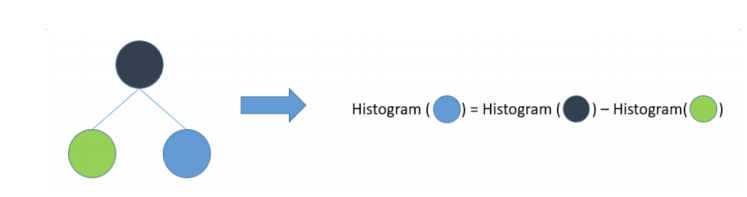
(2)直方图差加速

一个叶子的直方图可以由它的父亲节点的直方图与它兄弟节点的直方图做差得到，提升一倍速度,如图：

• 带深度限制的Leaf-wise的叶子生长策略

• 直接支持类别特征

• Cache命中率优化

• 多线程优化

参考

1. 李航 《统计学习方法》
2. 周志华 《机器学习》
3. 第06章：深入浅出ML之Boosting家族
4. 提升树GBDT详解
5. 梯度提升树(GBDT)原理小结
6. 『机器学习笔记 』GBDT原理-Gradient Boosting Decision Tree
7. 机器学习算法系列（7）：GBDT
8. xgboost 算法原理
9. xgboost中的数学原理
10. 树模型(六)：XGBoost
11. Xgboost论文